過度擬合在（overfitting）機械學習中是非常常見的問題，尤其是對於像類神經網路這樣具有許多可調參數（hyper-parameter）的大型模型。

到底什麼叫做過度擬合呢？在這裡我們需要先了解，訓練資料和機械學習之間的關係：這之間的關係可以用兩個 metrics 來描述，bias 和 variance。

在數學式上，我們可以對 mean squared error loss 做 partition，而分解出兩個不同的 terms：第一個 term 被稱為 bias 誤差，而第二個 term 則被稱為 variance 誤差。撇開數學式不談，高 bias 誤差通常是因為模型的能力（capacity）不足，未能正確描述訓練資料的平均分佈所造成，此時我們可稱為該模型為擬合不足（underfitting）。在這種情況下，增加訓練實例，並不會提高訓練模型的 performance，唯有增加模型的複雜度方能獲得較佳的 performance。

而高 variance 則是一個完全相反的情況，起因於過度複雜的參數模型，而導致模型過度記憶訓練實例的模式，而失去 generalization 的能力，也就是大家所熟知的過度擬合（overfitting）。在這種情況下，增加訓練資料或降低模型複雜度都會幫助減緩 overfitting 的情況。

在量測模型是否過度擬合或擬合不足，可以繪製一張模型 performance 和訓練資料大小的關係圖，這個關係圖又叫做 learning curve。在 Learning curve 圖中的 y 軸通常為 loss function，愈佳的訓練模型應該有較小的 loss，而 x 軸則繪製逐步增加的 training set size。

模型的 performance 必須要以 validation set 的 metrics 為主，因為對模型而言，training set performacne 總是和訓練資料的大小成正比，直到模型本身能力達到飽和，無法對額外增加的訓練資料擁有多餘的辨識能力。唯有量測 validation set 和 training set 的 performance 差距，才能準確的評估模型 generalization 的能力。

要注意的是，在繪製 learning curve 時 validation set size 並不會更動，那也就是為何在 learning curve 的一開始，validation error curve 與 training error curve 呈現一個相反的趨勢。因為，在小 training set 時，模型所學到的實例不足，尚未捕捉資料原分佈情況，所以 validation error 較大，然而隨著 training set 的 size 增加，模型所捕捉到的資料變異性愈多， validation error 則下降。

圖一和圖二是重新將吳恩達教授在 Coursera 教授的 Machine Learning 課程中，關於如何評估模型以及如何從 learning curve 診斷目前的模型是屬於 high bias 或 high variance。在此模型，用一個 polynomial 方程式來建立的迴歸模型的 Learning curve 。圖一和圖二的左圖中，loss function， J， 所計算出的 error，畫於縱軸，下標標註為 train 的 curve 是依據 training set size 的增加，而繪製的 training error curve，而下標標註為 cv 或 test 的 curve 是依據 validation set 所繪製的。

而圖一和圖二的右圖中，則是描述 polynomial 模型在做迴歸分析時的情況。右圖上，是以較少的資料點數來訓練模型，右圖下，則增加訓練資料點數，來訓練模型，可以看到在 high variance 的情況下，增加訓練資料點數，有助於降低模型的訓練誤差。

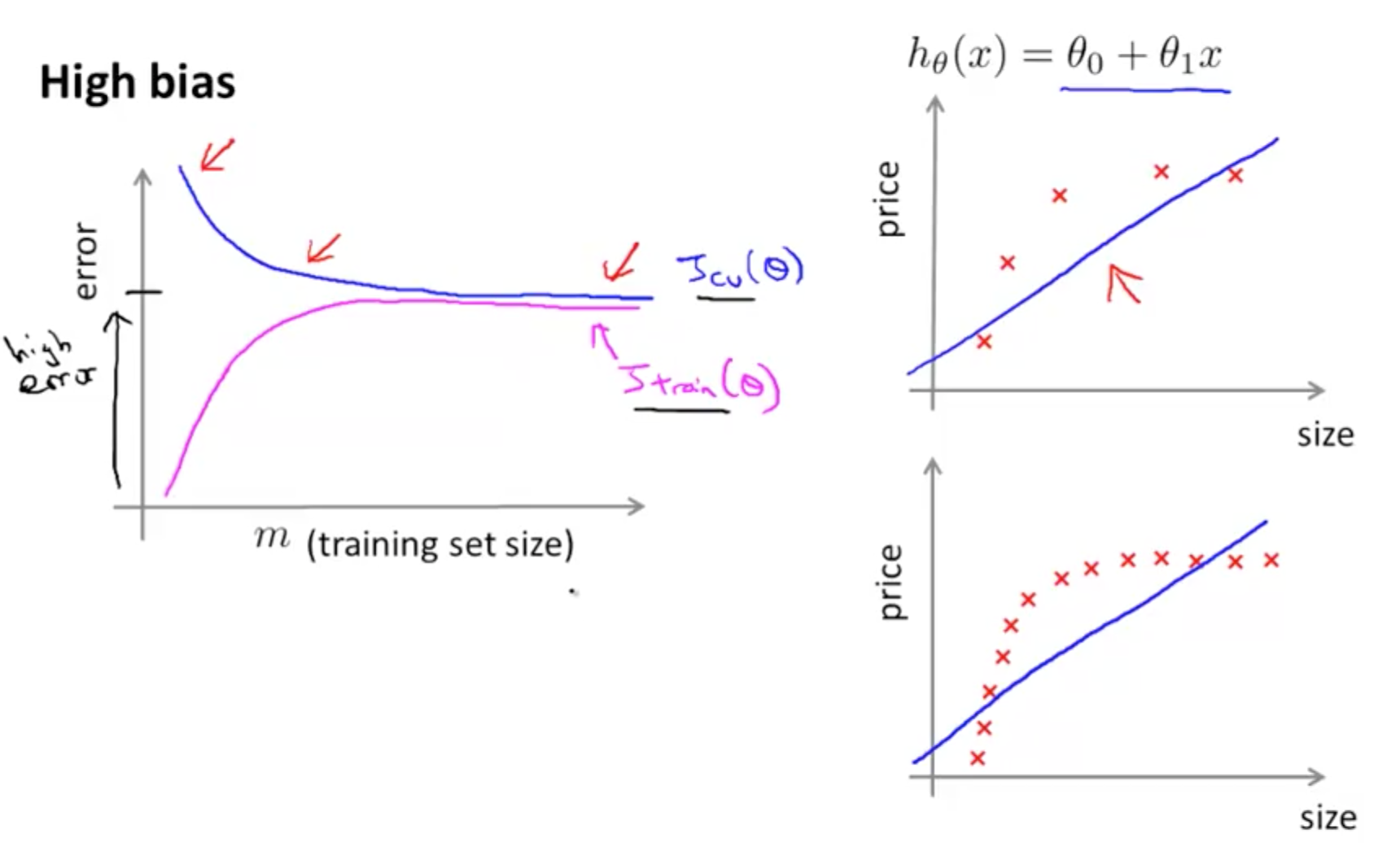
圖一：模型為 high bias 的情況，所繪製出來的 learning curve。可以看到無論 training set size 如何增加，validation error curve (藍紫色曲線) 和 training error curve (桃紅色曲線)都擁有相當小的差距。然而，因為 training error 即使在訓練資料少量的情況，便持續保持著較高的誤差值，所以可以斷定這是一個 high bias 的情況。

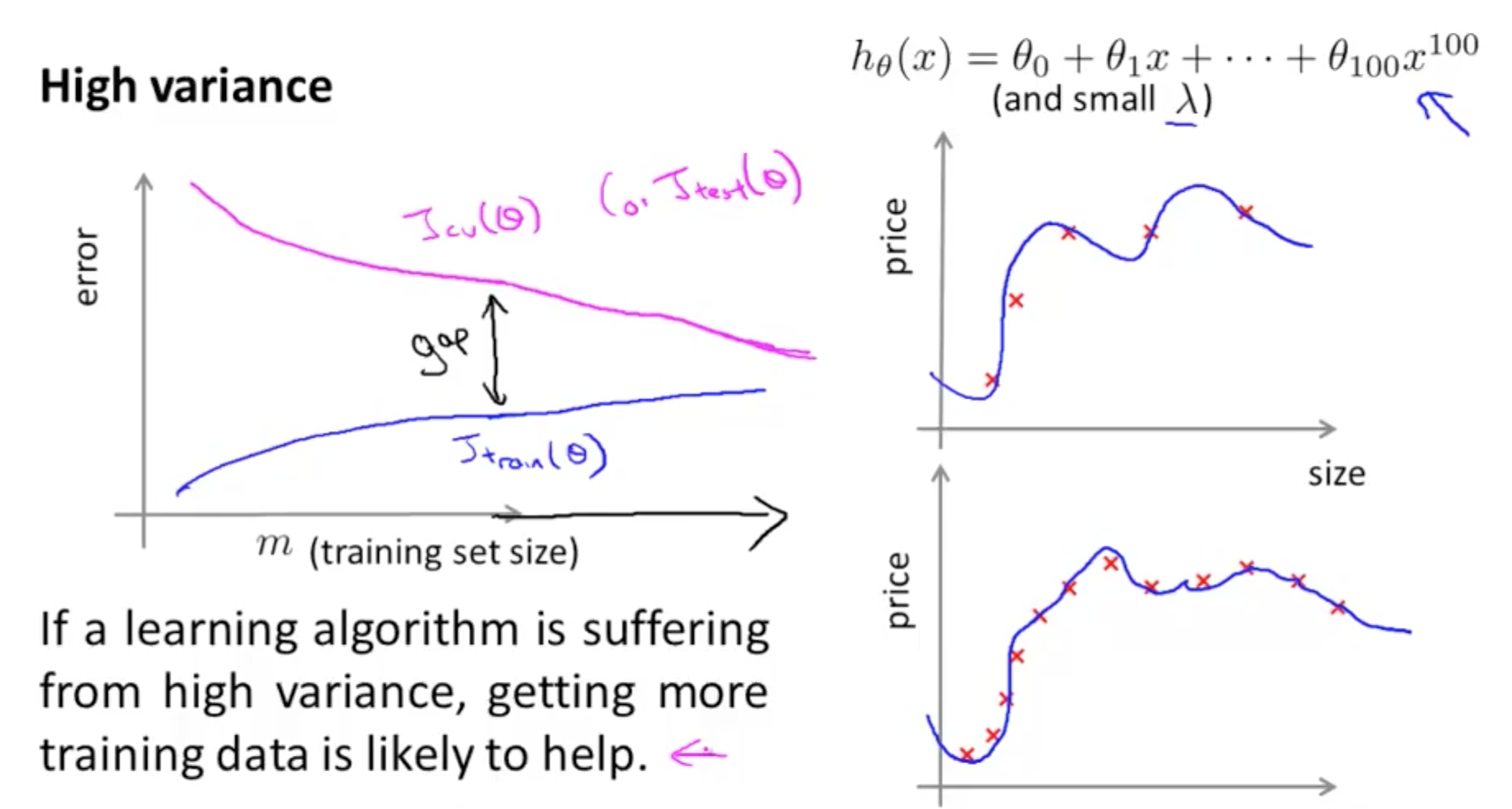
圖二：模型為 high variance 的情況，所繪製出的 learning curve。可以看到 training error curve （藍紫色曲線）隨著訓練資料的增加，training error 小幅度的增加，並且花較長的時間達到飽和，或接近飽和，所以這不是一個 high bias 的情況。然而，若觀察 validation error curve，雖然也隨著 training size 的增加下降，但始終和 training error curve 保持一個相當高的誤差，所以我們可以判定，這是一個 high variance 的情況。

一個不具有 high variance 或 high bias 的模型，其 learning curve 的特性，需要有較小的 training error 極限值， training error curve 隨著 training set size 擁有較緩和的 error increasing rate （或較小的 slope），以及和 validation curve 有較小的差距。

在解決擬合不足的情況下最簡單的方法就是增加模型的複雜度，在過度擬合的解決方案中，則有較多的討論包括加入 penalty term 到 loss function 內， 以及利用 ensemble 的方法來完成。在這裡我們僅討論在線性模型中常用的 penalty 方法，在這個方法中所有參數值，會以函式映射其各參數值的強度（不考慮方向）到一數值，此映射出的數值為正，會增加不含 penalty 的 loss function 的值。這個 penalty 輸出會乘上一個正的數值參數來作為控制 penalty 的強度，這個 penalty term 通常又被稱為 regularization term，而其映射的方式最常用的為 l2 和 l1 norm penalty。

上圖中，第一個數學式是在原本的 loss function (L(x, y, w)) 中加入了 Regularization term。而這個 Regularization term 可以用 l1 norm （左）和 l2 norm （右）來作為 penalty。

在 l1 norm 與 l2 norm 下面的圖形，則是一個用二維（兩個參數值，W1 和 W2）對 regularization 的原理做簡單的說明。可以想像，這個圖是 3D 圖形的二維截面圖，右上方如等高線般的圓形圖，則是原本 loss function (unregularized) 的二維截面。在 l1 norm 的 regularization term 會對權重空間，繪出一個如菱形的圖形（因為是 W1 和 W2 的線性組合，又因為取絕對值，而造成上下左右對稱）。而加入 l1 norm regularization term 後，與原本 loss 相交且總和為最小的情況，發現 W1 為零的情況可以達成。（y 軸，w* 的點）

同樣的 l2 norm 會造成一個圓形（右），但最佳 loss 的狀況則是靠近 W1 為零的地方。

另外，我們也可以使用 Tensorflow 的視覺化圖形介面套件 Tensorboard 來對學習到的各種統計參數做事覺化診斷。要使用 Tensorboard 必須要啟動另外一個 local server，並且給予這個 Server ，訓練模型以 checkpoints 檔案格式將模型 export 到指定的硬碟位置。在這個資料夾中，由 tf.estimator API 建構的 Estimator 物件會定期的將訓練好的模型輸出到這個位置下的資料夾，以及一些由使用者定義的關於描述模型能力的統計值，透過 tf.summary 的方法記錄成 event files 格式，存在指定的資料夾中。

關於如何使用 API 呼叫對應的方法來進行模型輸出合統計值紀錄，在 tf.estimator API 中都已經幫使用者寫好，使用者想要客製化這些行為可以透過在建立模型的物件時，自行提供一個 tf.estimator.RunConfig 物件，並輸入與預設值不同的設定。參數的說明可見 tf.estimator.RunConfig 物件的 API。

在下一篇中，我們將要稍微把鐵達尼模型擱在一旁，深入地來看看 Tensorflow 的程式架構。

圖片來源：

1. 圖一和圖二：來自於新加坡的 Ritchieng.com 筆記
2. 圖三來自於What is Regularization in Machine Learning?