前言

昨天提到策略增進，是一個使用計算出的狀態價值，去選擇在每個狀態下，最好的動作的方法。其中，我們在選擇動作時，使用動作價值函數計算動作價值，並使用動作價值最高的動作，作為這個狀態下最好的動作。

策略迭代 (Policy Iteration)

透過狀態價值，我們找到每個狀態下最好的動作。那麼，用這個動作再回去計算狀態價值，我們就可以得到更準確的狀態價值。重複這個過程的話，最終我們可以逼近各狀態的價值 (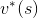)，與各狀態下最適合的動作 ()。

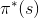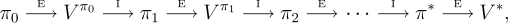(取自 Sutton 書籍)
上圖中重複的過程，就是我們上述「計算狀態價值」與「各狀態最適動作」。以下是這個方法的演算法：

以下一邊介紹演算法的內容，一邊說明相關的程式碼。

• Step 1 - Initialization
  設定動作、狀態價值函數、獎勵函數、轉移矩陣...等內容，還有演算法中會使用到的參數。

## environment setting
# action
BestAction = np.random.randint(0,4,16)
ProbAction = np.zeros([16,4])
ProbAction[1:15,:] = 0.25
# value function
FuncValue = np.zeros(16)
# reward function
FuncReward = np.full(16,-1)
FuncReward[0] = 0
FuncReward[15] = 0
# transition matrix
T = np.load('./gridworld/T.npy')

gamma = 0.99
theta = 0.05
counter_total = 0
PolicyStable = False

• Step 2 - Policy Evalution
  即之前計算狀態價值的方法，為方便之後使用，將這個東西定義成 function。

def PolicyEvalution(func_value, best_action, func_reward, trans_mat, gamma):
    func_value_now = func_value.copy()
    for state in range(1,15):
        next_state = trans_mat[:, state, best_action[state]]
        future_reward = func_reward + func_value_now*gamma
        func_value[state] = np.sum(next_state*future_reward)
    delta = np.max(np.abs(func_value - func_value_now))
    return func_value, delta

• Step 3 - Policy Improvement
  選擇每個狀態下最好的動作，一樣定義為 function 方便使用。

def PolicyImprovement(func_value, best_action, prob_action, func_reward, trans_mat, gamma):
    policy_stable = False
    best_action_now = best_action.copy()
    for state in range(1,15):
        prob_next_state = prob_action[state]*trans_mat[:,state,:]
        future_reward = func_reward + func_value*gamma
        best_action[state] = np.argmax(np.matmul(np.transpose(prob_next_state), future_reward))
    if np.all(best_action == best_action_now):
        policy_stable = True
    return best_action, policy_stable

• Run in while
  我們需要重複上面 Step 2 與 3 的內容，直到我們的最佳動作已經不再改變 (程式中的變數為 PolicyStable)。

def main():
    ## environment setting
    # action
    BestAction = np.random.randint(0,4,16)
    ProbAction = np.zeros([16,4])
    ProbAction[1:15,:] = 0.25
    # value function
    FuncValue = np.zeros(16)
    # reward function
    FuncReward = np.full(16,-1)
    FuncReward[0] = 0
    FuncReward[15] = 0
    # transition matrix
    T = np.load('./gridworld/T.npy')

    # parameters
    gamma = 0.99
    theta = 0.05
    counter_total = 0
    PolicyStable = False

    # iteration
    while not PolicyStable:
        delta = theta + 0.001
        counter = 1
        counter_total += 1
        while delta > theta:
            FuncValue, delta = PolicyEvalution(FuncValue, BestAction, FuncReward, T, gamma)
            counter += 1
        os.system('cls' if os.name == 'nt' else 'clear')
        ShowValue(delta, theta, gamma, counter_total, counter, FuncValue)
        time.sleep(2)
        BestAction, PolicyStable = PolicyImprovement(FuncValue, BestAction, ProbAction, FuncReward, T, gamma)
        PolicyString = ShowPolicy(counter_total, BestAction)
        time.sleep(2)

    os.system('cls' if os.name == 'nt' else 'clear')
    print('='*60)
    print('Final Result')
    print('='*60)
    print('[State-value]')
    print(FuncValue.reshape(4,4))
    print('='*60)
    print('[Policy]')
    print(PolicyString.reshape(4,4))
    print('='*60)

這個部分的內容包含 Step 1 中設定的參數，並設定迴圈的中止條件。經過四次「計算狀態價值」與「選擇最佳動作」的過程，我們得到結果如下： ('*'為終點，尖端為最佳移動方向)

============================================================
Final Result
============================================================
[State-value]
[[ 0.    0.   -1.   -1.99]
 [ 0.   -1.   -1.99 -1.  ]
 [-1.   -1.99 -1.    0.  ]
 [-1.99 -1.    0.    0.  ]]
============================================================
[Policy]
[['*' '<' '<' '<']
 ['^' '^' '^' 'v']
 ['^' '^' 'v' 'v']
 ['^' '>' '>' '*']]
============================================================

以上，我們完成使用 Policy Iteration 進行決策，完整程式碼請見 GitHub。