前言

昨天我們提到 Eligibility Traces，透過這個東西以及 TD Learning，推論出新的估計狀態價值方法 TD()。今天將回到使用梯度下降法，更新逼近函數的參數一事。

參數更新方法

昨天我們使用的 TD()，其狀態價值更新方法如下：

在上式中，中括弧內部指出我們「估計狀態價值的誤差」，並以此為更新依據。在函數逼近法中更新參數時，除了誤差我們還需要知道更新方向，因此需要將上式加上梯度，如下所示：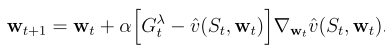

因此昨天實作上使用的參數，也需要做一些修正。

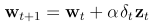
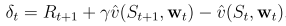
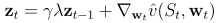
整體流程如下：

實作

實作的部分，一樣以 GridWorld 為例，並分成以下的函數：

• ValueFunction (價值近似函數)
• SimProc (模擬過程)
• Update (更新權重、trace)
• Gradient (計算梯度)
• PrintValue (呈現狀態價值)
• main (主程式)

我們呈現「價值近似函數」與「更新權重、trace」的函數，完整內容請參考 GitHub

• ValueFunction

def ValueFunction(state, weights):
    state_array = np.zeros([1,16])
    state_array[:, state] = 1
    value = np.matmul(state_array, np.transpose(weights))
    return value

自定義的價值近似函數，方程式如下：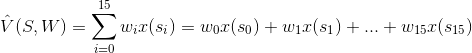

這種定義方法與原本使用表格法的方法接近，這邊用這種定義方式方便理解，也可以自己設計其他的價值近似函數，例如：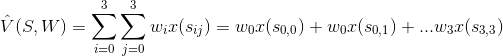

• Update (更新權重、trace)

def Update(weights, trace, records, alpha, gamma, trace_lambda):
    state = records[0]
    aciton = records[1]
    reward = records[2]
    next_state = records[3]
    # update value, trace, and state
    delta = reward + gamma*ValueFunction(next_state, weights) - ValueFunction(state, weights)
    trace = gamma*trace_lambda*trace + Gradient(state)
    weights += alpha*delta*trace
    return trace, weights

相較於昨天的使用表格的方式記錄 trace，在近似價值函數中並不需要。

執行結果

經過 200 episodes 後，我們得到以下的結果

============================================================
[State-Value]
Episode: 200
[[  0.          -7.99060454 -12.75388735 -13.29202159]
 [ -9.94611435 -11.45644001 -12.51934095 -11.87256793]
 [-12.81091065 -12.71606135 -11.28626883  -8.44567188]
 [-12.89114835 -12.428723    -9.65360567   0.        ]]
============================================================

至此，我們完成使用近似函數進行狀態價值估計。動作價值估計的方法與狀態價值估計接近，在此不多做說明，有興趣可以參考 Sutton 書籍的 Chapter9。

其他方法

這邊簡單說明其它沒有介紹的方法，例如

• 調整輸入

  • Coarse Coding
  • Radial Basis Function
  • Kanerva Coding
    針對輸入的數值進行調整，讓線性模型可以處理更複雜的問題。

• 非線性模型

  • Neural Network
    因為計算能力變強，所以開始流行的方法。

• Policy Approximation

  • 不再單純使用動作價值與 -greedy 決定最佳策略，也建構選擇動作的機制。

在這個領域中，還有許許多多的方法，就請自己去找想要探索的地方吧！