前言

昨天總結了 TD Learning 的方法，截至目前為止，我們介紹了許多估計價值的方法。不過所有的方法，我們處理的狀態都是離散的，不論是 GridWorld 還是 Cliff-Walking。那麼，如果我們遇到的狀態不是離散的，要怎麼處理這樣的問題呢？

Tabular Method

現在我們解決的問題，以及使用的方法，都是使用表格法處理的。怎麼說呢？在我們目前討論過的方法中，不論是狀態價值或是動作價值，都使用矩陣紀錄該 狀態 或是該 狀態-動作 的價值。

可能會有人有疑問，「連續狀態的情況，還是可以把狀態簡化成離散狀態，繼續使用表格法」。這個想法並沒有問題，然而問題在於，這樣簡化後會有無限的狀態，我們不可能記錄所有狀態的價值，更不用說這些狀態的動作價值。

因此，如果我們要解決這個問題，從根本上的方法是「不要再使用表格紀錄價值」，那麼我們應該怎麼估計價值呢？說起來很簡單，使用函數逼近就好了。

• 說起來很簡單，但做起來就不一定了。
• 其實之前在陳述狀態價值時，有時會筆誤成狀態價值函數，原因是因為大多的方法已經不用表格記錄，而是使用函數逼近，這種情況下的狀態價值會由 狀態價值函數 估計。(這絕對不是在幫自己的筆誤找藉口)

Function Approximation (函數逼近)

我們可以使用一條函數來逼近狀態價值以及動作價值，這條函數可以是線性的，也可以是非線性的。在方法上也有許多，在 Sutton 的書中，光是線性方法就有四種：

• Coarse Coding
• Tile Coding
• Radial Basis Functions
• Kanerva Coding

而非線性的部分，最耳熟能詳的方法就是神經網路了，前陣子很紅的 alpha-GO 所使用的 DQN，就是使用神經網路作為狀態價值函數以及動作價值函數的 Q-Learning 方法。

好的，先不管用什麼方法逼近狀態/動作價值，之前在更新價值時，是針對表格的數值更新。可是現在沒有表格了，因此要更新會影響函數的東西，那個東西就是函數的參數。假設現在有一個多項式函數：

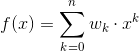
想要使用迭代更新函數的參數 w，使得狀態函數 f(x) 與真實值的差異最小。這種找最大最小值 (以下稱為極值) 的更新參數方法，最容易想到的就是梯度下降法了。不過不能預設每個人都知道，所以從梯度開始說明。

梯度 (Gradient)

假設現在有一個函數 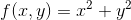那麼我們可以定義這個函數的梯度為 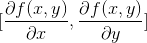，記作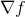

太快了嗎？那我們回頭看看微積分。如果我現在要找一個二次函數的極值，是不是找到切線斜率等於 0 的地方，那裏就有存在極值。而梯度，可以想成高維空間的斜率，當找到梯度等於 0 的地方，那裏也存在極值。只是在這裡可能有很多參數，所以不能只計算微分找一個維度上的 "斜率"，要計算偏微分找每個維度上的 "斜率"。

梯度下降法 (Gradient Method)

梯度下降法是一種使用梯度，幫我們找到極值的方法。假設現在有一條二次函數曲線 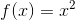，我想要透過迭代不斷更新 x 找到函數的最小值。可以使用

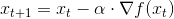
其中，

• t 表示第幾次迭代
• 一樣是學習率 (從誤差更新多少)
• 實作如下

import numpy as np
import matplotlib.pyplot as plt

# function
def func(x):
    return np.power(x,2)

# gradient
def dfunc(x):
    return 2*x

# gradient descent
def GD(x_start, alpha, threshold):
    trajectory = [x_start]
    x = x_start
    update = float('Inf')
    while abs(update) > threshold:
        dx = dfunc(x)
        update = -dx*alpha
        x += update
        trajectory.append(x)
    return trajectory

# main
x = GD(2, 0.03, 0.001)

# plot
t = np.arange(-3, 3, 0.01)
plt.plot(t, func(t), color = 'b')
plt.scatter(x, func(x), color = 'r')    
plt.show()

• 結果圖
  

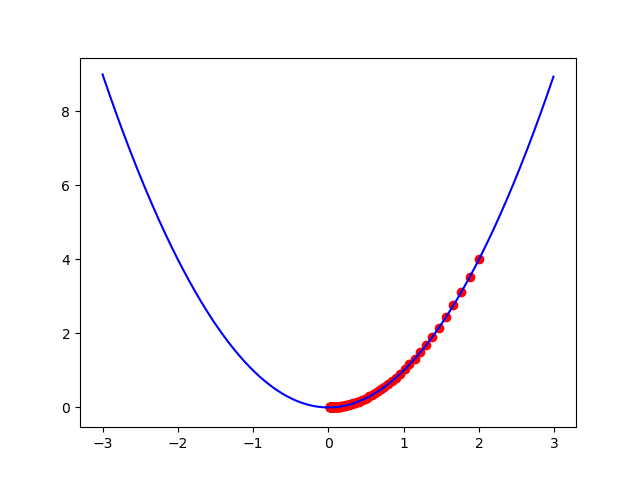
好的，現在我們有迭代更新參數的方法了。不過在說明怎麼在強化學習上使用梯度下降法之前，還需要知道一個東西，稱為「Eligibility Traces」，明天將會說明這個東西。