前言

昨天提到要使用函數逼近的方式代替原本的表格法，並說明可以使用梯度下降法更新價值，但在說明價值之前，要在介紹一個稱為 Eligibility Traces，今天將會介紹這個東西。

Eligibility Traces

TD-Learning 與 Monte Carlo

在介紹 Eligibility Traces 之前，先來了解為什麼數學家會想出這樣的東西。回頭看看 TD-Learning 與 Monte Carlo 的方法，這兩個方法其實是更新方法的兩種極致。

• TD-Learning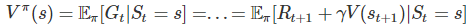
  
  只使用一個回饋進行更新。

• Monte Carlo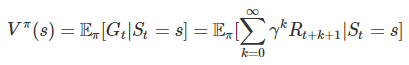
  
  使用所有的回饋進行更新。

數學家想要找一個折衷的方法，所以提出了 n-step TD prediction

n-step TD prediction

這是一個針對 作文章的方法，將原本 TD-Learning 的價值估計寫作

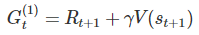
再多寫出兩個回饋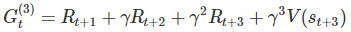

寫成泛用的形式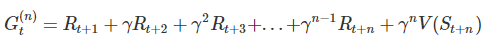

因此我們可以把更新價值的方法，改用這個形式計算：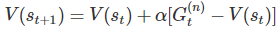

TD()

不過這裡有一個問題，我們到底應該把 n 設為多少才是適當的呢？數學家很貪心，覺得需要每個都來一點 (我全都要)，所以定義了下面這條式子：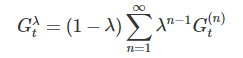
其中

但是每個 episode 都有結束的時候，所以上述使用無限表示不太好，假設 episode 在 t = T 時結束，可以將上式改寫為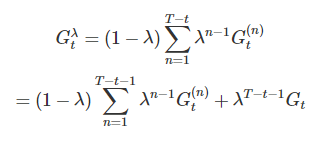

這邊使用一個例子幫助理解，並說明這個式子的一些特性。假設 t=0、T=3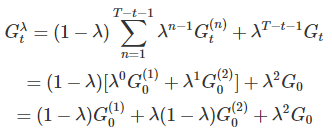

其中有幾個地方要注意

• 所有的係數相加為 1

  

• 使用所有可能的 進行評估，當 越大，傾向觀察越多 reward 的設計 (ex: )；相反的 越小，傾向觀察越少 reward 的設計 (ex: ) 。

使用這個形式，可以在將價值更新的方法改寫為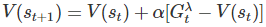

實作

說明完這個方法要開始實作時，突然意識到一個問題。之前使用 Monte Carlo 方法更新時，需要一個 episode 完成後才更新，那現在也需要這樣嗎？

答案是不用，因為數學家已經想到使用在 episode 內，依然可以更新的方法了，那個關鍵就是 Eligibility Traces。

不講我都忘記大標是這個了...

使用這個東西，紀錄曾經經過的地方，並在更新時調閱這個紀錄，流程如下：

在流程中有一個沒看過的 Z(s) 表格，也就是 Eligibility Traces。每當經過某個狀態時，表格就會記錄曾經經過這個狀態 (Z(S) = Z(S) + 1)，並在更新時適度衰退。

實作內容中包含：

• SimProc (模擬過程)
• Update (更新價值與 Trace)
• PrintValue (呈現狀態價值)
• main (主程式)

因為主要內容在 Day 22 已經說明了，以下將只呈現 Update

def Update(state_value, state_trace, records, alpha, gamma, trace_lambda):
    # calculate value update
    state = records[0]
    action = records[1]
    reward = records[2]
    next_state = records[3]
    delta = reward + gamma*state_value[next_state] - state_value[state]
    # update trace matrix
    state_trace[state] += 1
    # update state-value and decay trace
    state_value += alpha*delta*state_trace
    state_trace = gamma*trace_lambda*state_trace
    return state_value, state_trace

相較於 Day 22 簡短的 GetValue，這裡多計算了 delta 以及更新 trace。另外在使用 trace 時，需要額外設定參數 (trace_lambda)，這邊在測試時使用 = 0.5，僅 500 episodes 就獲得與 Day 22 - 1000 episodes 類似的結果，完整程式內容。

[2018/11/14 更新] 發現程式內容錯誤，修改實驗結果。

實驗結果

============================================================
[State-Value]
Episode: 500
[[  0.          -8.02864214 -14.80443492 -16.62307602]
 [-10.40612339 -12.47010784 -14.97857654 -14.56262576]
 [-15.8437244  -14.55221974 -13.35310022  -8.41472618]
 [-16.66272462 -14.04768217  -9.78038944   0.        ]]
============================================================

由結果得之，使用更多的回饋於價值估計上，可以有效的提升效率。現在我們知道 Eligibility Traces 是什麼，以及它的用途，明天將會回到說明使用梯度下降法 逼進函數 (Approximation function) 更新參數的方式。