在學習隨機森(Random Forest)前先了解一下邏感知器(Perceptron)，因為後面複雜的演算法的原理都從它來。
參考網站1參考網站2

感知器 Perceptron

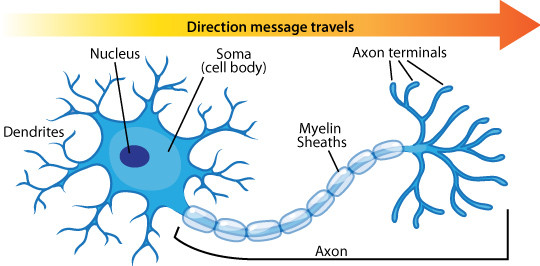
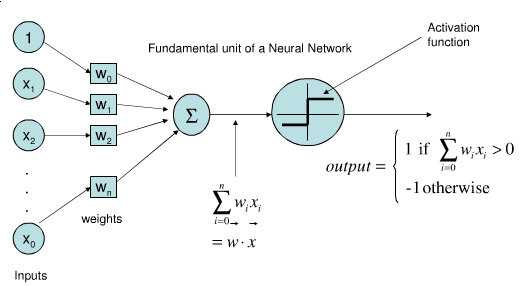
從上圖可了解感知器就是類比神經元的運行方式，有input端結合權重加總後再傳到activation function去決定分成哪一類，但Perceptron在資料是線性可分割的情況下演算才會停止如下左圖。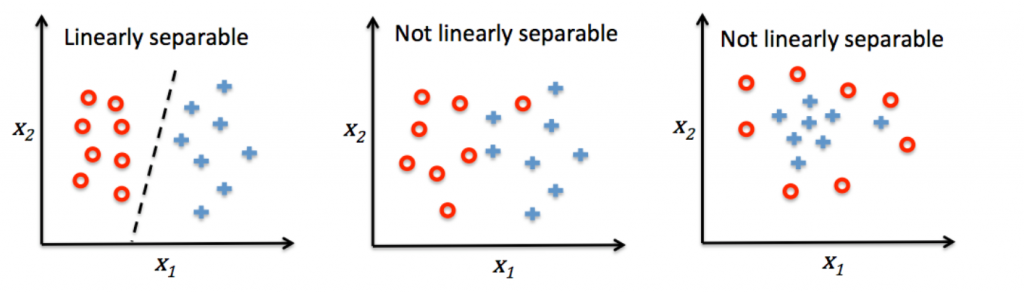

我們假設input有兩個特徵值輸入x1,x2乘以各自權重w1,w2相加後如果大於或小於某個值就會被activation function分成兩類。例如x1w1+x2w2>０ 是 +1 ，0< 是 -1，train model就是再找到好的權重w1,w2能將資料做好分類。接下來就用下圖Iris dataset資料集來了解，究竟是怎麼找到的權重與某個定植～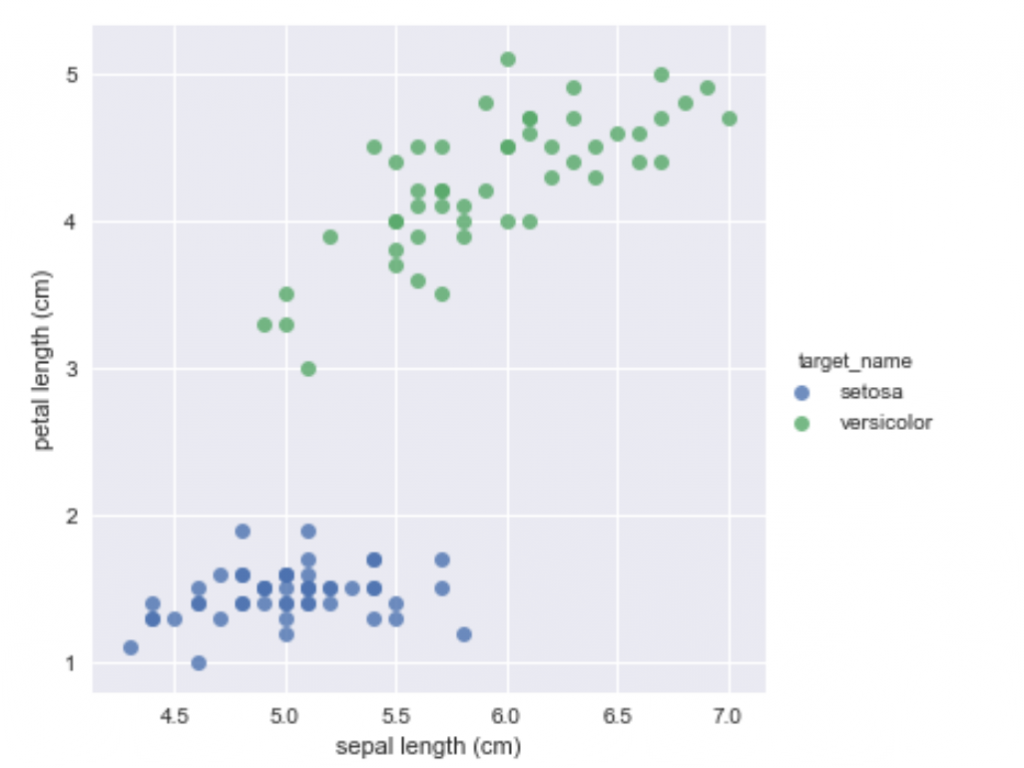

from sklearn import datasets
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
iris = datasets.load_iris()
x = pd.DataFrame(iris['data'], columns=iris['feature_names'])
print("target_names: "+str(iris['target_names']))
y = pd.DataFrame(iris['target'], columns=['target'])
iris_data = pd.concat([x,y], axis=1)
iris_data.head(3)
iris['target_names']
target_name = {
    0:'setosa',
    1:'versicolor',
    2:'virginica'
}
iris_data['target_name'] = iris_data['target'].map(target_name)
iris_data = iris_data[(iris_data['target_name'] == 'setosa')|(iris_data['target_name'] == 'versicolor')]
iris_data = iris_data[['sepal length (cm)','petal length (cm)','target_name']]
iris_data.head(5)
target_class = {
    'setosa':1,
    'versicolor':-1
}
iris_data['target_class'] = iris_data['target_name'].map(target_class)
del iris_data['target_name']
def sign(z):  # 定義激勵函數activation function
    if z > 0:
        return 1
    else:
        return -1
        
w = np.array([0.,0.,0.])
error = 1
iterator = 0
while error != 0:
    error = 0
    for i in range(len(iris_data)):
        x,y = np.concatenate((np.array([1.]), np.array(iris_data.iloc[i])[:2])), np.array(iris_data.iloc[i])[2]
        if sign(np.dot(w,x)) != y:
            print("iterator: "+str(iterator))
            iterator += 1
            error += 1
            sns.lmplot('sepal length (cm)','petal length (cm)',data=iris_data, fit_reg=False, hue ='target_class')
            
            # 前一個Decision boundary 的法向量
            if w[1] != 0:
                x_last_decision_boundary = np.linspace(0,w[1])
                y_last_decision_boundary = (w[2]/w[1])*x_last_decision_boundary
                plt.plot(x_last_decision_boundary, y_last_decision_boundary,'c--')
            w += y*x            #最重要的一行負責更新權重w
            print("x: " + str(x))            
            print("w: " + str(w))
            # x向量 
            x_vector = np.linspace(0,x[1])
            y_vector = (x[2]/x[1])*x_vector
            plt.plot(x_vector, y_vector,'b')
            # Decision boundary 的方向向量
            x_decision_boundary = np.linspace(-0.5,7)
            y_decision_boundary = (-w[1]/w[2])*x_decision_boundary - (w[0]/w[2])
            plt.plot(x_decision_boundary, y_decision_boundary,'r')
            # Decision boundary 的法向量
            x_decision_boundary_normal_vector = np.linspace(0,w[1])
            y_decision_boundary_normal_vector = (w[2]/w[1])*x_decision_boundary_normal_vector
            plt.plot(x_decision_boundary_normal_vector, y_decision_boundary_normal_vector,'g')
            plt.xlim(-0.5,7.5)
            plt.ylim(5,-3)
            plt.show()

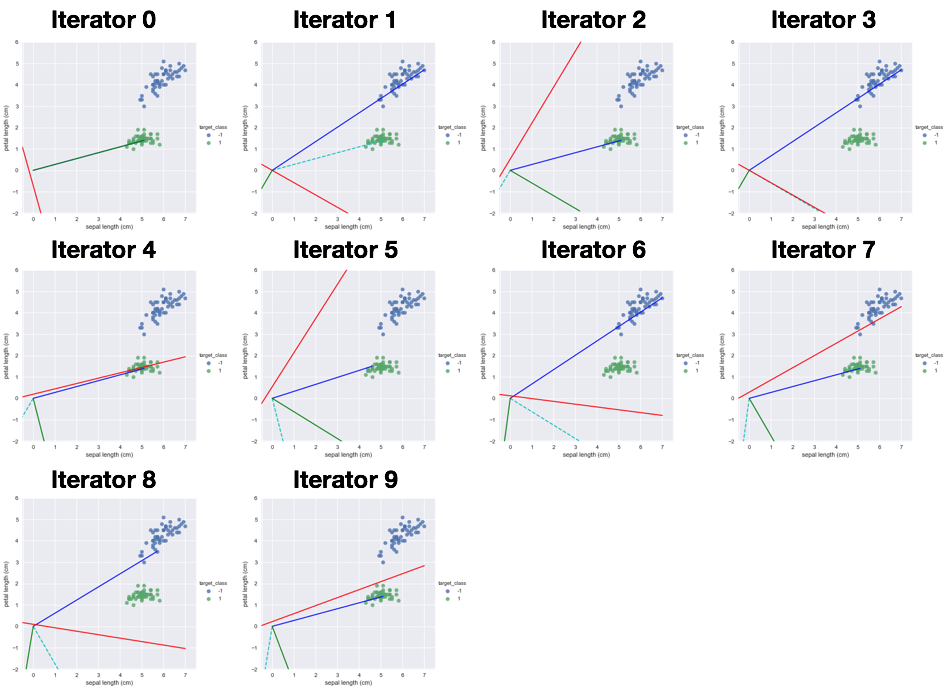
從上流程了解感知器的修正過程，它的原理可以推廣到更複雜的演算法像是深度學習也是。但Perception也是有缺點的如開頭所說要線性可分，而且只知道結果是哪一類AorB，無法知道是A機率多少或B的機率多少。明天要來學習邏輯斯回歸(Logistic regression)可以知道機率是說少～