為什麼今天練習這個呢？

在生物資訊領域裡頭其實有非常多的工具或是演算法都是用Hidden Markov Model (HMM)去實作的，但不才我因為生性懶散，所以過去我在這一部份也僅僅只是知其然，而對於其所以然的部份所花心思甚少。現在既然在學這個宣稱是最適合科學計算使用的語言Julia，那就要好好地熟悉一下怎麼使用裡頭的數學工具，而最好的方法就是拿來實作HMM裡頭一個最簡單的Forward演算法啦！

由於這就是一個練習，所以我在此就不介紹HMM的原理了

我今天想要拿練習的範例是這樣的：

假設我現在手上有三個紙箱，分別標上箱子1、箱子2以及箱子3，而且每個箱子裡頭都裝滿了一定數量的紅色及白色兩種不同顏色的小球。現在我隨機在這三個箱子裡頭選一個箱子抽出一個小球，紀錄完球的顏色之後就將球放回原本的箱子裡。在抽了三次球之後，我紀錄到的顏色依序是紅、白、紅。

依據這個實驗，我想透過HMM來計算我抽到這樣的結果的可能性有多高，在隨便設定了幾個參數後，我的程式碼看起來像這樣：

#!/usr/bin/env julia
using LinearAlgebra

struct HMM
	transitionMat::Array{Float64, 2}
	emissionMat::Array{Float64, 2}
	initialProb::Array{Float64, 1}
end


function Forward(hmmObj::HMM, observation::Array, obsEvents::Array)
	obsEventsNum = length(obsEvents)
	N = size(hmmObj.transitionMat)[1]
	α = zeros(Float64, N, obsEventsNum)
	eventOrder = map(i -> (1:length(observation))[observation .== i][1], obsEvents)
	α[:, 1] = hmmObj.initialProb .* hmmObj.emissionMat[:, eventOrder[1]]
	for o = 2:obsEventsNum
		for n = 1:N
			α[n, o] = dot(α[:, o-1], hmmObj.transitionMat[:, n]) * hmmObj.emissionMat[n, eventOrder[o]]
		end
	end
	prob = sum(α[:, obsEventsNum])
	return prob, α
end

A = [0.5 0.2 0.3; 0.3 0.5 0.2; 0.2 0.3 0.5]
B = [0.5 0.5; 0.4 0.6; 0.7 0.3]
π = [0.2; 0.4; 0.4]
observation = ["red", "white"]
events = ["red", "white", "red"]

hmm = HMM(A, B, π)
prob, fp = Forward(hmm, observation, events)

println("\033[1;32mThe forward probability is:\033[0m")
display("text/plain", fp)
println("\n\n\033[1;32mProbability: \033[0m", prob)

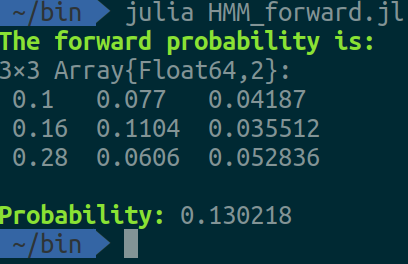
經過執行，會得到這樣的結果: