剛剛讀了一下之前的統計學，要了解Machine Learning的數學原理，除了線性代數、統計學、還有一點點工數，最近都在惡補的說(哀~)XD。
今天要來講解主成分分析(Principal Component Analysis)，他是一種非監督式(unsupervised)降維(Dimension reduction)的演算法，可以用來過濾雜訊、特徵擷取...等。

• 一樣先匯入今天要舉例的資料集以及使用的模組

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

• 首先，以亂數產生200個點，並呈現在二維平面中

rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal');

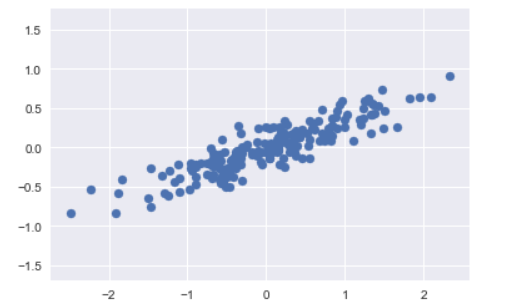
根據上圖輸出結果，可以看到，這200個亂數產生的點，在X軸、Y軸平面上呈現線性關係
而在主成分分析非監督式學習問題中，他是以學習X軸與Y軸的關係，並量化其關係；並非是由X軸的資料預測Y軸的資料。

• 匯入SKlearn中的PCA模組。n_components：要保留組件的數量

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)

可以用 pca.n_components_查看保留的組件數、 pca.explained_variance_ 解釋平方差

• 再來，定義draw_vector函數，我們要來預測資料的向量方向及平方長度

def draw_vector(v0, v1, ax=None):
    ax = ax or plt.gca()
    arrowprops=dict(arrowstyle='->',
                    linewidth=2,
                    shrinkA=0, shrinkB=0)
    ax.annotate('', v1, v0, arrowprops=arrowprops)

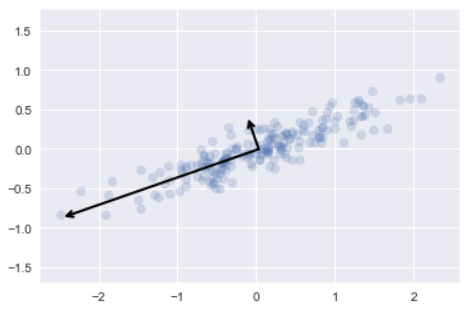
# plot data
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * 3 * np.sqrt(length)
    draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal');

• 要如何將資料數據降維呢?
  就是需要將一組或多組資料的主成分(principal components)歸零，

pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
print("original shape:   ", X.shape)
print("transformed shape:", X_pca.shape)

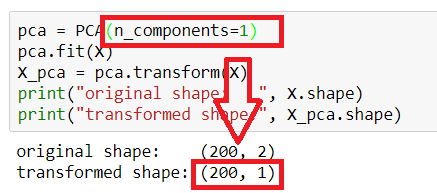
可以看到上圖，將transformed數據，轉換為單一維度

X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.3)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.7)
plt.axis('equal');

-
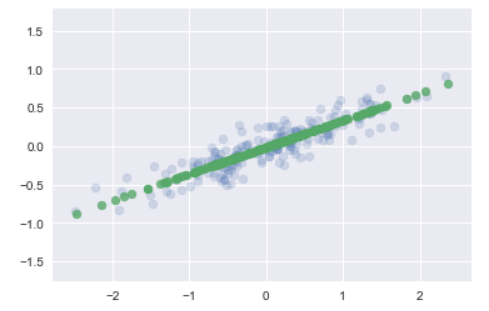
依據上圖輸出的結果，可以看到數據轉換為一維資料後去除雜訊，資料擬合至一條直線。