一早 Moore 與 Pete 就跟 Fields 抱怨昨天的 Linear Regression 程式跑到訓練就異常了
每個 Epoch 計算損失函數 NaN（Not a Number)。

epoch 1, loss nan
epoch 2, loss nan
epoch 3, loss nan

這個還在 Fields 預料之內，先請大家看一下程式中有印出面積與房價對應圖，觀察到面積分佈從10到50；對應房屋價格200萬到1200萬隨機分佈。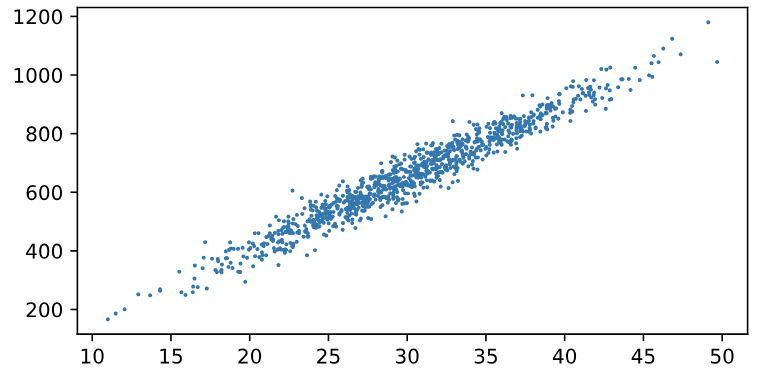

這需要做Feature scaling，讓訓練順利。請大家把一行程式稍微改一下：

features = nd.random.normal(loc=30, scale=6, shape=(num_examples, num_features))
#面積與屋齡兩者我們都簡單的用平均面積30坪或年 （loc=30）

改為

features = nd.random.normal(scale=6, shape=(num_examples, num_features))
#標準分配的中間值取預設值 0，這意味著房子平均屋齡接近0年。當然不合理。

結果如預期出現一些輸出：

epoch 1, loss 10.788737
epoch 2, loss 0.029127
epoch 3, loss 0.000053
…  …  …
true_w, w
([25, -6],     #我們假設的房價25萬元/面積；每年房價價值少 -6萬元
 [[25.000225]
  [-5.999537]]  #藉由機器學習 mini-Batch Gradient Descent 演算法找到很接近 [25, -6] 正確值。
 <NDArray 2x1 @cpu(0)>)  

true_b, b
(80,    #屋價的起始值 80萬元起跳
 [79.99011]  #演算法找到很接近 [80] 正確值。
 <NDArray 1 @cpu(0)>)

雖然只刪掉7個字元（loc=30,）就神奇可以完成預期結果。Moore 稍微看新的面積與房價對應圖，忍不住唸了Fields一下：”怎麼可能房屋有負數的年份，一堆 -15到0年屋齡的房子，還時間倒流ㄟ！要是我們真的收集到真實數據，難不成你要告訴我們必須竄改數據，機器學習才有用處？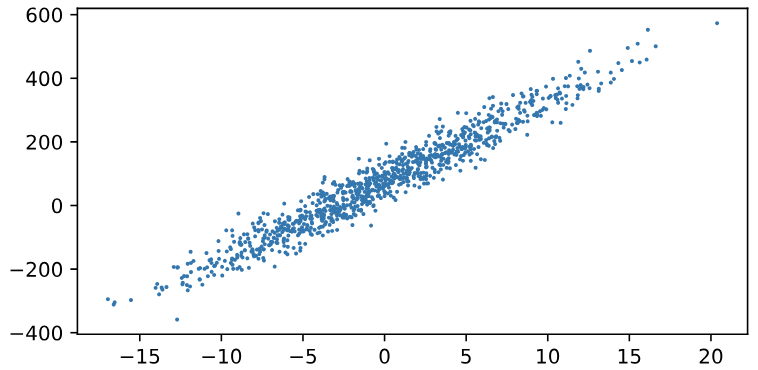

Pete幫忙解危："這個算簡單吧，我們實際解真實的數據，做了Feature scaling後再訓練出最佳化的參數後，等到要進行房價預測，也有人叫做推理或推論 (inference)，就把值反向放大縮小與平移不就得了！馬上寫一個給你看看："

rawFeatures = nd.random.normal(loc=30, scale=6, shape=(num_examples, num_features))
rawLabels = true_w[0] * rawFeatures[:, 0] + true_w[1] * rawFeatures[:, 1] + true_b 
rawLabels += nd.random.normal(scale=8, shape=rawLabels.shape)

def LXnorm(ndar):  #將數據平移，平均值變成0
    mean=nd.mean(ndar,axis=0)
    return mean,ndar-mean

meanF, features=LXnorm(rawFeatures) 
meanL, labels=LXnorm(rawLabels)

另外 Molly 看到幾行與一般程式作法不太一樣，同時也沒有看到先前計算偏微分的導數公式出現在程式裡，請 Fields 講解

w.attach_grad()
b.attach_grad()
…  …  …
def sgd(params, lr, batch_size): 
    for param in params:
        param[:] = param - lr * param.grad / batch_size

“我們從上上次從數學來談mini-Batch Gradient Descent 演算法，的確是要計算下列的損失函數的對w,b 參數的導數，因為這個幾乎全部有用到梯度下降的演算法都用的到，所以Mxnet 就把這個做成標準作法，只要在參數下 .attach_grad()，後續它將幫忙自動計算梯度（導數），這個並不神奇，例如 PyTorch 也可以用 這樣的語法 torch.ones(2, 2, requires_grad=True) 來讓參數可以自動計算梯度。

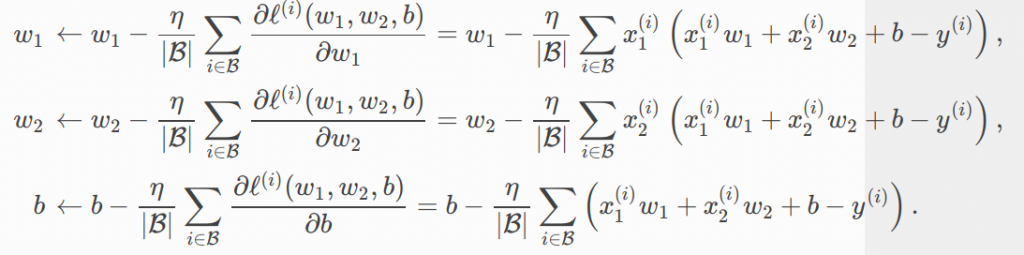
net = linreg
loss = squared_loss

for epoch in range(num_epochs): 
    for X, y in data_iter(batch_size, features, labels):
        with autograd.record():
            l = loss(net(X, w, b), y)  # l 是mini-Batch 裡所有樣本 X 及 y 的損失計算用 
        l.backward()  #用損失函數 loss=squared_loss 反向傳播計算梯度
        sgd([w, b], lr, batch_size)  # 利用梯度與學習率來更新參數
    train_l = loss(net(features, w, b), labels)

所以從上面兩段的程式碼來看，自動梯度計算必須有損失函數或目標函數的定義，然後還需要依梯度與學習率來更新所有的參數後，再迭代反覆的優化讓損失函數最終到平穩不再降低為止。

備註：

專案緣起記錄在 【UP, Scrum 與 AI專案】