在Fields一口氣講完 Linear Regression 以機器學習來計算最佳解，馬上有一些問題，首先佳麗不解的是：

”為何只有兩個特徵，面積與屋齡？而且還房價還只能與特徵有線性關係，難道不能開根號之類的關係嗎？”

Pete 立即搶答：”因為這是練習啦！幾個變數都可以，用兩個變數是因為可以少打幾個字，而且比較容易用視覺圖示呈現損失函數與特徵值的關係。我還有看過只用一個變量來說明的。”

Fields 補充：“線性迴歸模型的確不見得可以做好房價的預測，事實上因為他只有單層網路，無法解釋真實世界的問題，後面我們會再深入一點，做所謂的多層感知機 Multi-Layer Perceptron，MLP。多層的神經網路，或者說深度神經網路，較複雜的模型就更能貼近現實問題，特徵與目標值之間就不會只是線性關係。如 Pete 所言，因為是練習，目的讓大家知道機器學習有三大條件：數據，損失函數，還有演算法。”

Molly 聽到損失函數，提醒 Fields 解釋一下為何要採用MSE，Mean Squared Error

Fields 說明：”損失函數也有人稱為目標函數，雖然學理上只要能將預測值與正確值的誤差表達出來，誤差越大損失值就必須跟著大，就可以。但是因為不同的函數對求導數，梯度計算的複雜度還有是否對演算法的收斂有加速等是有關係的，所以我們會因為不同的問題採用不同的損失函數。舉例來說，如果是分類問題，MSE 就派不上用場，一般會採用 Cross Entropy。這在後面的 Logistic Regression 的問題會說明。採用哪種損失函數這問題，不光是靠數學分析就可以得到答案，它跟資料數據也有關，例如：同樣是線性迴歸問題，一般的數據採 MSE有不錯的效果；但是如果資料有很多的異常值，採用Mean Absolute Error，MAE可能反而比較好。我建議我們先沿用別人的作法，再看有無改良空間。”

討論告一段落，又開始進入實作，Fields 因為採用 mxnet 作為框架，語法比Tensorflow簡單一點點，佳麗也可以猜出每段程式碼的用意，以下取材自 动手学深度学习

%matplotlib inline
import random #用隨機值 製造出虛擬的房價與(面積，屋齡)數據
from matplotlib import pyplot as plt #為了畫圖呈現數據
from IPython import display   
from mxnet import autograd, nd #利用 mxnet 計算梯度，ndarray 置放數據

正常情況訓練數據應該是收集來的，這邊我們隨機製造1000筆，這一千筆資料房價關係，我們假設如下：

成交價格為 ＝ 25 萬元 x （面積）— 6萬元 x （屋齡）+ 80萬元（屋價的起始值，上一篇文所提到Bias偏差 ）+ (個案因為屋況價差產生的浮動值)。

為了表達兩個特徵 以及 我們用 X 來代替；同樣的我們以 w 來代替兩個權重 以及 ，前篇文的房價公式：

房價這個Label y變成就可以用更簡潔的線性代數符號來表達，這又可對應到 mxnet 的 ndarray:

按照上面提到房價公式，這樣我們就可以 [25,-6] 來紀錄 w；80 來紀錄 b

num_features = 2 #有兩個特徵 x1（面積）；x2（屋齡）
num_examples = 1000 #我們製造1000筆的虛擬房價樣本
true_w = [25, -6] #單位『萬元』,每坪25萬元，每年折價6萬
true_b = 80 #屋價的起始值 80 萬元
features = nd.random.normal(loc=30, scale=6, shape=(num_examples, num_features))
#面積與屋齡兩者我們都簡單的用平均面積30坪（年），標準差6坪（年）的標準分配來取值，反正是虛構的
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b #房價Label

但是真實房價總有屋況的差異，我們用 來代表屋況價差，所以虛擬的房價數據Label產生公式變成：
+

屋況價差 我們用平均為0，標準差2萬元的標準分配來取得。

labels += nd.random.normal(scale=2, shape=labels.shape) #房價Label再加上屋況價差
print(features[0], labels[0]) #印出我們虛構的第一筆房價與(面積，屋齡)數據

我們會看到
[33.177837 23.333397]
<NDArray 2 @cpu(0)>
[769.41327]
<NDArray 1 @cpu(0)>
類似的數值。33.178坪，23.333年的房子，賣了 769.413萬元，看來不像是台北的房子，也許在新竹吧。

def use_svg_display(): #用向量圖來看所有數據
    display.set_matplotlib_formats('svg')

def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    plt.rcParams['figure.figsize'] = figsize 

set_figsize()
plt.scatter(features[:, 0].asnumpy(), labels.asnumpy(), 1); #只畫出面積與屋價的關係

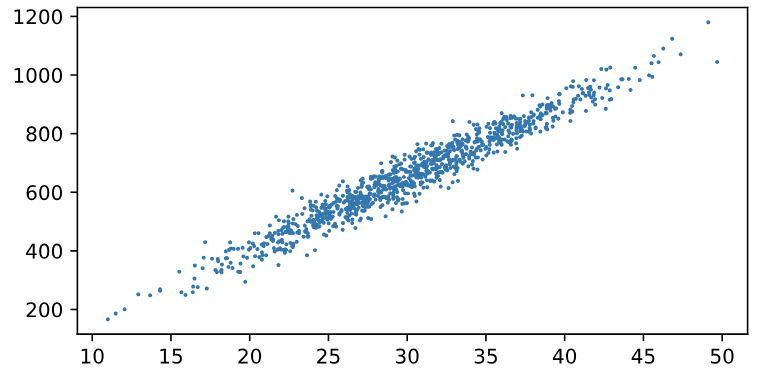
這樣的圖，我們看到了面積與屋價的線性關係

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)  
    for i in range(0, num_examples, batch_size):
        j = nd.array(indices[i: min(i + batch_size, num_examples)])        
        yield features.take(j), labels.take(j) 

這個函數是用來批量的抓上一篇文 mini-Batch 數據用的，我們另外一篇文章特別講他
我們要開始進行上一篇文演算法的幾個步驟

1.先隨機給予w,b參數

w = nd.random.normal(scale=.1, shape=(num_features, 1))
b = nd.zeros(shape=(1,))

#給予梯度計算，這是 mxnet 提供幫助計算梯度的工具
w.attach_grad()
b.attach_grad()

#定義線性迴歸
def linreg(X, w, b): 
    return nd.dot(X, w) + b 
    
#MSE損失函數    
def squared_loss(y_hat, y): 
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

#定義 mini-Batch stochastic gradient descent    
def sgd(params, lr, batch_size):
    for param in params:
        param[:] = param - lr * param.grad / batch_size

2.開始訓練模型

batch_size = 10 #設 miniBatch 每次以10筆
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):  
    for X, y in data_iter(batch_size, features, labels):
        with autograd.record():            
            l = loss(net(X, w, b), y)          
        l.backward()          
        sgd([w, b], lr, batch_size)  
        l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch+1, l.mean().asnumpy()))

這樣我們就完成訓練

print(w,b)

Fields 留一手要大家自己實際跑一下，如果沒有意外，數字應該很接近 [25, -6], 80，亦即經過拿1000筆的數據訓練後，模型也找到了每坪25萬，每年折價6萬，起始價格是80萬起跳。