先說說什麼是分群?分群就是對所有數據進行分組,將相似的數據歸類為一起,每一筆數據的能有一個分組,每一組稱作為群集 (Cluster)。那分類根據什麼來定義,常用距離來做運算。
K-means 分群 (K-means Clustering),其實就有點像是以前學數學時,找重心的概念。
概念是這樣的:
反覆 2、3 動作,直到群集不變,群集中心不動為止。
而k-means分群的時間複雜度為 O(NKT) , N 是數據數量, K 是群集數量, T 是重複次數。我們無法預先得知群集數量、重複次數。數據分布情況、群集中心的初始位置,都會影響重複次數,運氣成份很大。
(黃色是群集中心的初始點,綠色為新的群集中心。)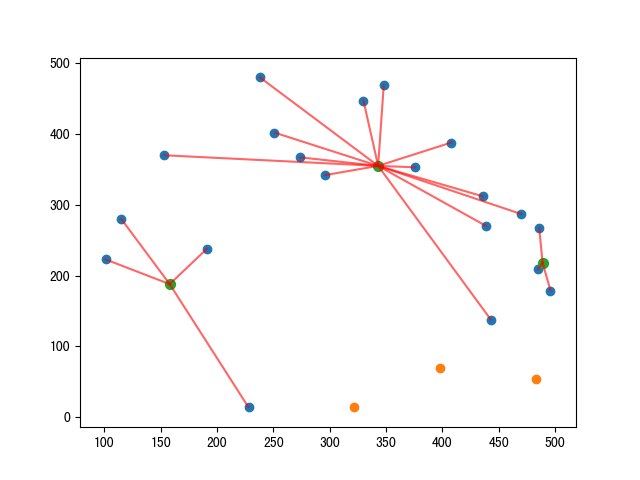
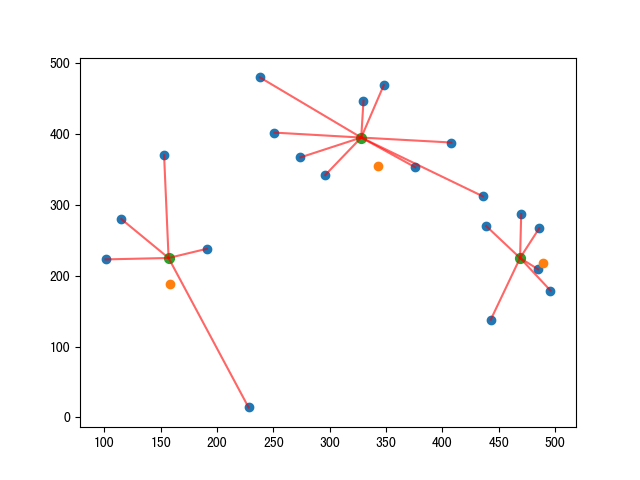
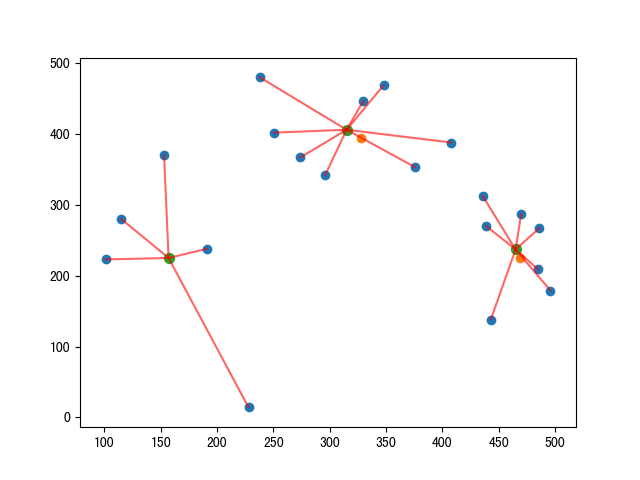
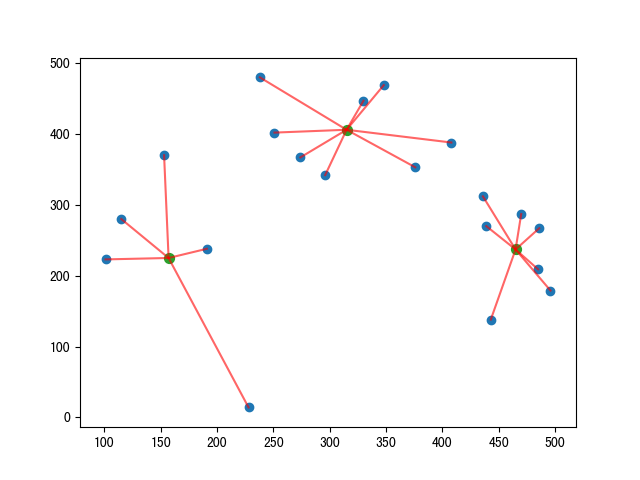
新的群集中心會不斷的更新,直到不動為止。
import numpy as np
import matplotlib.pyplot as plt
# 群集中心和元素的數量
seed_num = 3
dot_num = 20
# 初始元素
x = np.random.randint(0, 500, dot_num)
y = np.random.randint(0, 500, dot_num)
# 初始群集中心
kx = np.random.randint(0, 500, seed_num)
ky = np.random.randint(0, 500, seed_num)
# 兩點之間的距離
def dis(x, y, kx, ky):
return int(((kx-x)**2 + (ky-y)**2)**0.5)
# 對每筆元素進行分群
def cluster(x, y, kx, ky):
team = []
for i in range(3):
team.append([])
mid_dis = 99999999
for i in range(dot_num):
for j in range(seed_num):
distant = dis(x[i], y[i], kx[j], ky[j])
if distant < mid_dis:
mid_dis = distant
flag = j
team[flag].append([x[i], y[i]])
mid_dis = 99999999
return team
# 對分群完的元素找出新的群集中心
def re_seed(team, kx, ky):
sumx = 0
sumy = 0
new_seed = []
for index, nodes in enumerate(team):
if nodes == []:
new_seed.append([kx[index], ky[index]])
for node in nodes:
sumx += node[0]
sumy += node[1]
new_seed.append([int(sumx/len(nodes)), int(sumy/len(nodes))])
sumx = 0
sumy = 0
nkx = []
nky = []
for i in new_seed:
nkx.append(i[0])
nky.append(i[1])
return nkx, nky
# k-means 分群
def kmeans(x, y, kx, ky, fig):
team = cluster(x, y, kx, ky)
nkx, nky = re_seed(team, kx, ky)
# plot: nodes connect to seeds
cx = []
cy = []
line = plt.gca()
for index, nodes in enumerate(team):
for node in nodes:
cx.append([node[0], nkx[index]])
cy.append([node[1], nky[index]])
for i in range(len(cx)):
line.plot(cx[i], cy[i], color='r', alpha=0.6)
cx = []
cy = []
# 繪圖
feature = plt.scatter(x, y)
k_feature = plt.scatter(kx, ky)
nk_feaure = plt.scatter(np.array(nkx), np.array(nky), s=50)
plt.savefig('/yourPATH/kmeans_%s.png' % fig)
plt.show()
# 判斷群集中心是否不再更動
if nkx == list(kx) and nky == (ky):
return
else:
fig += 1
kmeans(x, y, nkx, nky, fig)
kmeans(x, y, kx, ky, fig=0)
