目標:
這題主要目的在於延伸前面解過的題目,
再進行一點變化,同樣屬於DP的範疇。
原題:
Question:
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).
Now consider if some obstacles are added to the grids. How many unique paths would there be?
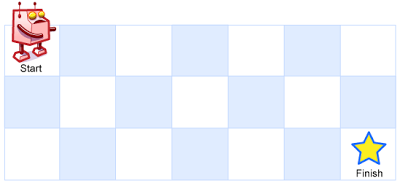
An obstacle and empty space is marked as 1 and 0 respectively in the grid.
Note: m and n will be at most 100.
Example 1:
Input:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
分析/解題:
這題基本上就是前面Unique Paths I的續集,在棋盤上存在障礙物。
如果我們考慮某個點是障礙物的話,其造成的影響會是什麼呢?
建議讀者可以自行畫幾條路徑試試看,這個狀況下,
會造成的結果為:
我們最開始先檢查輸入的方格是否正常,且第一個如果被擋的話,
代表完全走不出去,直接回傳0即可。扣除掉這個狀況的話,
接著從原點開始的方法數就是1。接下來便可由此開始進行dp。
先定義好儲存path的二維陣列並將1放到原點,
依序對每個方格檢查,只要確定它不是障礙物,
就依照判斷將該加上去的部分加上去。
(加到左邊或上面是障礙物的點沒關係,因為它已經是0了)
全部遍歷過一次以後,回傳右下角的值即可。
Java:
class Solution {
public int uniquePathsWithObstacles(int[][] obs) {
if (obs == null || obs[0][0] == 1) return 0;
int m = obs.length;
int n = obs[0].length;
int[][] res = new int[m][n];
res[0][0] = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (obs[i][j] != 1) {
if (i - 1 >= 0) res[i][j] += res[i - 1][j];
if (j - 1 >= 0) res[i][j] += res[i][j - 1];
}
}
}
return res[m - 1][n - 1];
}
}
Python的部分要特別留意二維列表的生成,
請勿使用[[0] * n] * m,這樣在第二層會產生m個指向相同位址的列表。
(第一層不會,因為0的部分還是基本型態而非物件)
(也就是動其中一個row會同步改到其他的row)
我們可以使用二層的List Comprehension來處理,或者第一層用 * ,
第二層用List Comprehension亦可,這裡示範後者。
(實測上兩者速度並無明顯差異)
Python:
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
if not obstacleGrid or obstacleGrid[0][0] == 1: return 0
m, n = len(obstacleGrid), len(obstacleGrid[0])
res = [[0]*n for _ in range(m)]
res[0][0] = 1
for i in range(m):
for j in range(n):
if obstacleGrid[i][j] != 1:
if i-1 >= 0:
res[i][j] += res[i-1][j]
if j-1 >= 0:
res[i][j] += res[i][j-1]
return res[-1][-1]
面試實際可能會遇到的問題:
「時間/空間複雜度?」
(O(mn), O(mn),因我們會遍歷整個二維列表,
且需要另一個二維列表來儲存中間的方法數)
從LeetCode學演算法,我們下次見囉,掰~
下篇預告:
0283. Move Zeroes (Easy)
