這一篇主要是以機率來解釋classification，以下是以李宏毅老師機器學習的課程為主要說明，以下是以神奇寶貝為例子。
由下面這張圖，假設要做一個binary classification，必須找到一個function g，當input x滿足g(x) > 0時，我們就說他是class1；反之，如果input x滿足g(x) < 0時，我們就說他是class2。如果實際與模型判斷出來class不一樣的資料數量越多，代表loss越大，以下有提供幾種方法來降低loss function，這之後會提到，目前將以機率的方式來解決。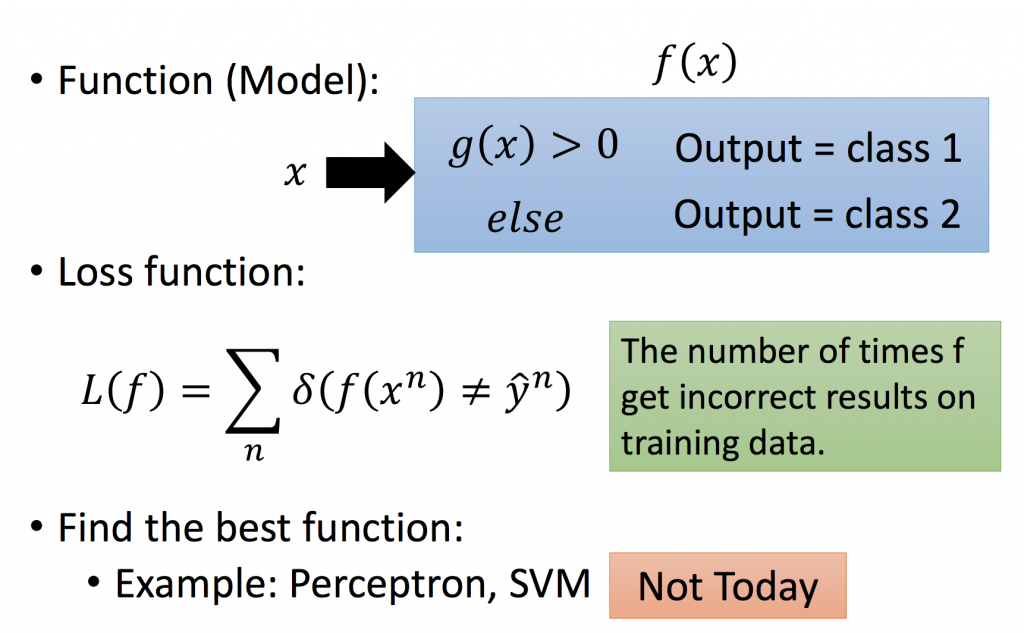

Two class
由下面的圖可得知，要求出x屬於class1的機率為下面式子所示，所以希望從training data估測出P(C1), P(x|C1), P(C2), P(x|C2)，得到這四個機率後，就可以求出Generative Model P(x)，某個x出現的機率。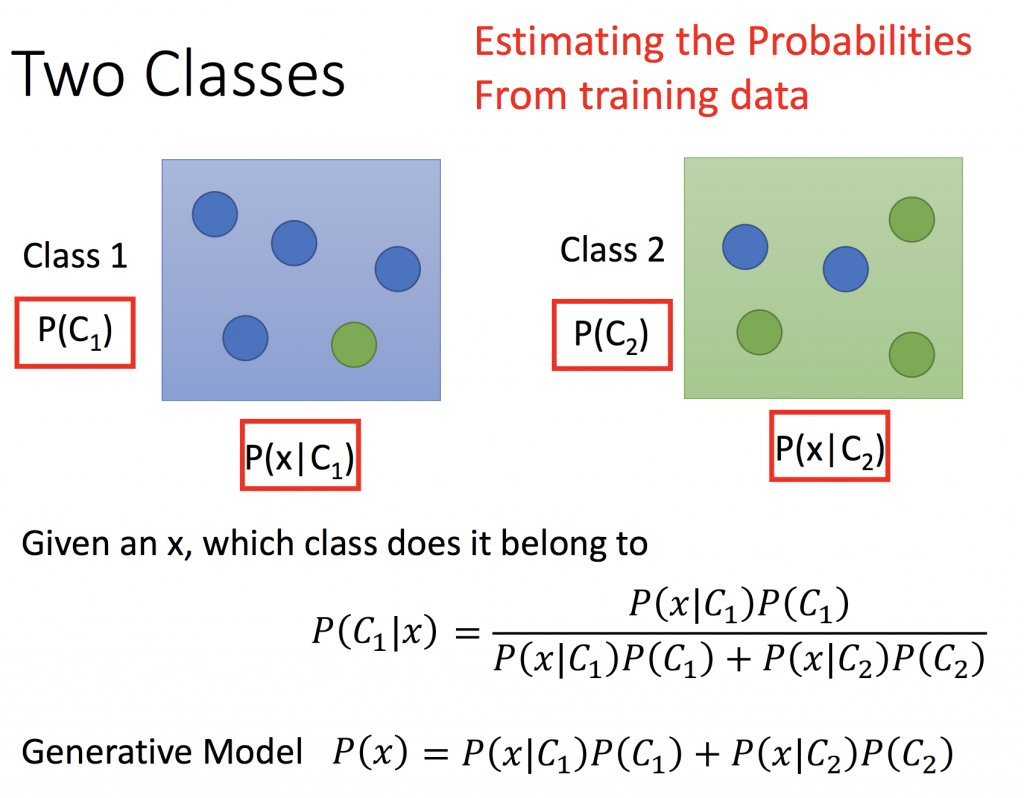

class1（水系）有79筆資料，class2（一般系）有61筆資料，我們可以知道P(C1)與P(C2)的機率分別為多少。

從下面這張圖可以看到，從神奇寶貝的兩個特徵分別是Defense及SP Defense，可以得知從水系神奇寶貝中挑選該神奇寶貝的機率是多少，如何從已知的神奇寶貝資料中估測新的神奇寶貝出現機率？

這79隻神奇寶貝是從Gaussian Distribution產生出來的，也就是說從所有水系神奇寶貝sample出來的，所以要知道新的神奇寶貝的機率也必須透過這個Gaussian Distribution來求出。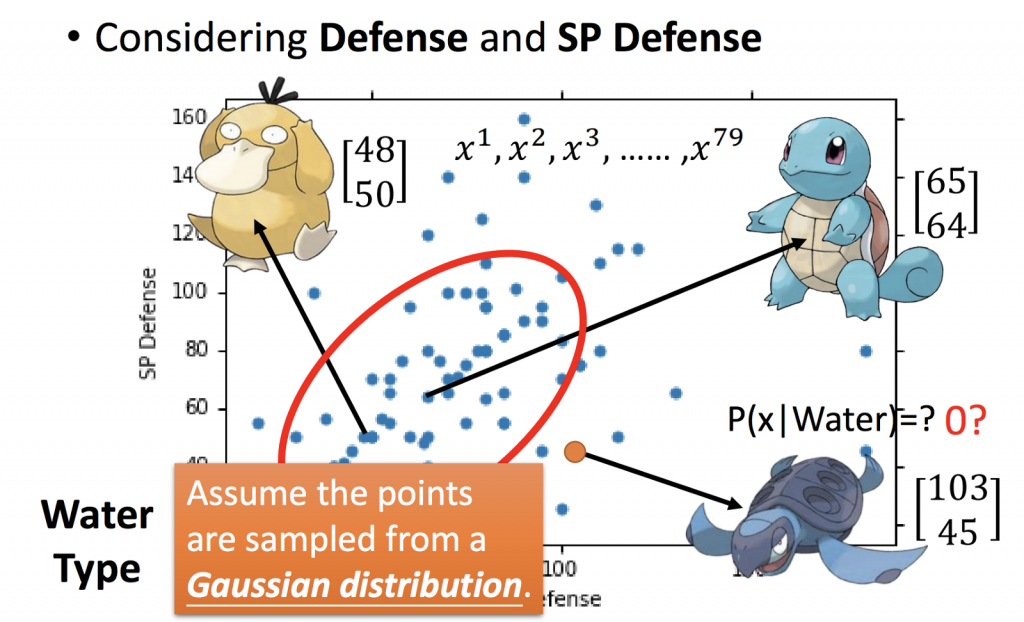

Gaussian Distribution:
首先，要從這79比資料，求出這個Gaussian Distribution:

可以把input x看成是一隻神奇寶貝的數值，output就是這隻神奇寶貝的機率。不同的mean及covariance matrix所產生的分部也不一樣。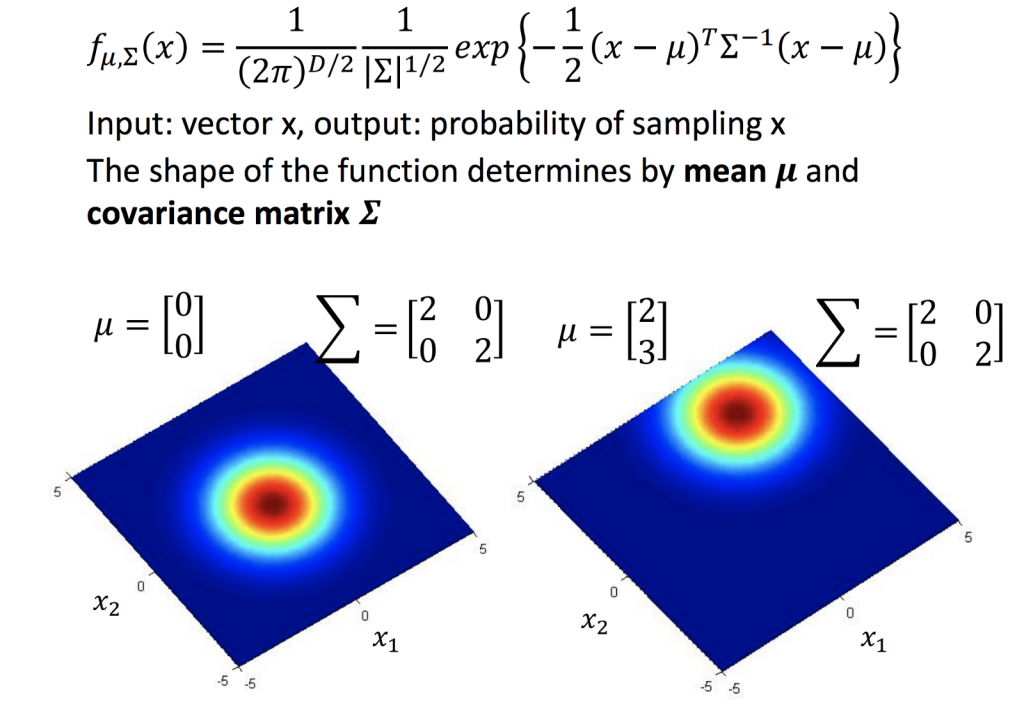


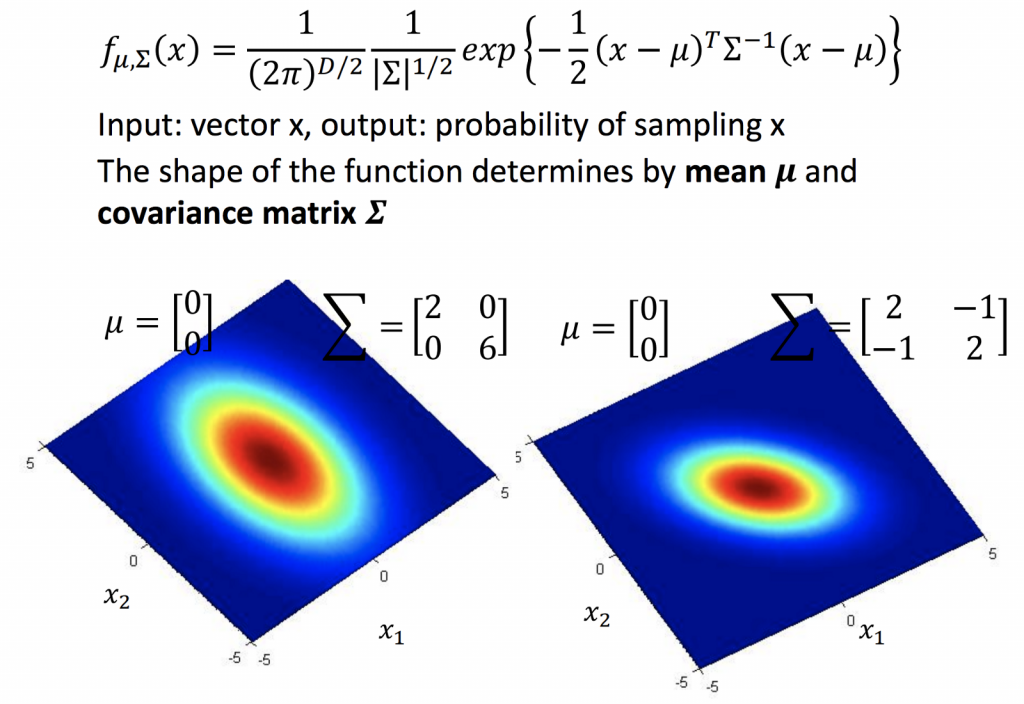
如果能從已知的79筆資料，來估測此Gaussian Distribution的 mean及covariance matrix，我們就可以寫出下面的式子，透過這個式子，得知一隻新的神奇寶貝在這個Gaussian Distribution所sample出來的機率。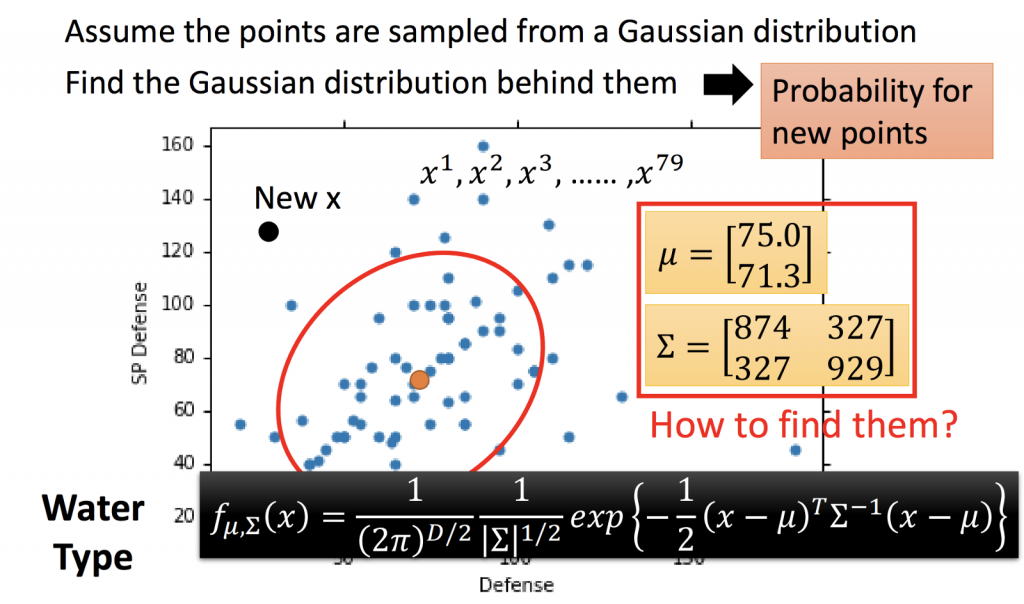

Maximum Likelihood:
由下圖可以看到，任何一個mean及covariance matrix所產生的Gaussian Distribution都能產生一些資料的點，例如左下角那一組mean及covariance matrix所sample出左下角點的機會比較大（因為點離圈圈較近），右上角那一組mean及covariance matrix所sample出左下角點的機會比較小（因為離圈圈較遠），也就是說左下角的Gaussian Distribution所能sample出這79個點的機率比較大；反之，右上角的Gaussian Distribution所能sample出這79個點的機率比較小。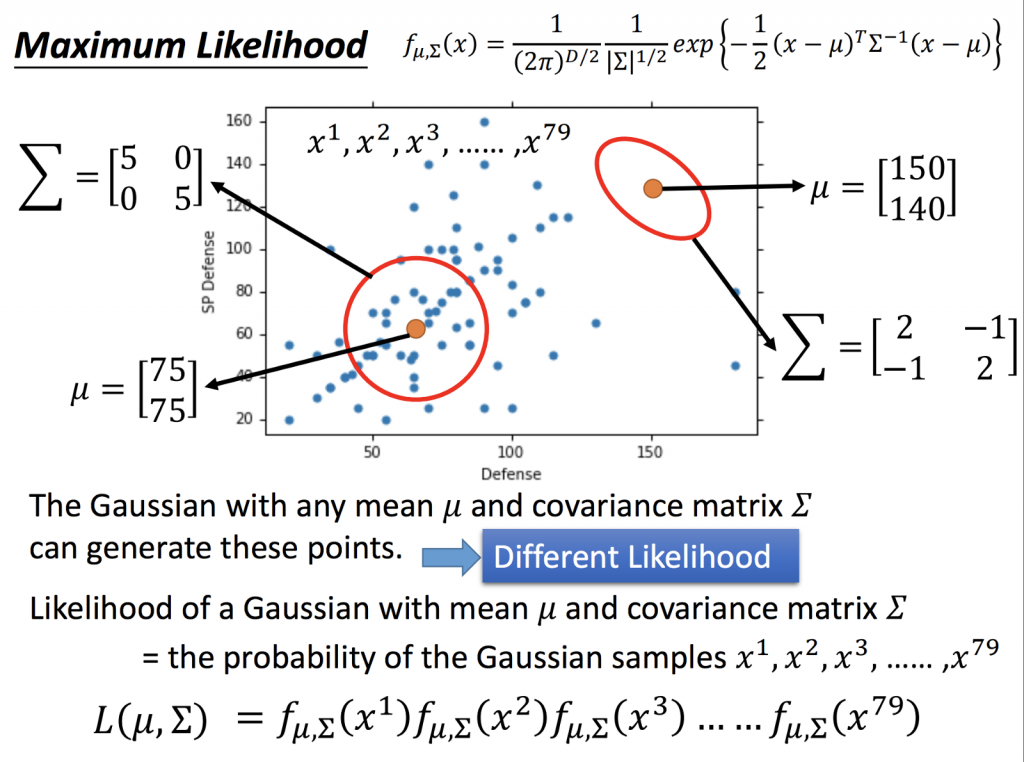

所以我們要找一個Gaussian Distribution，使得sample出這79個點的機率為最大，也就是說我們要找出Maximum Likelihood。根據前面所提到的mean及covariance matrix，所以我們要找到一組mean及covariance matrix 使得Likelihood最大。

當我們求出mean及covariance matrix後，就可以來做分類了，下面的圖可以看到，以0.5當作門檻值，當P(C1|x) > 0.5，我們可以說這隻神奇寶貝是屬於水系神奇寶貝。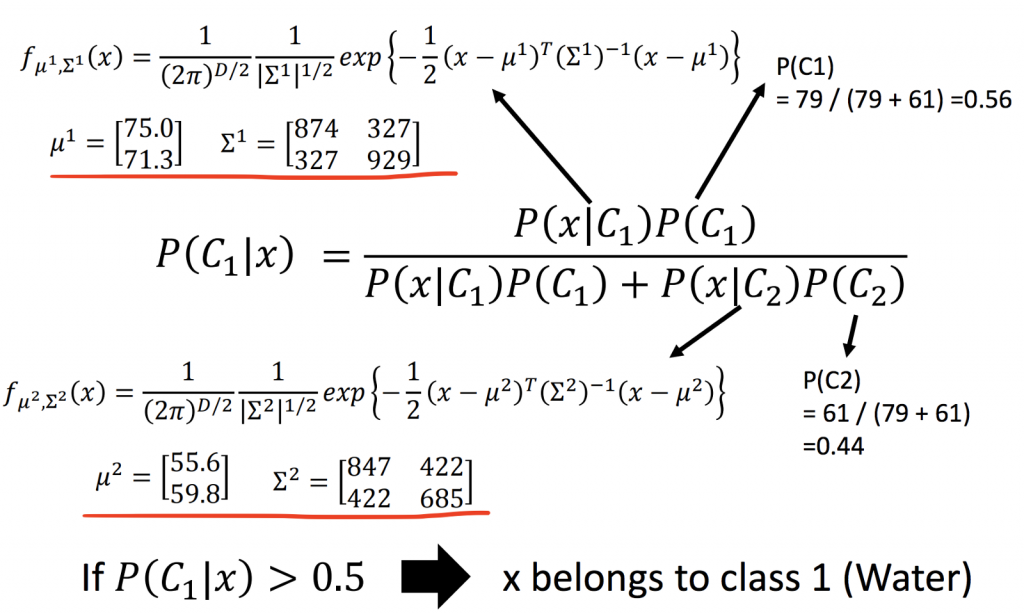

modify model:
上面有提到，每一個Gaussian Distribution都有相對應的一組mean及covariance matrix。由下面的圖可以知道，我們目前只考慮兩個變數，分別為Defense及SP Defense，所以covariance matrix為一個二維陣列，也就是說covariance matrix跟input的feature size的平方成正比，如果covariance matrix的數量越多，變數就越多，也越容易造成overfitting。
所以為了解決這個問題，常見的作法為，share相同的covariance matrix給這兩個分類的Gaussian Distribution。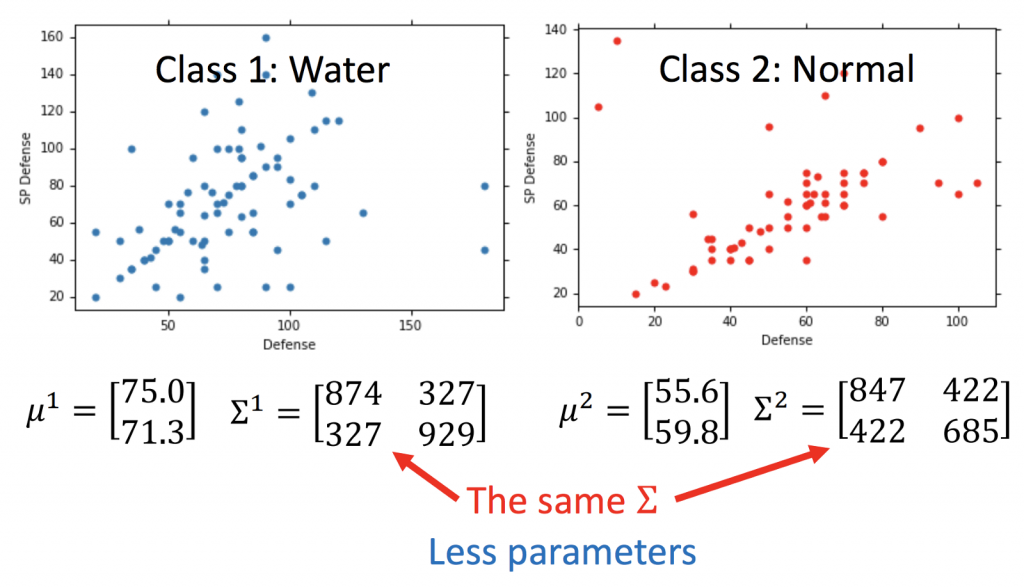


所以可以發現使用相同的covariance matrix，可以更明顯的分類。

Warning of Math

經過一連串的推導可以得到下面的式子（詳細推導過程可以參考李宏毅老師的影片https://www.youtube.com/watch?v=fZAZUYEeIMg），
這也就是為什麼在分類中boundary會成線性。