在上一篇文中，我們介紹了ML問題的兩個主要分類。現在讓我們更詳細的來深入學習這兩者的差別吧!

回歸與分類

　　回到上篇文章的餐廳例子，我們想要利用客人帳單的總額來預測客人會給的小費數量。小費的金額是連續的，所以這問題基本上是回歸問題。

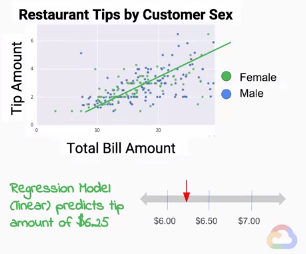
在回歸問題中，我們會建立數學模型來預測標籤的連續值。假設我們得出小費金額會是帳單總額的18%，則斜率便是0.18。目前為止是國中程度的內容，相信大家都能理解。我們在這單個特徵二維的線性問題的模型，事實上也能推廣到擁有多的特徵的多維問題中。我們將每個例子每個特徵的每個值乘以超平面(hyperplane)的梯度，便能將一條線泛化得到標籤的連續值。

關於超平面的基本概念可以參考這裡，數學推導可以參考這裡。

在回歸問題中，我們希望能夠最小化預測的連續值以及標籤的連續值之間的誤差(bias)。在這邊我們常使用均方誤差(MSE)。

針對均方誤差可能需要介紹損失函數，但礙於篇幅限制本文並不會介紹。有興趣且有一定統計學基礎的讀者可以參考這裡。

　　在上篇文章的第二個問題當中，我們試圖預測性別－也就是二分類問題，並且使用帳單總額與小費數目來預測。事實上若我們真的如此做，你可以預見這會是一個表現不怎麼好的模型，因為透過觀察，男性和女性在圖上並沒有明顯的分布傾向差異。

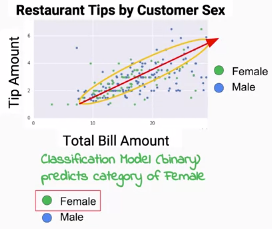
在分類問題之中，我們必續製造出一個決策邊界(decision boundary)來區分不同的類別，而非預測連續變量。我們可以發現在上圖中，簡單的線性模型並無法解決我們的問題(見圖上紅線)。而決策邊界可能會演變成更多維的超平面(如圖中的黃圈)，我們可能可以假設女性比較集中在黃圈內，男性比較容易分布在黃圈外。而我們要如何評估這兩種決策邊界的優劣呢?在分類問題裡，我們常使用交叉熵(Cross-entropy)。

關於交叉熵，本文也不會額外介紹，必須先理解信息量與熵的內涵。詳細也可參考前面的參考資料，有詳盡的介紹。

回歸與分類，難道不能一起嗎?

　　在這邊我們想拋出讓讀者思考的問題是，概念上我們會認為回歸與分類是互斥的。但事實上，在前面小費的例子中，我們也能將小費的連續量設成級距，如0~15%一組、15~30%一組、30%以上一組，這樣原本的回歸問題就成了分類問題，不是嗎？事實上，在這系列文的後期，我們也有機會討論到完全相反的過程，也就是分類問題怎樣嵌入到回歸問題中。

若是覺得本文有幫助，歡迎點選Like、星星收藏或是追蹤系列文支持哦！