很多機器學習算法最後都被歸納為求解最佳化問題。在各種最佳化問題裡，梯度下降法是最簡單也最常見的一種，因此在深度學習的訓練中被廣為廣用。

最佳化問題

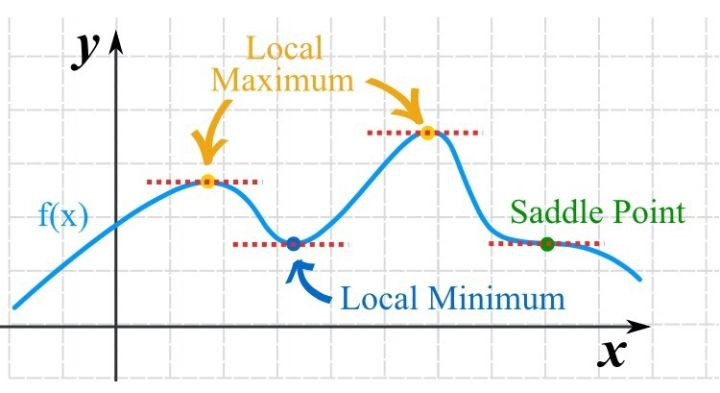
實際應用遇到的問題多半都是多元函數，梯度是導數對多元函數的推廣，它是多元函數對各個自變量偏微分形成的向量。

多元函數的梯度定義為

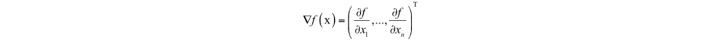
可微函數在某一點存在極值的必要條件是梯度為0，梯度為0的點稱為函數的鞍點，不過梯度為0只是函數取極值的必要非充分條件，也就是梯度為0的點可能不是極值點。

我們可能會想，那麼直接求出函數的梯度函數，然後令梯度為0去解方程式，不就找到最佳化問題的答案了嗎？
理論上是這樣，但是我們會遇到另外一個問題，就是梯度函數可能很難求解。

因此我們只能用另外一個方法，用數值計算的方式求近似解，不斷的疊代，直到所求收斂到極值為止。

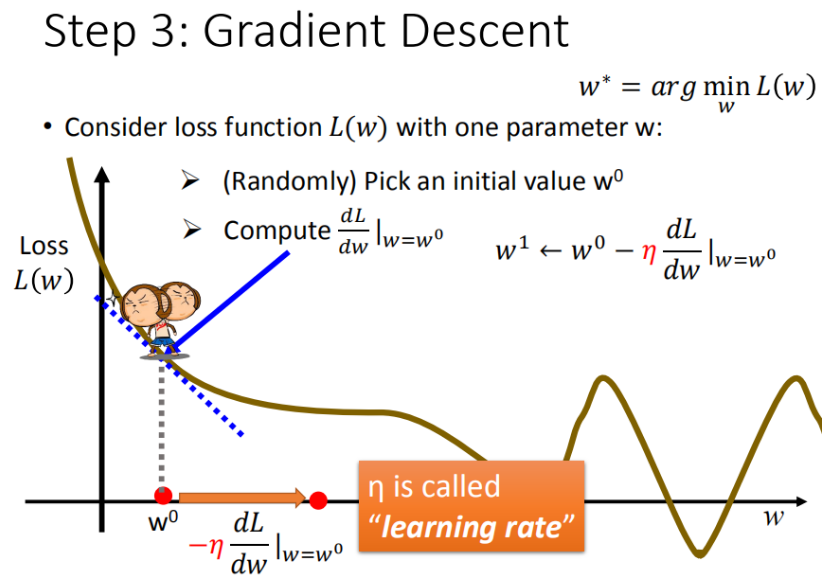
舉個例子來說明數值計算的過程，首先我們假設一個常數 學習率： 移動的步長 η

步驟一：隨機選取一個w^0作為起點
步驟二：計算梯度，根據梯度來作為移動方向的依據，大於0向右走，小於0向左走。
步驟三：每次移動的距離為學習率的大小
重覆步驟2和3，直到抵達極值為止。