在之前的線性迴歸章節中，我們假設目標函數是一元一次方式，也就是一條直線方程。很多時候我們會遇到無法用線性方式擬合數據的情項，這個時候可以將目標函數改成多項式方程。
在多項式迴歸中，我們加入了高次方的特徵項，增加了模型的自由度，因此能更好的擬合數據中的非線性變化。同時我們也增加了模型的複雜度，過擬合的風險也隨之增加。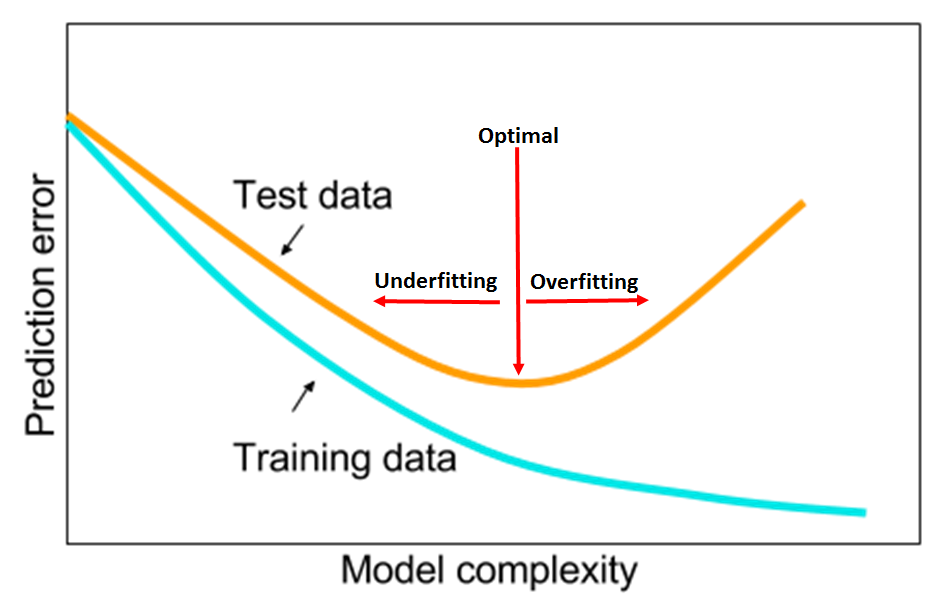
在多項式迴歸中，最重要的參數是多項式裡的最高次方項。我們假設最高次方為n，且只有一個特徵值，此時多項式迴歸方程為：
ℎ̂ =theta * 0+theta 1 * x1+ ... +theta n−1 * xn−1+theta n * xn
令x0=1，在多樣本的情況下，可以改寫成向量化的形式
ℎ̂ =X * theta
iThome鐵人賽
看影片追技術