簡單回顧
在ML_Day5(Linear Regression Introduction)有介紹什麼是Gradient Descent，就是對loss function做偏微分（切線斜率）就是找極大極小值的概念，找一組參數讓loss function越小越好。ML_Day5(Linear Regression Introduction)，我們要更新的是w, b，在這邊用一個theta表示。

Gradient Descent如何運行
這邊可以搭配公式一起看，紅色箭頭就是loss function的gradient方向，當乘上learning rate後再乘上負號（改變方向）就會變成藍色箭頭，一直重複這樣的動作，這就是Gradient Descent的運行模式。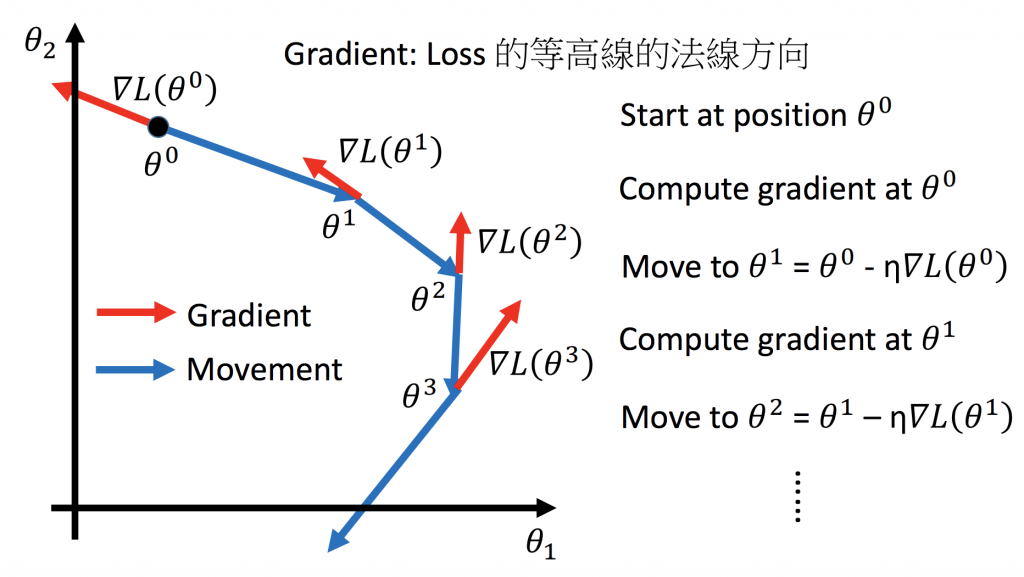

Learning Rate對 Loss Function的影響

• learning rate太小（藍色），永遠到不了最低點。
• learning rate太大（綠色、黃色），錯誤率一直往上飄(overfitting)。
  

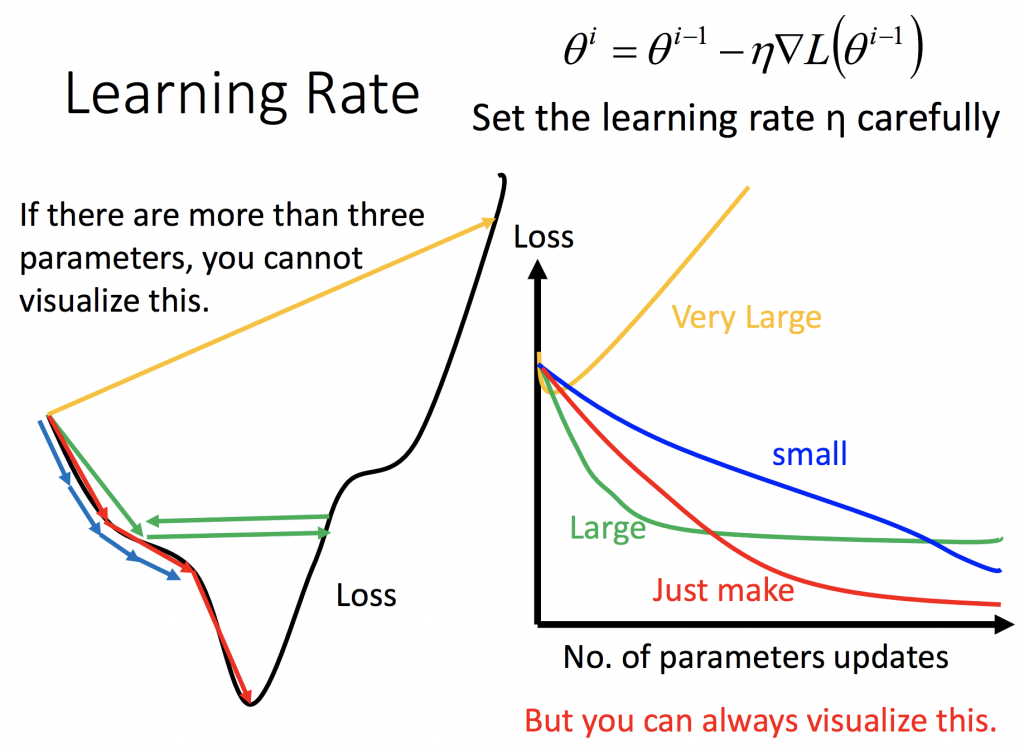
調整learning rate的方法
既然learning rate有時候不是太大不然就是太小，是不是有什麼方法可以來讓機器自己調整。當一開始起始點離最低點還很遠的時候，learning rate可以大一點；當越來越接近最低點時，learning rate要小一點，這樣才能收斂在最低點附近。下面那張圖所示，假設定義learning rate是每次跟著更新次數做調整，也就是說你的更新次數越多，learning rate會跟次數的開根號成反比，learning rate會越小。那有人就覺得說可以根據不同參數調整不同的learning rate，以下會列出幾種方法：

• Adagrad
  現在對於每一個參數w都要給一個不同的?，就是每次更新的?就是等於前一次的?再除以?^t，而 σ^t則代表的是第 t 次以前的所有梯度更新值之平方和開根號(root mean square)，而?只是為了不讓分母為0而加上去的值。
  

• Adagrad反差
  下面圖中的式子可以清楚看出，分子的部分（紅色框框）顯示，當gradient越大，參數update越多；但分母則相反，分母的部分（藍色框框）顯示，當gradient越大，參數update越少。
  
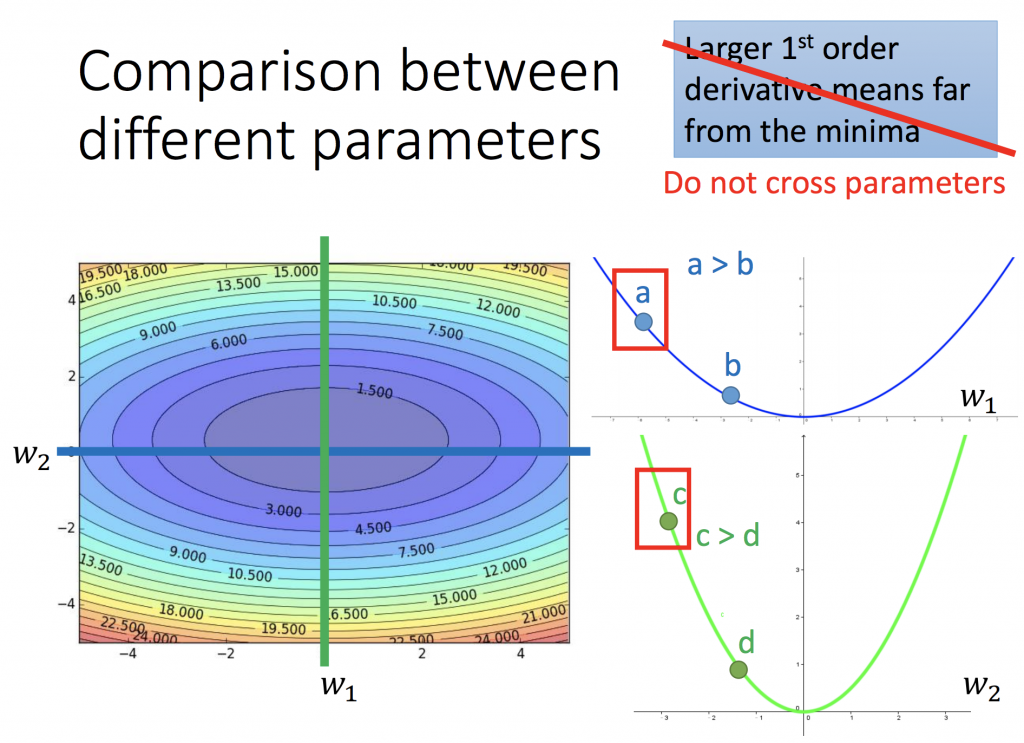
  假設要選一個起始點當作參數更新的最初點，最佳的起始點就如下圖所示的x0（因為只要踏一步就能到最低點，就是對y做一次微分），但這只是在一維函式有用。為什麼我會這樣說呢？如第二張圖所示，比較a, c兩點，a的一次微分 < c 的一次微分，但是a卻是距離最低點是比較遠的。所以為了解決這個問題，必須要除以2a，就是y的二次微分，如此才能在多個參數時，真正比較與最低點的位置。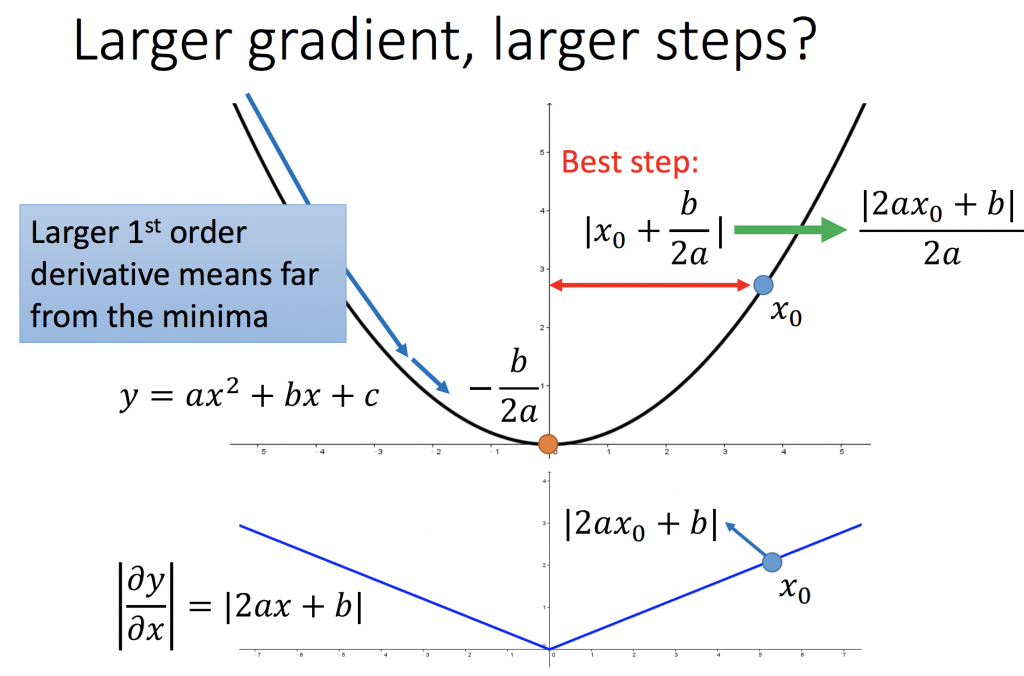
  
  

• 隨機梯度下降法（Stochastic gradient descent，SGD）
  之前有提過，如果要最小化loss function，當要從整個data set計算出梯度後，要朝著下降的方向前進，函數才會收斂。假設有一個data set非常大，那每次在執行梯度下降時，是非常消耗時間的事情，因為要朝著global minimun前進，就需要對整個data計算一次。
  而隨機梯度下降法，可以被視為一種近似梯度下降的方法，通常會更快達到收斂。因為它只需考慮一個example，只對一個example的loss做計算。就像如果也看過棋靈王就會知道，假設今天有20筆資料，用梯度下降法去下圍棋，你必須考慮完這20筆資料才開始下第一步，但如果你用隨機梯度下降法，你已經下了二十步了。