前情提要

昨天發現不同邏輯解法submit後的runtime和memory有不同的結果,今天要來研究下這兩個和"時間複雜度"及"空間複雜度"的關係

進入正題

分享我查到的參考1介紹後理解的內容:
時間複雜度是程式碼執行的時候需要的時間,一般會用O()這個函數計算,念Big-O
簡單敘述,如果函式每次都輸出相同的東西,那他的時間複雜度就是O(1);如果它會隨著輸入n而變動n,時間複雜度就是O(n);函式如果是巢狀迴圈的話,時間複雜度就會變成O(n^幾個迴圈)
空間複雜度則是指程式碼執行的時候需要用到的記憶體空間,同樣也是記成O()
主要是看變數的數量是否會依照輸入而變動,計算的方法和時間複雜度也類似
另外複雜度如果要仔細評估的話,參考2裡說明了複雜度中"最好"、"最壞"、"平均"、"均攤"的計算方式.

我自己查完之後覺得,時間複雜度和演算法設計的方式最有關係,而空間複雜度則和演算法使用的資料結構有關係.
所以昨天用了四種不同的解法: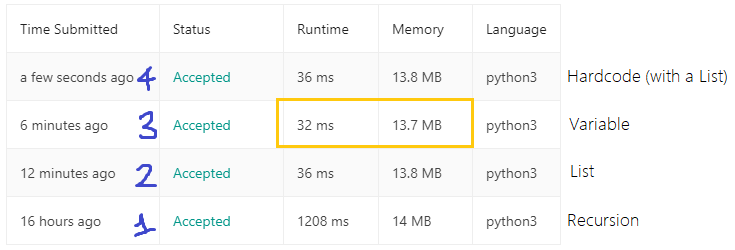

第一種遞迴的方式撰寫,因為每次函式都從最大的往小的呼叫,再一一往外回傳,因此需要最多的時間;改成第二種和第三種作法,都是使用一個for迴圈的,時間就降低成3xms.
另外第二種和第四種做法都是用List的方式,陣列那樣紀錄計算過的資料,需要的空間是一樣的,所以Memory那欄的結果一樣;第三種方式是用變數的方式紀錄,固定就是宣告的那三個變數,所以需要的空間較少;第一種方法則是因為函數呼叫後的回傳值需要空間,計算過程中的變數也需要空間.

不過時間複雜度和空間複雜度計算出來的O()都是理想的狀態,如果是一個程式專案需要計算時間複雜度和空間複雜度的話,每個函式還會因為不同呼叫次數而對整個專案程式整體產生不同的時間複雜度和空間複雜度.

參考資料

參考1資料結構筆記(一)：演算法、時間複雜度、空間複雜度
參考2算法系列-複雜度分析：淺析最好、最壞、平均、均攤時間複雜度