終於進到了我們的重頭戲啦，在上一篇我們介紹到了我們的單層感知機！而我們知道單層感知機其實就類似是一個神經元，它能做簡單的判斷！那麼接下來，我們如果把多個感知機串在一起呢？如果說感知機是一個神經元，那麼串在一起理所當然就是神經網路啦！

Neural Network

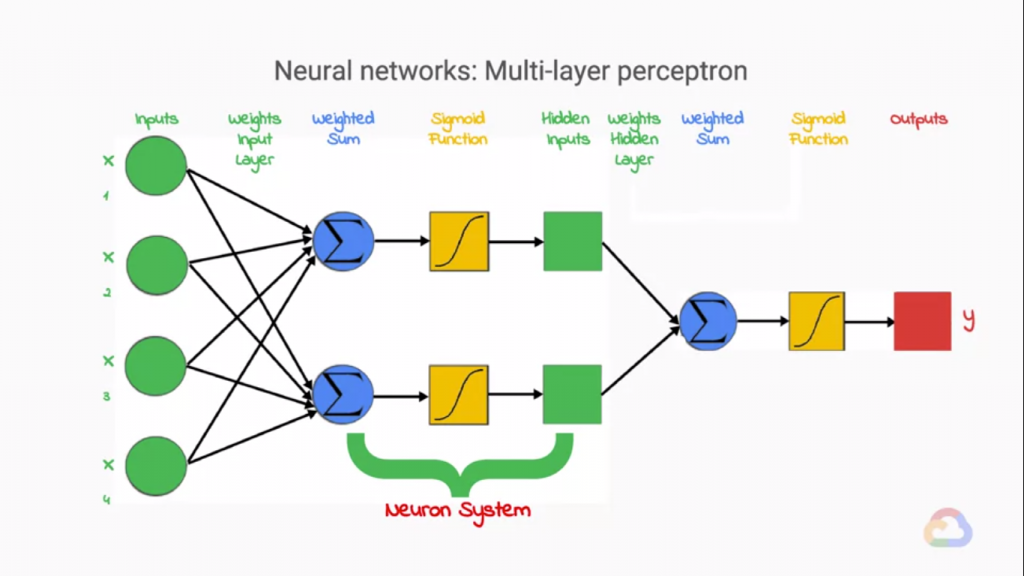
上圖就是神經網路的架構啦，和感知機一樣，我們都必須乘上權重，並計算總合加上偏差，透過非線性的函數輸出值。
為甚麼需要一個非線性的函數來轉換輸出值呢？原因很簡單，當你組合很多個線性的神經元在一起，到最後擬組建的整個神經網路也只會以線性的方式呈現，而在我們要預測的東西總是複雜的，我們沒有辦法透過線性的Function來做預測的，於是我們在每一個神經元後加上一個非線性的函數來"掰彎"我們呈線性的輸出，這時我們發現我們在每一個神經元要輸出時都"掰彎"一下，掰彎了好幾次，我們架構出的神經網路理所當然就不會做線性的預測囉！可以看到上圖的Sigmoid Function 就是非線性函數(或者稱為Activation Function[激活函數])在掰彎神經元輸出值喔。

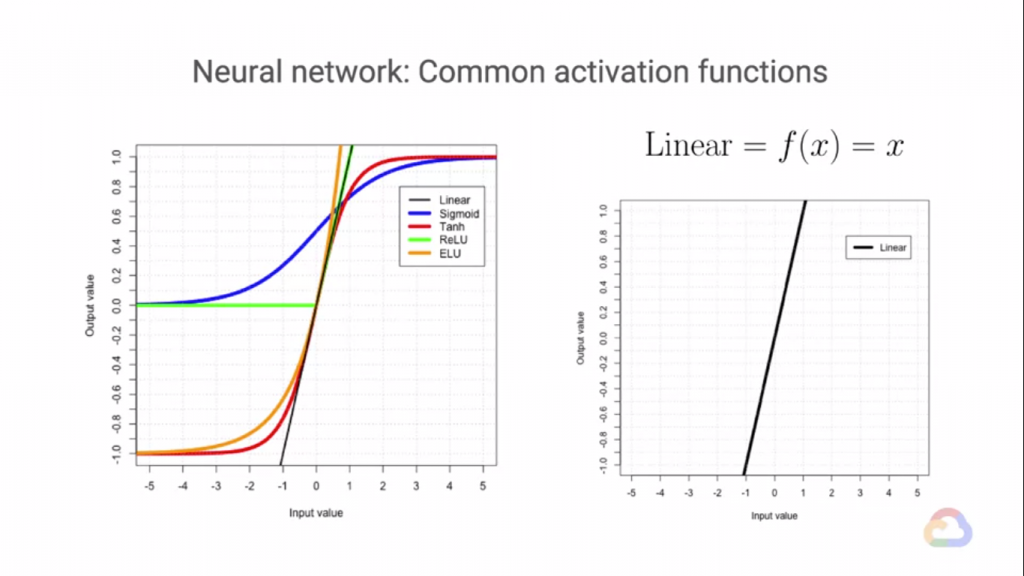
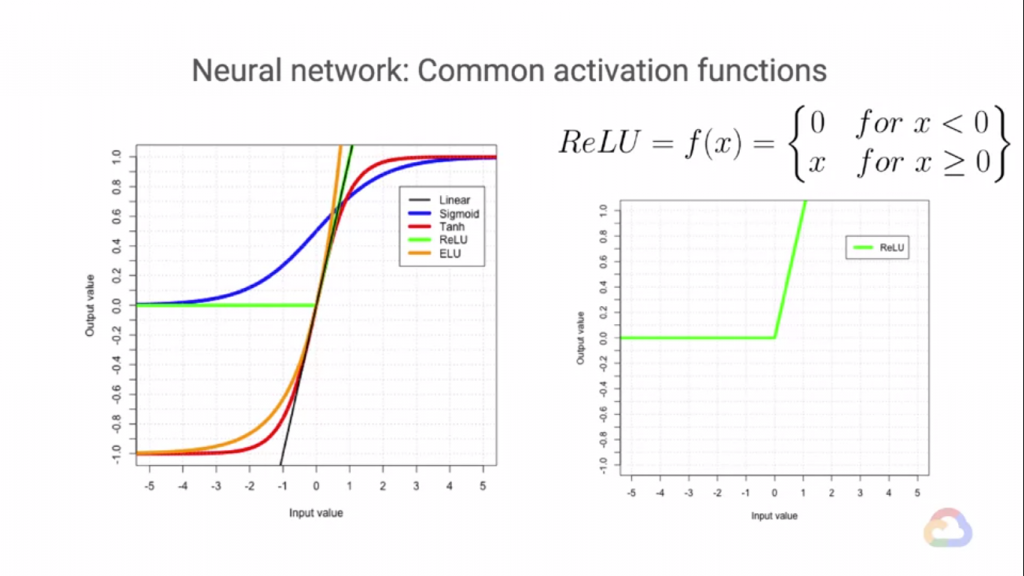
上面是各種非線性的激活函數，在ML的世界裡我們為了要完美的進行預測，常常會捨去模型部分的可解釋性，
而既然我們無法完全知道模型為何可以成功的預測，那麼我們就得多多嘗試，在ML中最重要的就是"經驗"，
而在上面的Ativation Function中，都是我們曾經試過的非線性Function，沒有說哪個Function特別好，
或特別差，不過目前我們最常使用的就是ReLU Function，其他的Function根據以往的經驗會發生一些問題
(Vanish Gradient Problem...等)，不過這不代表ReLU Function就是一個完美無缺的Function，雖然它也會造成一些問題，不過ReLU造成的問題大部分都還在可以接受的範圍內。下圖是ReLU Function。我們當然也可以設計屬於自己模型的Activation Function不過切記，這個函數必須要可以微分，因為我們在做學習時(權重&偏差更新)會將Activation Function微分，如果你的Activation Function不能微分那就代表你的Model是無法學習的！