介紹完神經網路，現在我們要來談Loss Function啦！在神經網路裡，我們有輸入，並會得到神經網路的預測，
不過我們要如何告訴神經網路，它哪裡做錯了？應該要改，這時LossFunction的功用就來了！

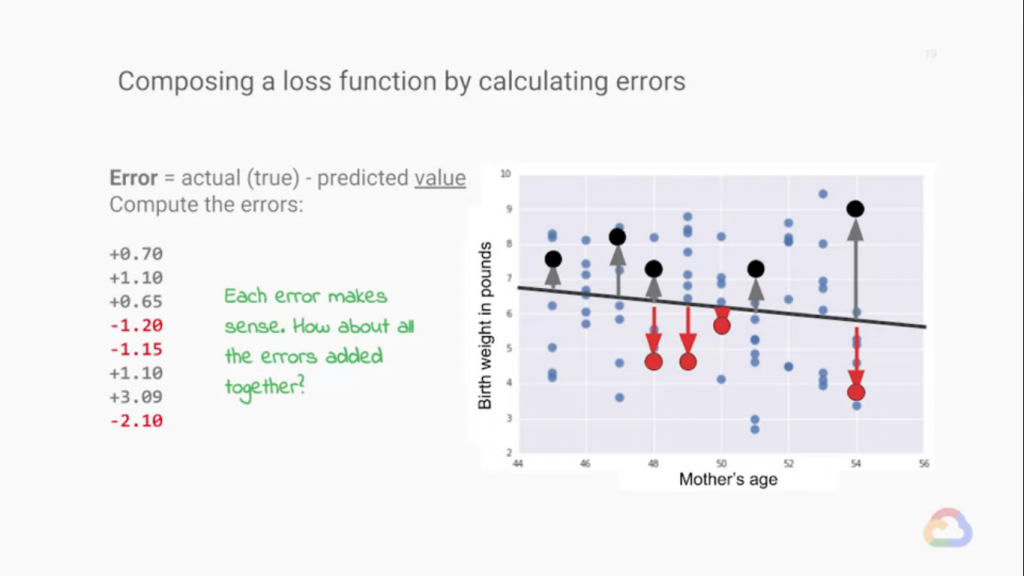
Loss Function

Loss Function是拿來計算神經網路與實際答案的誤差，而計算誤差的方法很簡單，就是實際值減預測值就可以了！
不過這時我們會遇到小小嚴重的問題！那就是當我們把這些誤差加總時，我們的誤差有正有負，而我們通常在訓練網路
時，我們不可能會傳一次資料就進行一次反向傳播更新網路，這樣會使計算變得非常平繁，進行一次Back Prepergation 需要的計算量也很大，我們會把"一群"資料的誤差加總算平均，再進行Back Prepergation，
這樣子的話我們就可以減少Back Prepergation的次數減輕運算量，而回到原本的問題我們的誤差值會正負相消，
造成誤差流失，這該怎麼辦呢？

我們利用MSE來解決這個問題 Mean Square Error ，均方誤差將誤差平方把負值消出。這樣我們加總時就不會被正負
值相消了！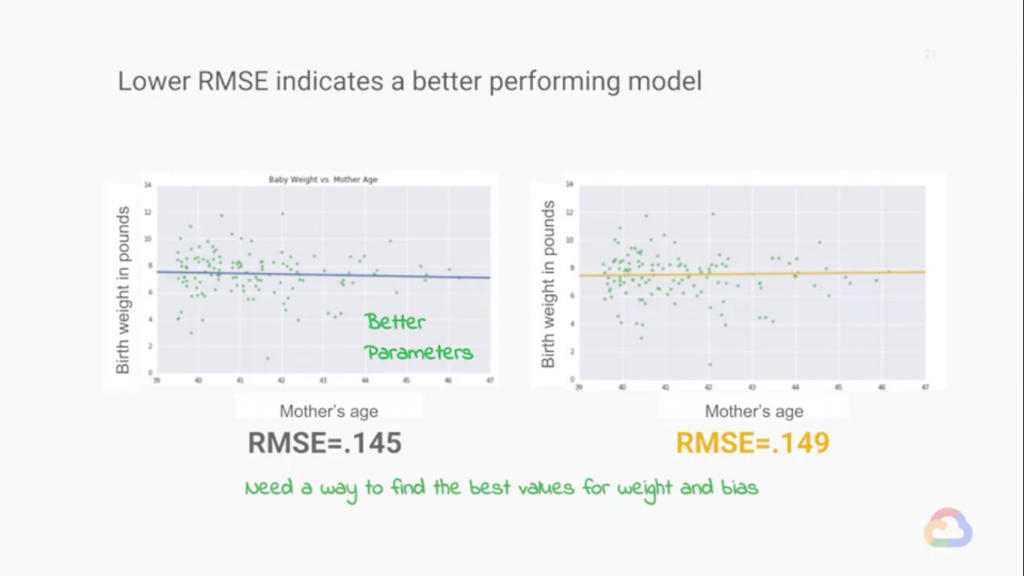

MSE非常適合應用在Regression的問題中，但是在Classification的問題中，用MSE就會出問題了。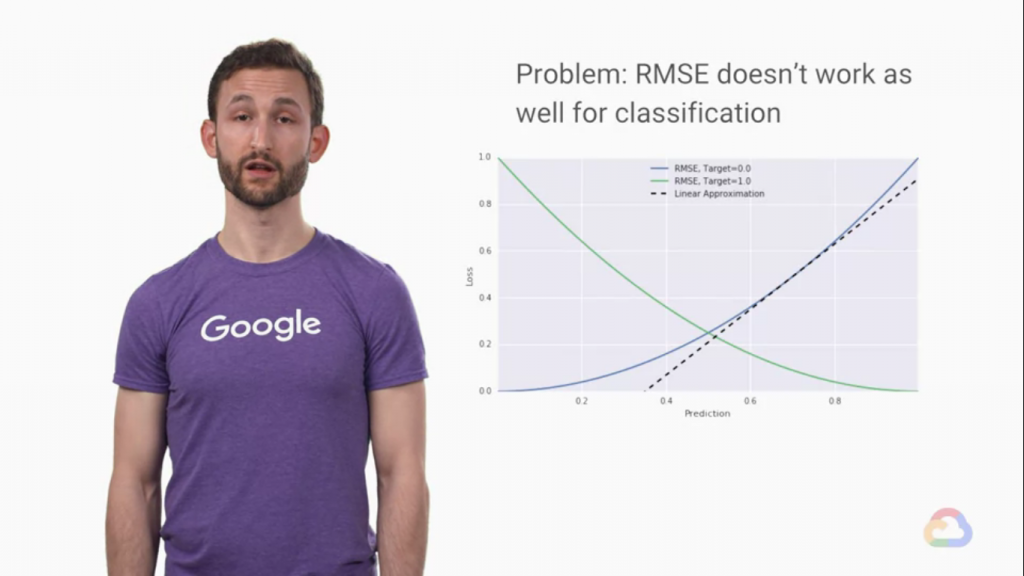

我們前面的文章提到，在回歸問題中，資料的分布越接近網路預測值會越好，不過在分類問題中，我們是想要讓資料離預測線越遠越好，這樣代表模型有更好的包容度！
那麼在Classification的問題中，我們要如何計算誤差呢？

Cross Entropy

交叉熵就是用來計算Classification的問題中的誤差了！

交叉熵的公式歸結為兩個不同的術語。對於給定的數據點，其中只有一個會參與損耗。第一項參與積極的例子，也就是說，例子中的標籤Y是一個。當標籤為零時，第二項參與。在這裡，我們有一張表格，顯示了標籤以及圖像分類任務中兩張圖片的預測。標籤編碼圖片是否描繪了人臉該模型似乎做得不錯。與底部的示例相比，頂部的示例的預測要高得多。讓我們看看該函數是如何工作的。在這裡，損失函數的構造方式，第一個示例的負項和第二個示例的正項都消失了。因此，給定點7和點2的預測，對於帶有標籤1和0的兩個數據點，交叉熵損失有效，第一個數據點的正項，第二個數據點的負項乘以負一半。結果是點13。如果我們的模型沒有做出好的預測，會發生什麼？在這裡，負面示例似乎被錯誤分類，因此損失增加了，這是有道理的，因為請記住，損失是我們要盡量減少的。因此，現在我們知道如何比較參數空間中的兩個點，無論是使用RMSE進行回歸還是使用交叉熵進行分類。[來自課程內容]