在介紹Keras之前，想先分享神經網路，因為keras是一個深度學習的函式庫，而說到深度學習就一定要先提到神經網路。那我們就開始吧～

深度學習

在說明神經網路之前想先概要深度學習的概念，前面的文章有提過深度學習是機器學習的一種技術，這個技術的特點就是神經網路，因深度學習的強大進而使得深度學習被廣泛用於許多場合，如機器視覺、語音辨識等等。而深度學習也有最精簡的三步驟！
Step1：訂定網路架構。
Step2：訂定學習目標。
Step3：開始學！
沒錯沒錯，這是超級濃縮，最難是前面那兩步驟囉！那如果後面能玩到深度學習，會再詳細的介紹並且舉例子。

神經網路(Neural Network)

舉一個簡單的例子

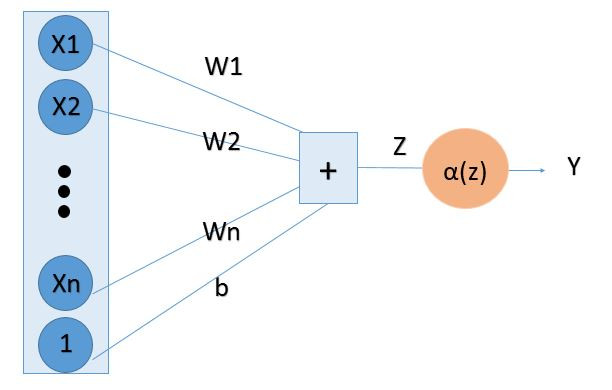
上圖是非常簡單的神經網路架構，顯而易見的可以得到
Z = W1 * X1 + W2 * X2 +　．．．Wn * Xn + b
Y = α(Z)
介紹一下，X是輸入的資料的神經元，一堆神經元又是輸入我們叫做輸入層。那在線上的W那些就是權重，b可以叫做偏差(但也是權重拉~)。α稱作激勵函數，後來會介紹到。最後將加起來的Z經過激勵函數就會是我們的輸出了！

帶數字玩玩看

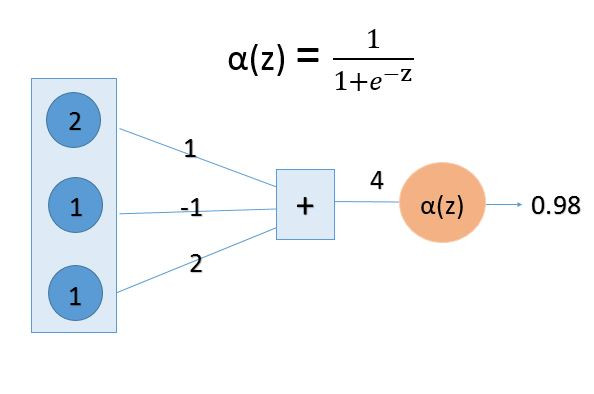
那就從最左邊開始說明拉，1 * 2 + ( -1 ) * 1 + 2 * 1 = 4，到這裡還算簡單，比較酷的就是那個激勵函數！它的公式也附在圖上，將4帶入後就求得輸出0.98拉！
那酷酷的激勵函數會到下面在補充！

真正神經網路複雜長相

圖片出處
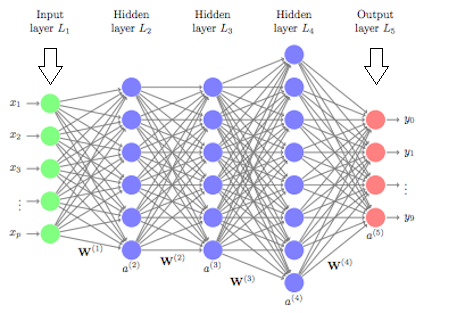
上圖就是實作時的神經網路示意圖，是一種模仿生物神經系統的結構(特別是大腦)，而這種學習的方式，最重要的特質就是它可以從資料中自動學習適當的參數。
在上圖可以看到幾個特色，各種顏色的圓圈圈叫做神經元，而最左邊綠色那排神經元叫做輸入層，中間藍色的叫做隱藏層，最右邊的紅色圓圈叫做輸出層，在層與層之間會看到很多的W叫做權重。
整理一下：
1.輸入層：負責接收資料，並將資料傳送至隱藏層。
2.隱藏層：叫做「隱藏」層是因為我們無法看見隱藏層的神經元（與輸入層或輸出層不同），看到上圖知道隱藏層可以有不只一層，所以深度神經網路就是指有複數個隱藏層。
3.輸出層：接收隱藏層的資料，並依照設定的目標輸出結果。

常用激勵函數(activation fuction)介紹

激勵函數(activation fuction)也可以稱作活化函數，那麼，為什麼要有激勵函數呢？
可以往上面看會發現權重和輸入相乘的時候，怎麼樣都還是線性的，像是最上面的非常簡單的神經網路架構，就可以看到若是沒有激勵函數的存在，最多也只是無數個權重和輸入相乘而已，這樣不管怎麼相乘或是再多的層數也脫離不了「線性」，然而，這世界是複雜的，有許多許多都是非線性的，於是，激勵函數就出場了，使得輸出和輸入脫離線性關係，做深度神經網路就會有意義了！
一言以蔽之：激勵函數是為了引入非線性！
1.Sigmoid函數
公式：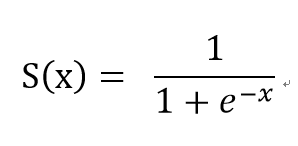

看張網路上找到的圖：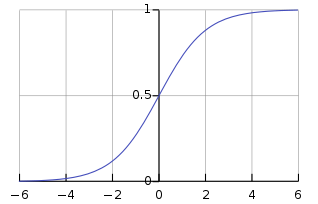

圖片來源
Sigmoid函數也可稱為羅吉斯函數（logistic function），這個function常用於分類問題。特點有以下：
(1)會將輸出範圍鎖在0~1之間
(2)恆正、嚴格遞增
(3)統計學中，函數圖像是常見的累積分布函數
(4)常用於二位元分類(Binary Classification)
(5)激活神經網路(將線性轉為非線性輸出)
讓我們自己實作一個sigmoid吧！

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
     y = 1 / (1 + np.exp(-x))
     return y

x = np.linspace(-6, 6,50) #np.linspace(開始,結束,樣本數)
y = sigmoid(x)
plt.plot(x,y)

輸出：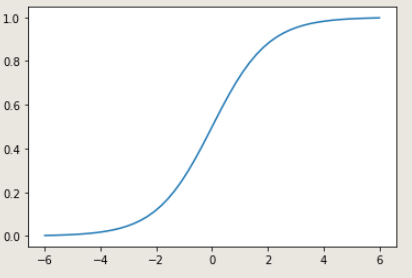

是不是覺得自己實作出來特別美呢
2.Softmax
公式：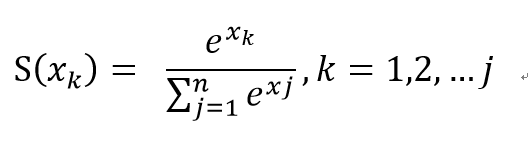

網路圖：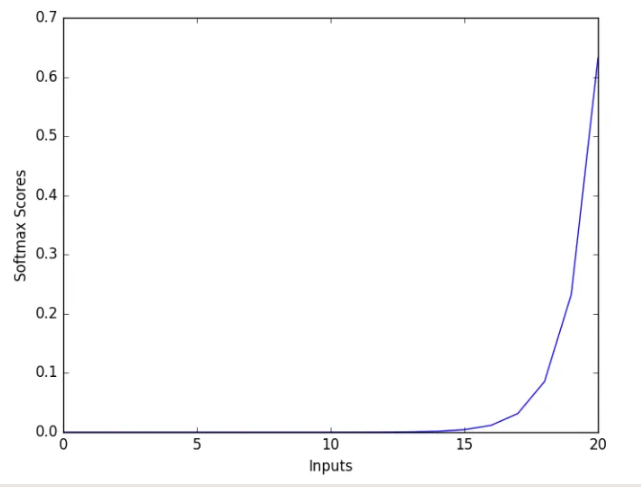

圖片來源
(1)會將輸出範圍鎖在0~1之間
(2)跟sigmoid不一樣的地方是，所有數出相加為1(所以有機率分布的感覺)
(3)統計學中，函數圖像是常見的累積分布函數
(4)常用於對重分類(Multiple Classification)
(5)用於神經網路不同層

import numpy as np
import matplotlib.pyplot as plt
def softmax(x):
    a = np.exp(x) #分子
    b = np.sum(a) #分母
    softmax = a / b
    return softmax
x = np.linspace(-6, 6,50) #np.linspace(開始,結束,樣本數)
y = softmax(x)
plt.plot(x,y)

輸出：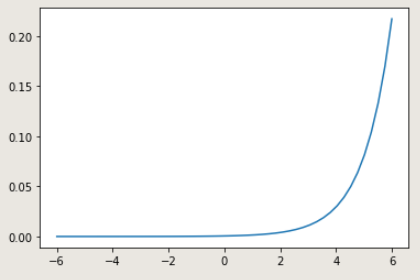

(網路圖有點鋸齒是因為他代的點比較少一些)
3.ReLU
公式：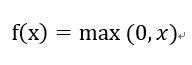

網路圖：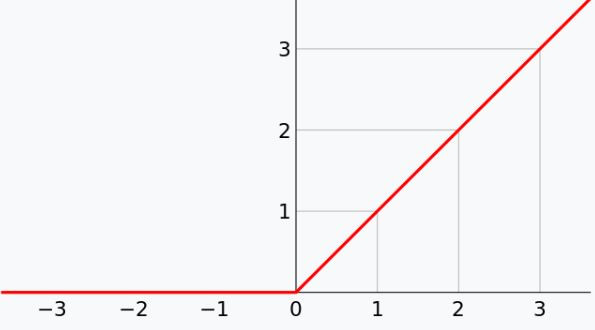

圖片來源
特點：
(1)負數輸出為0，正數輸出原本大小
(2)可解決梯度爆炸
(3)收斂速度快

import numpy as np 
import matplotlib.pyplot as plt
def relu(x):
    return np.maximum(0,x)

x = np.linspace(-6, 6,50) #np.linspace(開始,結束,樣本數)
y = relu(x)
plt.plot(x,y)

輸出：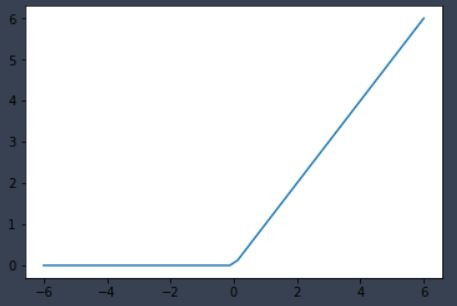

終於把它補完了，最近時間太少了，加上自己沒有庫存，都是每天花３～４個小時去整理的，這兩天會比較少，但六日會將缺失的補足的！也請有在關注我的人不要太失望了
繼續一起努力！