當我們透過第一和第二張影像經由三角測量，
獲得基於第一張影像的相機位置為原點的3D點群。

Q:你也許會問，如果有之前的流程我每兩張鄰近的影像，
都從本質矩陣去求的R|T不就能得知我的運動姿態了?

A:這個方法不能說完全錯，你也許可以獲得正確的相對方向，
但你無法確定的是第一和第二張影像之間的T1
與第二和第三張影像之間的T2的關係，
經由本質矩陣求解的T因為尺度不確定性的關係，
T1和T2的長度都是1。

所以我們想繼續推得之後相機的運動必須透過solvePnP的方法，
去找出這些3D點投影到接下來的影像中影像位置。
經由這些對應關係，去求解"這個相機"在以第一個相機為原點的世界座標位置。

讓我們先假裝忘記第一和第二張影像之間的R|t。
我們先透過之前使用到的匹配，
準備我們的參數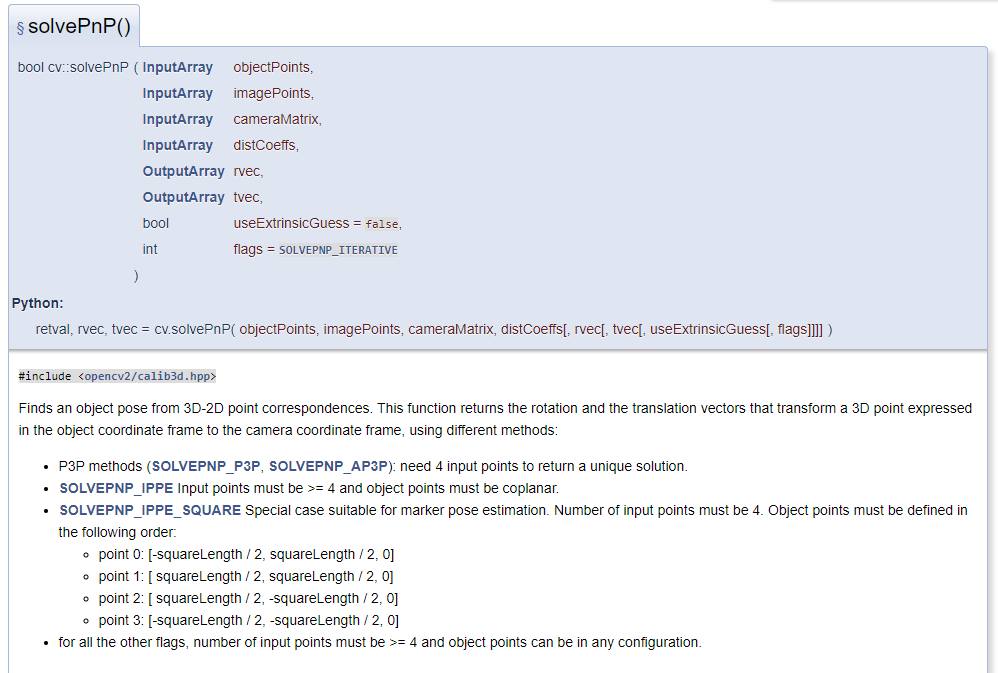

首先第一個參數會是一個vector，
我們可以將之前三角測量的齊次座標經過歸一化求出3D點，

而第二個參數是vector，
對應這些3D點的影像座標就會是當初在進行三角測量的計算時所用到的特徵點影像座標。
比較需要注意的是point3d_homo的順序會跟matches有關係，
而不是跟keypoints的順序，

換句話說當我們要推廣到第三張影像的時候，
並不是每一個point3d_homo的點都會用到
point3d_homo.col(0)這組點是否有對應，我們必需去找
ALL_good_matches[0][0]中第一組匹配的queryIdx;
與
ALL_good_matches[0][1]所有的匹配中是否有某一組匹配的queryIdx;
一致我們才能將這組點塞入配對中。
並從找到的那組匹配的trainIdx找回對應的特徵點影像座標。

第三第四組相機參數與畸變參數就從相機的校正檔讀取，
我們需要準備輸出用的R|t，
再之後的是
是否以輸入的R|t作為迭代收斂的初始值，
flag則是選擇求解PnP的解法，

std::vector<cv::Point3d> points1;
std::vector<cv::Point2d> points2;
int j = 0;
for (auto i = ALL_good_matches[0][0].begin(); i != ALL_good_matches[0][0].end(); j++,i++)
{
    cv::Mat vec4 = point3d_homo.col(j);
    vec4 /= vec4.row(3);
    cv::Point3d temp= cv::Point3d(vec4.at<double>(0,0), vec4.at<double>(1, 0), vec4.at<double>(2, 0));
    std::cout << "temp"<<temp << std::endl;
    points1.push_back(temp);
    points2.push_back(cv::Point(list_of_keypoints[1].at(i->trainIdx).pt.x, list_of_keypoints[1].at(i->trainIdx).pt.y));
}

目前這邊的points2是跟之前的三角測量的init_point_img2一樣。

cv::solvePnP(points1, points2, cameraMatrix, distortion_coefficients, PnP_R, PnP_t ,false, CV_ITERATIVE);
cv::Rodrigues(PnP_R, PnP_R2);

std::cout << "R : " << R << std::endl;
std::cout << "t : " << t << std::endl;

std::cout << "R2 : " << PnP_R2 << std::endl;
std::cout << "t2 : " << PnP_t << std::endl;

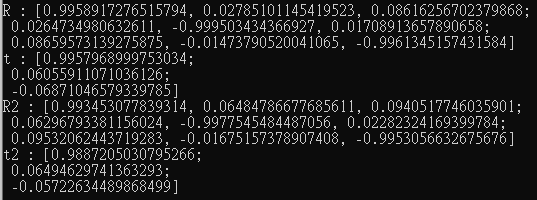
而PnP還有solvePnPRansac()的版本可以使用，
最後3D點的對應在只有特徵點的匹配下有些難找，
我在想之後的內容加入光流來尋找對應的影像座標會比較容易。