calibration後續
感恩學弟，讚嘆學弟，
就在我苦惱校正結果為何時好時壞的時候，
學弟點出了一個問題我的同一組校正影像並不是每一張都是4080X3056，
有些影像是我將手機直立所拍攝的，而軟體會自動存成3056X4080，
這會造成一些問題的是為了讓特徵點運算的速度加快，
我並不是使用原尺寸的影像，當我將兩種不同的尺寸線性縮小成640X480的時候，
兩種尺寸的變形情況不是同一種，
再者影像中心的座標X軸、Y軸也會相反，
這都會影響校正結果的收斂。

這讓我頓時有了新的方向，
我回去將每張影像旋轉成4080X3056的時候
(當然也可以透過程式自動化處理兩種尺寸的影像，自動化的進行旋轉cv::flip())，
此次得到的校正結果其校正誤差都在0.2左右，是一個還能接受的誤差。

回到今天的主題三角測量，
當我從本質矩陣(Essential Matrix)得到兩個影像之間的R|t的時候我該如何做三角測量呢?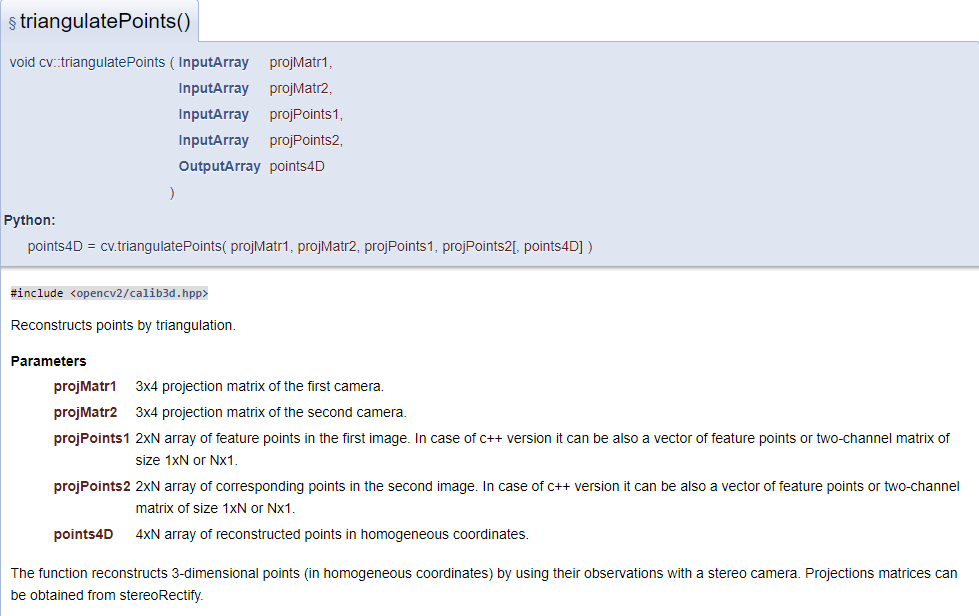

從三角測量的參數中，第三跟第四的參數不難理解，我只要將匹配的特徵點影像座標輸入進去就好，
但是第一跟第二的投影矩陣我該如何獲得呢?

首先我可以假設，第一張影像的相機座標就是世界座標的原點，因此我可以推得，
第一張相機的R|t會是一個3X3的單位矩陣表示沒有旋轉R和1X3的0位移向量表示沒有變位，
而第二張影像的相機位置就會從這個原點，經過本質矩陣得到的旋轉位移，
得到了這個以第一個相機座標為原點的第二張影像的相機外部參數，

cv::Mat Rt0 = cv::Mat::eye(3, 4, CV_64FC1);
cv::Mat Rt1 = cv::Mat::eye(3, 4, CV_64FC1);
R.copyTo(Rt1.rowRange(0, 3).colRange(0, 3));
t.copyTo(Rt1.rowRange(0, 3).col(3));
std::cout << "R : " << R << std::endl;
std::cout << "t : " << t << std::endl;
std::cout << "Rt0\n" << Rt0 << std::endl;
std::cout << "Rt1\n" << Rt1 << std::endl;

該有的參數都有了，我就可以嘗試調用triangulatePoints，
並將其結果與recoverPose得到的3D點一起比較。

cv::Mat point3d_homo;

triangulatePoints(cameraMatrix* Rt0, cameraMatrix* Rt1,
    init_point_img1, init_point_img2,
    point3d_homo);

for (size_t i = 0; i < point3d_homo.cols; i++)
{
    std::cout << "point3d_homo.col " << i << " : " << point3d_homo.col(i) << std::endl;
    std::cout << "triangulate.col " << i << " : " << triangulate.col(i) << std::endl;
    std::cout << "//--------------------------------------------// " << std::endl;
}

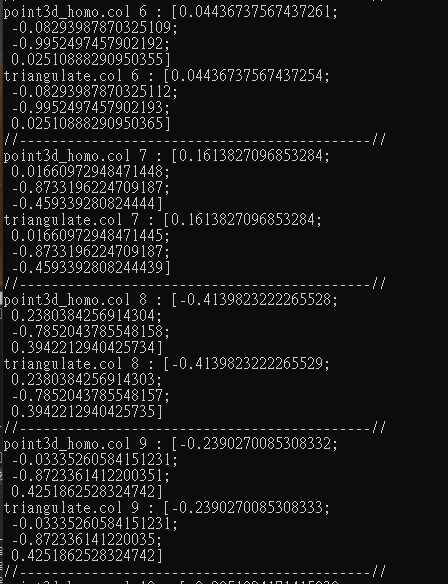
初步來看兩著者的結果是一致的，
而實際到github看recoverPose裡面在使用triangulatePoints(461~629)會發現實際情況可能沒有這麼單純，
recoverPose還考慮了在分解本質矩陣中得到的R|t有四種情況，而只有其中一種會是真實情況。
還有因為尺度不確定的關係從這裡獲得的t永遠都會是單位向量，因此單目相機中獲得的點雲都只會是比例關係，
而非現實中實際得到的物理距離。