前言

今天會透過Dynamic Programming來解Bellman Function，理解Policy Iteration的原理，並簡單介紹明天會用到的taxi環境。

GridWorld

用簡單的grid world當作例子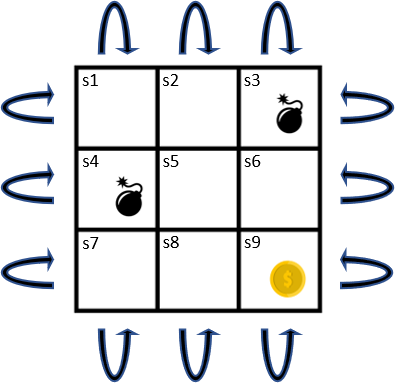

沒有Final State，所以是一種Continuing Task。
每個State皆有Left, Right, Top, Down四個行為，每個行為的轉移機率都是deterministic(確定性)的，
也就是皆為1。並會移動到下個格子。
只要該行為下個State為或的話，Reward為-1；下個State為的話，Reward為1；其餘Reward皆為0。

聯立方程式

一個很直覺的求Value Function方法就是解聯立方程式。可以把每個State的Bellman Function都列出來
()

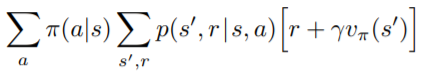
9個未知數，9個方程式，可以解聯立方程式來求

如果把設為1會發生甚麼事？該方程式無解！

Optimal Policy

我們可以從現在Value Function來得到比現在的Policy()更好的Policy()

更好的Policy指的是 for all

將每個State上的Action都往Action-Value最大的方向走，將該Action的機率設為100%，其他Action皆為0%：

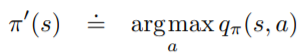
此Deterministic Action稱為greedy action

從上觀察，假如一開始為隨機策略，每個方向的機率都為25%。算完Value Function後，發現的值最大，如果現在將新的Policy裡的，其他State都不變的話，原本只有25%的Value從得到，現在100%就可以保證新的Policy可以讓的Value更大。

假如現在根據我們求出新的Action-Value Function ，發現比還要大，只要新的Policy()在上的行為改成的話，根據Bellman Function，Action-Value上的值是依據下一個State的值與Reward來決定的，所以選擇最大的Action-Value的方向可以保證下個Value Function的值比現在還大。

詳細證明可參考這裡

上面這種根據求，再用求的過程稱為Policy Iteration。

可以擴展成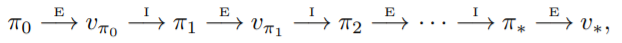

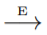• 稱為policy evaluation
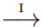• 稱為policy improvement。

通過這個過程，最後Policy會收斂，這個Policy就稱為Optimal Policy，Policy與Value Function可以寫作與，
這個Policy就是我們強化學習最後的目標，可以最大化Value Function。

現在問題來了，每次policy evaluation都要解一次聯立方程式，當我們State很多的時候非常沒有效率。
這時候Dynamic Programming就非常有用了。

動態規劃(Dynamic Programming)

我們可以用迭代的方式計算Value Function，演算法如下：

每一次迴圈都將每個State的Value往Bellman Function的解移動，迭代一定次數後就能收斂。讓Value不需要完全收斂，因為收斂的速度會隨著離解越近而變慢。

把Policy Evaluation跟Policy Improvement合再一起，稱為Policy Iteration：

policy-stable為收斂條件，只要Policy不再更新，表示已經找到optimal policy。
可以看到Policy Improvement中，的更新就是依據Action-Value Function的最大值來決定。

從下面這張圖可以看出Policy Iteration的精神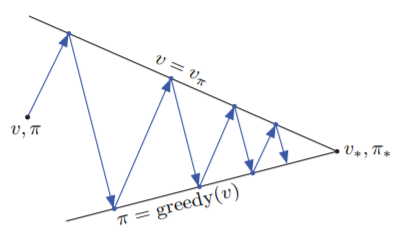

Policy Evaluation與Policy Improvement其實是相互競爭的關係，Policy Evaluation會讓之前計算的失效，而Policy Improvement也會將的值改成錯的。但是這兩個過程卻會一步步地往Optimal Function靠近，最後收斂。

這種精神在強化學習的所有算法裡都通用，稱為Generalized Policy Iteration(GPI)。

Gym

先介紹明天會用到的gym環境，明天就可以少寫一點
還沒安裝gym的記得先安裝

pip install gym

以Taxi-v2為例
先import近來，並建立環境

import gym
env = gym.make('Taxi-v2')
env = env.unwrapped # 使用更底層的操作(env.P)

再開始gym的環境前，一定要先reset()

env.reset()

可以透過render()看目前狀態

env.render()

會出現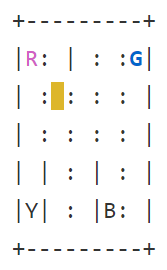

黃色是車子的位置，英文字代表乘客可能的位置或目標可能的位置，藍色英文字代表目前乘客位置，紫色英文字代表乘客的目標。當街上乘客後，車子會呈綠色。實線的部分是牆壁，虛線則是可以走的部分。
遊戲的目標就是將車子開到藍色的點，接上乘客，前往紫色的點，放下乘客。

總共有6個Action：

• 0 = 往下
• 1 = 往上
• 2 = 往右
• 3 = 往左
• 4 = 接上乘客
• 5 = 放下乘客

500個State，每個State分別表示一種情況。

可以透過指令來看

print(env.action_space.n) # 6
print(env.observation_space.n) # 500

如果要看環境的Dynamic的話，可以輸入

print(len(env.P)) # 500

print(env.P[0]) 
# {
#  0: [(1.0, 100, -1, False)],
#  1: [(1.0, 0, -1, False)],
#  2: [(1.0, 20, -1, False)],
#  3: [(1.0, 0, -1, False)],
#  4: [(1.0, 16, -1, False)],
#  5: [(1.0, 0, -10, False)]
# }

env.P為500個item的dict，每個item對應到一個state
env.P[0]印出第0個state，有0~6的action，
每個action對應到的list裡的值分別為(p(s', r|s, a), s', r, done)

• p(s', r|s, a)為轉移機率
• s'為下個state
• r為reward
• done表示s'是否為terminal state

透過step(action)與環境互動

env.step(0) # choose action 0

step(action)會回傳一個tuple，
內容為(s', r, done, info)，

• s'就是經過該action後的下個state
• r為經過該action得到的reward
• done表示s'是否為terminal state
• info為其他資訊(p(s', r|s, a)等等)

舉個例子

state為393時的情形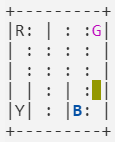

經過env.step(0)後回傳(493, -1, False, {'prob': 1.0})

render()的結果為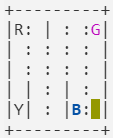

可以看到step(0)讓車子往下移動了一格。

總結

GPI的概念在之後的演算法裡都能看到，之後講到的時候會在連結回來。
明天終於要實際用code來求與，將可以看到不用寫任何rule，車子就能每次都往最正確的地方移動！