前言

Dynamic programming可以幫助我們算出Value Function，今天就來實際實做兩種Dynamic programming方法：Policy Iteration跟改良後的Value Iteration，來解決Taxi問題！

Policy Evaluation

詳細可以參考上篇

這裡直接跟著演算法實作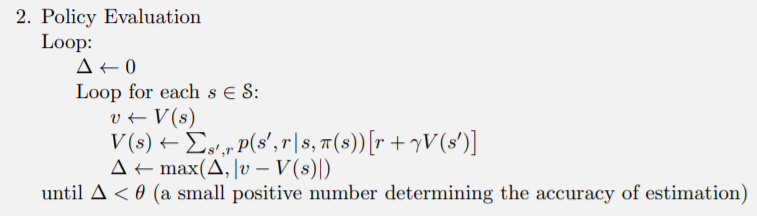

def policy_evaluation(V, policy, gamma, theta):
    while True:
        delta = 0
        for s in range(env.observation_space.n):
            v = 0
            for action, action_prob in enumerate(policy[s]):
                for prob, next_state, reward, done in env.P[s][action]:
                    if done:
                        v += action_prob * prob * reward
                    else:
                        v += (action_prob * prob * (reward + gamma * V[next_state]))
            delta = max(delta, np.abs(v - V[s]))
            V[s] = v
        if delta < theta:
            break

有幾點需要注意

• policy為(state, action)大小的array，policy[s][a]就是
• Final State的必須為0，因為我們迴圈會算到Final State，所以要加個條件式判斷如果為Final State的話V[next_state]=0
• 用v當作新的V[s]比較好算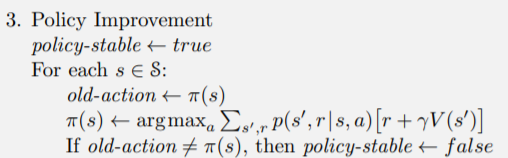

Policy Improvement

def policy_improvent(V, policy, gamma):
    policy_stable = True
    for s in range(env.observation_space.n):
        old_policy = policy[s].copy()
        q_s = np.zeros(env.action_space.n)
        for a in range(env.action_space.n):
            for prob, next_state, reward, done in env.P[s][a]:
                if done:
                    q_s[a] += prob * reward
                else:
                    q_s[a] += (prob * (reward + gamma * V[next_state]))
        best_action = np.argmax(q_s)
        policy[s] = np.eye(env.action_space.n)[best_action]
        if np.any(old_policy != policy[s]):
            policy_stable = False
    return policy_stable

• 這邊先開個空array來算
• 再用argmax求最好的
• 最後用np.eye將其他action設為0

Policy Iteration

最後就是iteration的部分，一開始的policy通常為隨機策略

def policy_iteration(gamma = 0.99, max_iteration = 10000, theta = 0.0001):
    V = np.zeros(env.observation_space.n)
    policy = np.ones([env.observation_space.n, env.action_space.n]) / env.action_space.n
    for i in range(max_iteration):  
        policy_evaluation(V, policy, gamma, theta)
        stable = policy_improvent(V, policy, gamma)
        if stable:
            break
    return V, policy

如果一開始policy不是隨機策略、又為1的話，有可能會因為policy沒有考慮到Final State，導致policy evaluation無法收斂(類似continuing task)

Taxi

實際來跑跑看Taxi環境吧
Taxi環境裡，亂放乘客下車的話reward為-10，成功放乘客下車reward為20，其餘reward皆為-1

import gym
import numpy as np

env = gym.make('Taxi-v2')
env = env.unwrapped

V, policy = policy_iteration(gamma = 0.99, max_iteration = 10000, theta = 0.0001)
state = env.reset()
rewards = 0
steps = 0
while True:
    env.render()
    action = np.argmax(policy[state])
    next_state, reward, done, info = env.step(action)
    rewards += reward
    steps += 1
    if done:
        break
    state = next_state
print(f'total reward: {rewards}, steps: {steps}')

上面是gym環境一般的邏輯，依照state選擇action，透過step(action)更新state，再根據新的state選擇action。

如果沒有寫錯的話，應該可以看到我們的車子每次做的行為都是最佳行為，因為每次行為皆有-1的reward存在，要最大化Value Function就必須走最短路徑。

Value Iteration

你可能有發現我們將設為0.99，為甚麼不設成1呢？如果將設為1並跑看看，大概跑5~10分鐘後也會得到一樣的policy。

造成跑那麼慢的原因是因為，我們一開始的policy是隨機的，一開始的Value Function會考慮所有action的值，會讓reward一直傳播下去，只要到達目標需要的step越多，reward傳遞需要的step也就越多，結果就是很難收斂。

一種解決方法就是將，這樣能強迫reward的傳播在限制的step內會趨近於0。
另一種方法就是Value Iteration，我們不需要等Value Function收斂才進行Policy Evaluation，回想GPI的圖，跟我們在Policy Improvement中的：

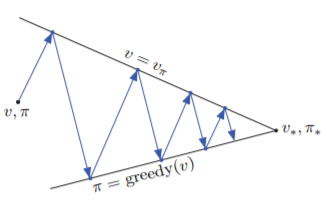
我們不一定要等完全收斂，將Policy Evaluation改成只跑一次，再直接進入Policy Improvement，就可以解決收斂過久的問題。此方法稱為Value Iteration

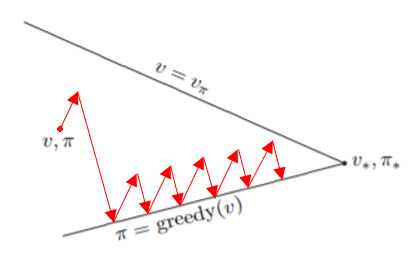
再回頭看看Policy Iteration的演算法，在Policy Improvement中找的Action當作新的，再根據求下個，等同於把policy去掉，直接找來當作下個，
也就是把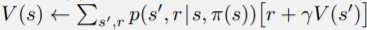 的部分
換成。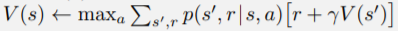

改進後的演算法如下：

我們只需要在Value Function收斂後，再求Policy，就是最佳解了。

def value_iteration(gamma, max_iteration, theta):
    V = np.zeros(env.observation_space.n)
    for i in range(max_iteration):
        delta = 0
        for s in range(env.observation_space.n):
            q_s = np.zeros(env.action_space.n)
            for a in range(env.action_space.n):
                for prob, next_state, reward, done in env.P[s][a]:
                    if done:
                        q_s[a] += prob * reward
                    else:
                        q_s[a] += (prob * (reward + gamma * V[next_state]))
            best_value = max(q_s)
            delta = max(delta, np.abs(best_value - V[s]))
            V[s] = best_value
        if delta < theta:
            break
    policy = get_policy(V, gamma)
    return V, policy
    
def get_policy(V, gamma):
    policy = np.zeros((env.observation_space.n, env.action_space.n))
    for s in range(env.observation_space.n):
        q_s = np.zeros(env.action_space.n)
        for a in range(env.action_space.n):
            for prob, next_state, reward, done in env.P[s][a]:
                if done:
                    q_s[a] += prob * reward
                else:
                    q_s[a] += (prob * (reward + gamma * V[next_state]))
        best_action = np.argmax(q_s)
        policy[s] = np.eye(env.action_space.n)[best_action]
    return policy

get_policy()只是policy_improvent()中去掉policy_stable的檢查

用Value Iteration跑跑看Taxi

import gym
import numpy as np

env = gym.make('Taxi-v2')
env = env.unwrapped

V, policy = value_iteration(gamma = 1.0, max_iteration = 10000, theta = 0.0001)
state = env.reset()
rewards = 0
steps = 0
while True:
    env.render()
    action = np.argmax(policy[state])
    next_state, reward, done, info = env.step(action)
    rewards += reward
    steps += 1
    if done:
        break
    state = next_state
print(f'total reward: {rewards}, steps: {steps}')

收斂的速度明顯比policy_iteration快了許多~~

可以比較看看兩種policy是否一致

p1 = policy_iteration(gamma = 1.0, max_iteration = 10000, theta = 0.0001)[1] 
p2 = value_iteration(gamma = 1.0, max_iteration = 10000, theta = 0.0001)[1] 
print(np.all(p1 == p2)) # True

總結

Policy Iteration跟Value Iteration可以幫助我們了解GPI的架構，但是這兩個方法都需要知道環境的Dynamic，如果不知道的話怎麼辦呢？明天介紹的Monte Carlo可以解決這個問題！