前言

昨天的樹狀結構，有一大堆的專有名詞，都有熟悉了嗎？有成功解題嗎XD，今天要進階介紹二元樹 Binary Tree

生活常識

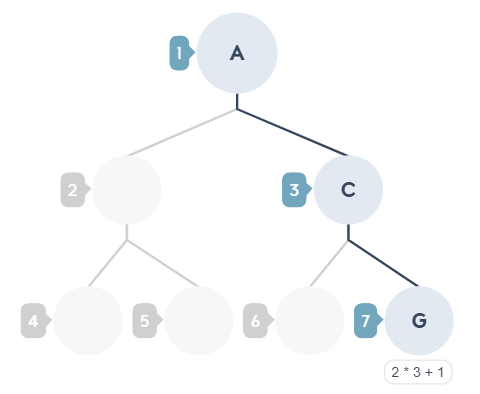
你假日的行程常常遇到選擇障礙嗎？到底要不要出去玩？如果出去玩是要找個室內環境，還是戶外呢？我們常常用要不要或是與否來做決定，當事情變成二分法的時候似乎比較簡單，而這樣的思考過程，就是一種決策的方式，透過圖表可以將思考具體化，如下圖，是不是長得很像昨天的樹呢？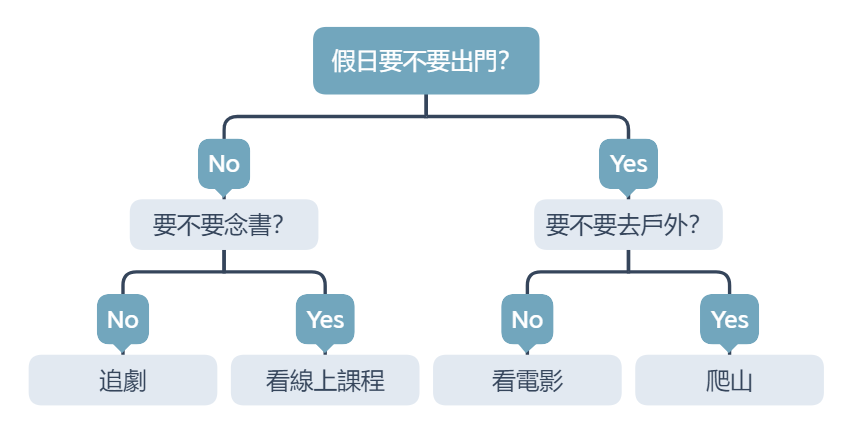

不知道大家在工作上有沒有這種經驗，遇到假民主真獨裁的主管，每每討論問題都表現出很歡迎大家提出想法的態度，但實際上卻一步步的否決大家的想法或施加壓力，然後就被迫做出自己不想要的選擇，像這種看似有選擇，但其實沒得選的情況，那麼決策就會很極端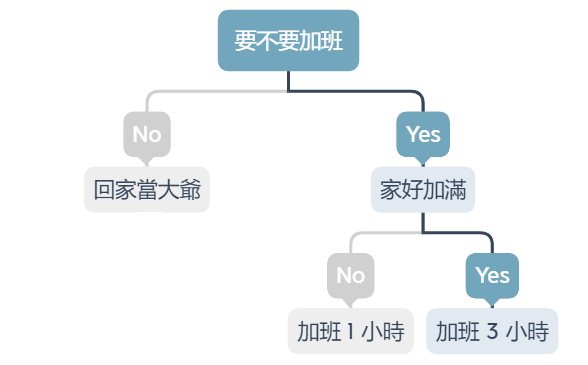

或是像球賽的機制，兩兩對決，角逐晉級資格，最後的兩隊可以競爭冠軍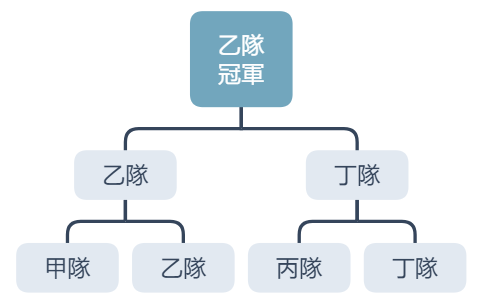

專業知識 - 二元樹 Binary Tree

跟昨天的樹不同的是，這種是與否的決策方式，最多只有兩個選項

二元樹的定義

1. 二元樹可以為空集合
2. 每 1 個節點最多只有 2 個子節點，左節點與右節點
3. 有次序關係，左節點會排在右節點之前，不能顛倒

二元樹種類

完滿二元樹(Fully Binary Tree)

一個高度(Height)為 3 的完滿二元樹，會有 7 個節點，怎麼得知的呢？
套用這個公式

完整二元樹(Complete Binary Tree)

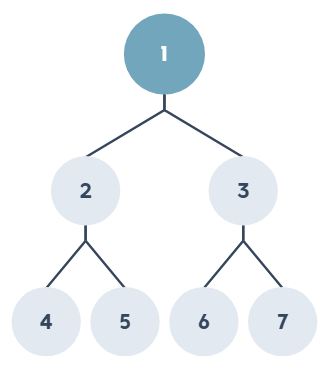
須完成以下 2 個條件：

1. 一個高度為 h ，節點數量小於，例如：一個高度(Height)為 3 的二元樹，節點小於 7 個
2. 由上到下，由左至右都跟完滿二元樹一一對應

下圖的左邊與右邊為不同的二元樹，因為二元樹的左節點與右節點有次序之分，左圖的樹，其中 6 節點，放在左邊，與上圖的完滿二元樹相同位置，所以是完整二元樹，但右圖的 6 節點卻是放在右邊的位置，所以右圖不是完整二元樹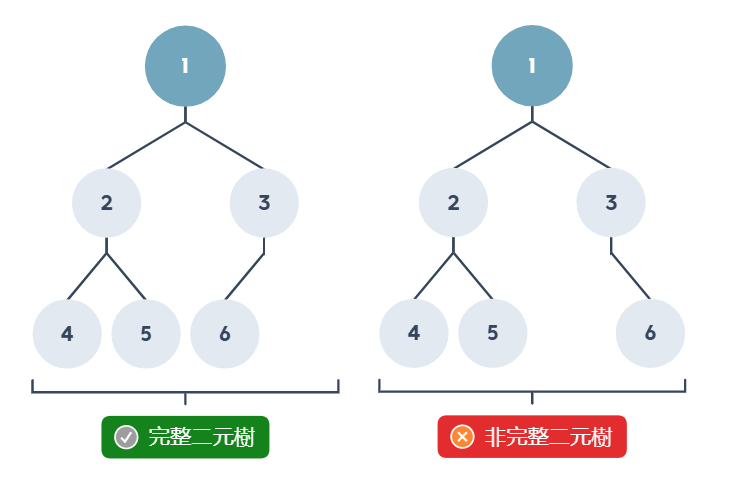

歪斜樹(Skewed Binary Tree)

當所有節點都只有左邊節點，或是只有右邊節點時，就是一棵歪斜樹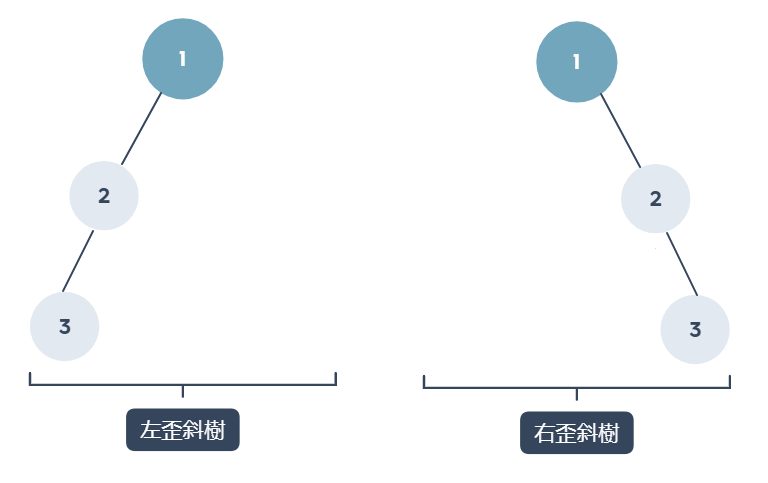

二元樹儲存方式

陣列表示法

利用陣列來儲存完滿二元樹是最節省空間的方式，如果用來儲存歪斜樹，而最浪費空間

計算節點位置：

• 陣列索引 0 的位置不使用
• 陣列索引 1 的位置為樹根
• 計算某節點(位於陣列索引 i 的位置)的左節點：2 * i
• 計算某節點(位於陣列索引 i 的位置)的右節點：2 * i + 1

使用陣列儲存完滿二元樹

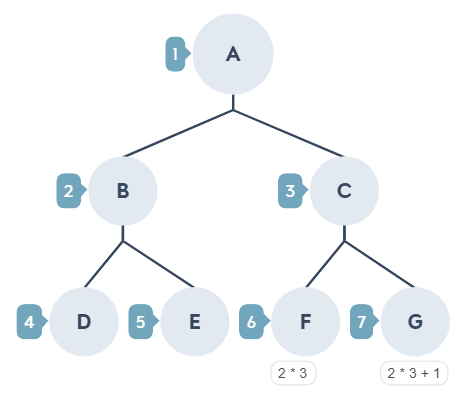
畫成二元樹：

• 陣列索引 1 的位置存放的是 A ， 所以 A 就放在根節點
• A 的左子樹，可從公式推算出 2 * 1 ( A 的索引位置) = 2，陣列索引 2 的位置存放的是 B
• C 的右子樹，可從公式推算出 2 * 3 ( C 的索引位置) + 1 = 7，陣列索引 7 的位置存放的是 G

使用陣列儲存右歪斜樹
從陣列中的資料來看，會發現有很多空間被浪費

連結串列表示法

之前我們有介紹過連結串列，裡面有提到一個節點，可以含有兩個指標，剛好在樹狀結構中就能使用指標分別指向左邊的子節點與右邊的子節點

儲存完滿二元樹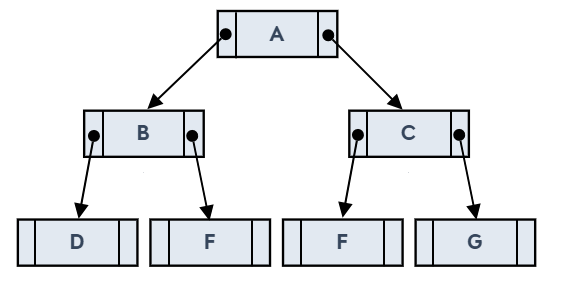

儲存右歪斜樹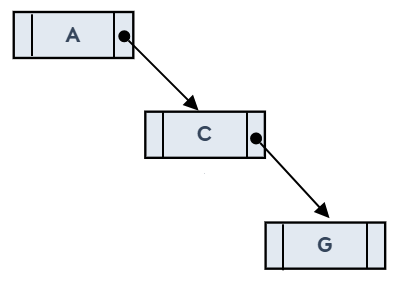

透過上圖，發現在儲存歪斜樹時，比使用陣列更節省空間，不過對於樹葉或終端節點而言，還是會有一些指標上面的浪費，因為終端節點並不包含子節點

今日小結

今天的內容似乎有點多，直接來看表格對應

項目 | 樹 | 二元樹
------------- | -------------
空集合 | 不可為空(必須有樹根) | 可為空
分支數量 | 不限 | 介於 0~2 之間
次序 | 沒有次序 | 有次序 (左節點與右節點)

今日謎題

小花發現了一個神祕種子，儲存在陣列裡面，聽說把種子撒下去會長成漂亮的二元樹，請問你能發現樹葉中暗藏什麼訊息嗎？

昨日解謎

謎題說明：要驗收一下大家對於樹狀結構的了解

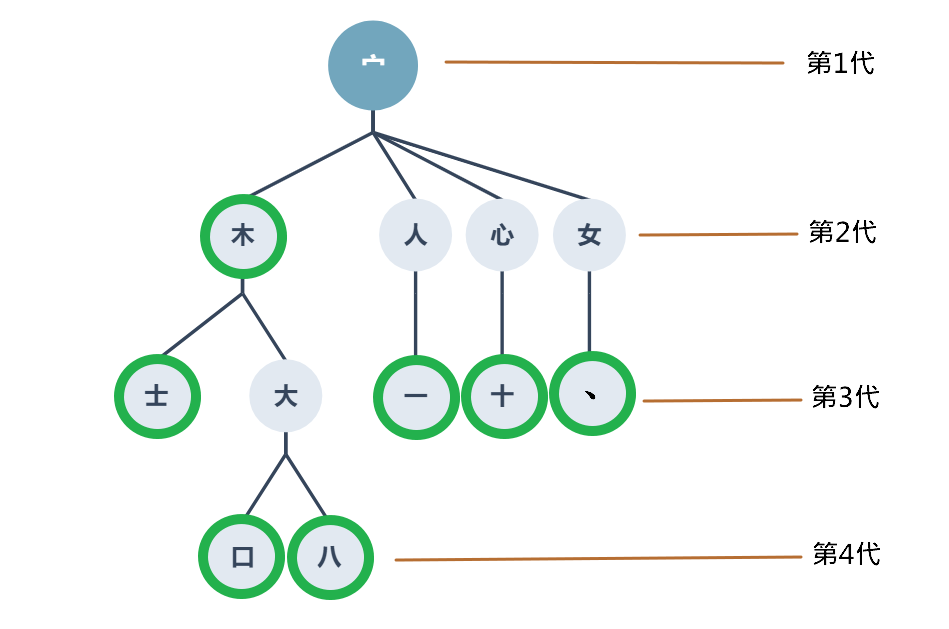
• 家族第 2 代，且生了 2 個小孩
  這一題使用到樹狀結構中階層(Level)的觀念，家族組織圖中，第 2 代分別有：木、人、心、女，其中只有木生了 2 個小孩(士、大)

• 沒有生過小孩的人
  這一題使用到樹狀結構中終端節點或樹葉節點(Terminal)的觀念，指的是該節點下沒有子節點，也就是沒有生小孩的人有：士、口、八、一、十、、

將木、士、口、八、一、十、、 這些筆劃組合起來，就會得到樹這個字囉！

樹