前言

了解如何透過陣列與串列來儲存二元樹之後，接著要進一步了解，如何讀取二元數，根據讀取的順序不同，又分為中序、前序與後序走訪，今天會從中序走訪開始介紹

生活常識

計算機算是蠻常見的小工具，當我們要進行運算時，通常會先按一個數字，再按加/減/乘/除，然後再按另外一個數字，計算機畫面就會出現計算結果

圖片來源:https://www.pexels.com/zh-tw/photo/53621/

例如當我們做加法的時候，首先會準備兩個數字 3 和 5，然後會先在計算機按 3 再按 + 號，最後按 5 ，計算機畫面就會出現 8 ，而當我們在表達一個加法的時候，會將兩個數字分別放在加法符號的左右兩側，公式會長這樣 3 + 5，這是我們很熟悉的四則運算，那這個放在中間的四則運算就像是樹根，而左右兩邊的樹字就像是左右節點：< 運算元1 > < 運算子 > < 運算元2 >

專業知識 - 二元樹走訪 Binary Tree Traversal

通常看到乘法或除法，會習慣優先處理，因為乘法與除法有比較高的優先權，而括號也可以用來標記哪些資料要優先處理，但如果以電腦的方式去判讀中序式的公式，那處理起來會非常複雜，有很多額外的條件要另外處理

如果透過前序或後序的話，就不會出現括號，乘法與除法也都會按照優先順序先排列好，所以電腦處理起來會方便許多，也就是將算式轉乘二元運算樹以方便電腦運算，那麼如何產生前序與後序走訪的結果呢？就必須先仰賴中序式的算式來畫出二元運算樹

走訪定義

讀取每個節點一次

走訪方式

左子樹的順序一定會大於右子樹，重點就在於根節點的位置在哪邊

• 中序走訪(Inorder)：順序：左子樹 → 根節點 → 右子樹，根節點在中間，結果為：左根右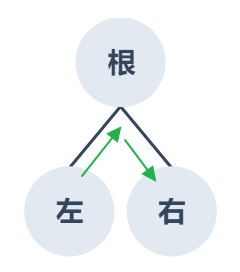
  

• 前序走訪(Preorder)：順序：根節點 → 左子樹 → 右子樹，根節點在前面，結果為：根左右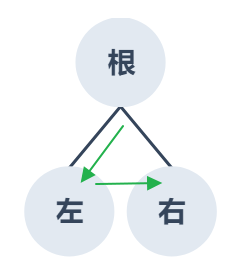
  

• 後序走訪(Postorder)：順序：左子樹 → 右子樹 → 根節點，根節點在後面，結果為：左右根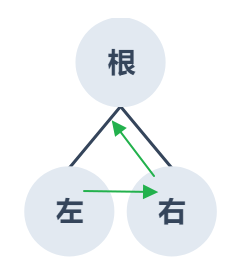
  

中序走訪 Inorder

今天會講中序的部分，前序與後續明天會在說明，下圖右方是四則運算以的二元樹來表達，其前序走訪結果為：3 + 5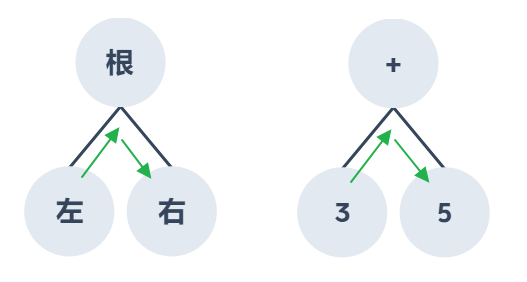

中序練習

我們一起來看看以下這棵二元樹的中序走訪結果為何，雖然知道順序：左子樹 → 根節點 → 右子樹，但看到下圖一時之間好像會有點不知道該如何下手，但其實推算出來的走訪結果會是我們日常生活中看到的運算式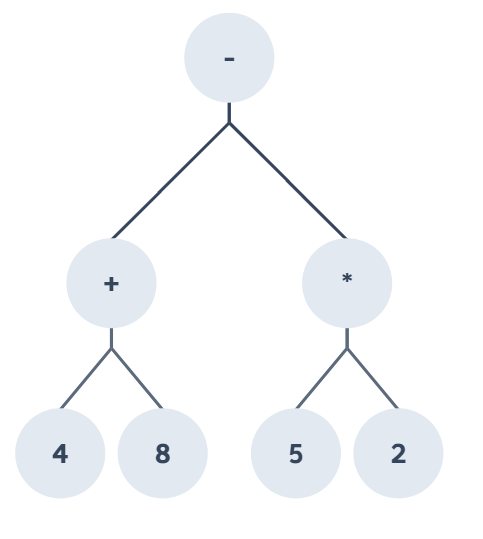

首先我們先找到樹根的左子樹，發現這個左子樹下面又包含了左節點與右節點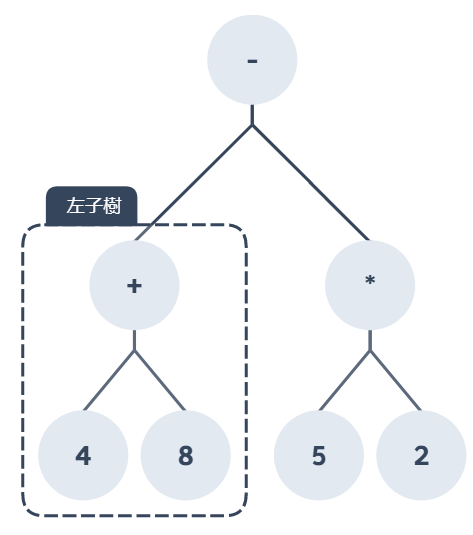

依照順序：左子樹 → 根節點 → 右子樹讀取這個子樹就會得到：4 + 8，這樣左子樹的部分就處理完畢了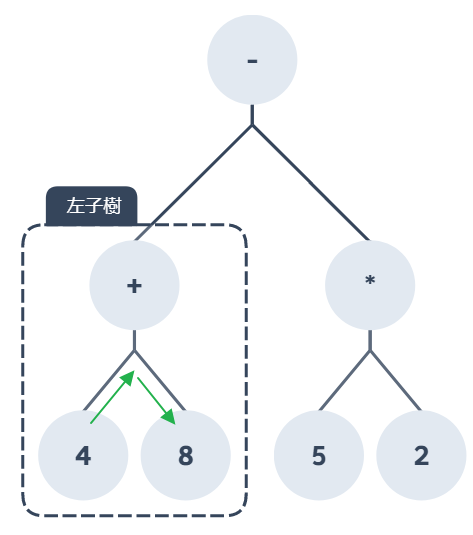

再來要處理樹根，就會得到：4 + 8 -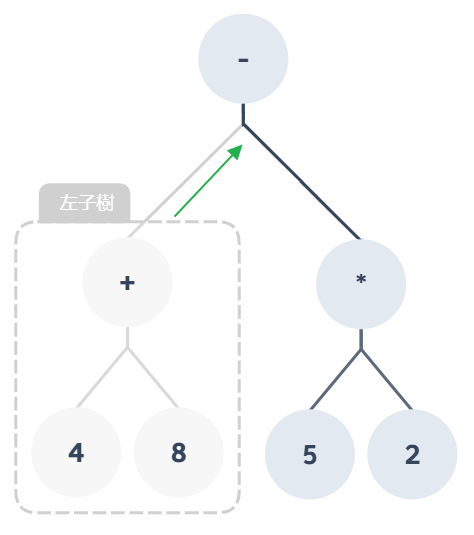

最後是右子樹的部分：依照順序：左子樹 → 根節點 → 右子樹讀取這個子樹就會得到：4 + 8 - 5 * 2，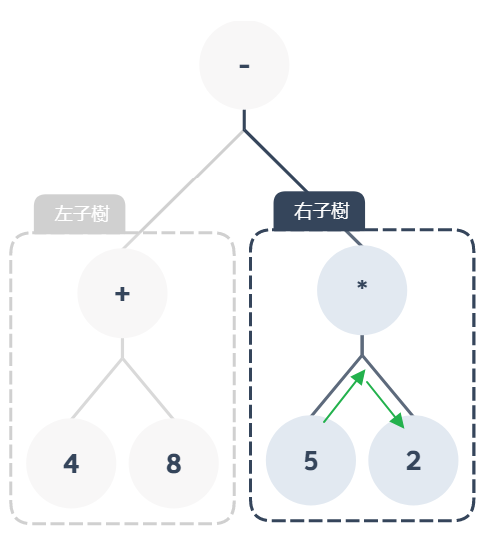

所以中序訪問結果為： 4 + 8 - 5 * 2，而你可能你好奇中序式要如何轉換成二元樹的？這個部分會在明天說明喔！

今日小結

中序訪問的結果大多是人類思考的方式，例如看到4 + 8 - 5 * 2就可以馬上計算出結果，但先預告一下明天的前序與後序的訪問結果是給電腦看的，所以我們會看不懂XD

今日謎題

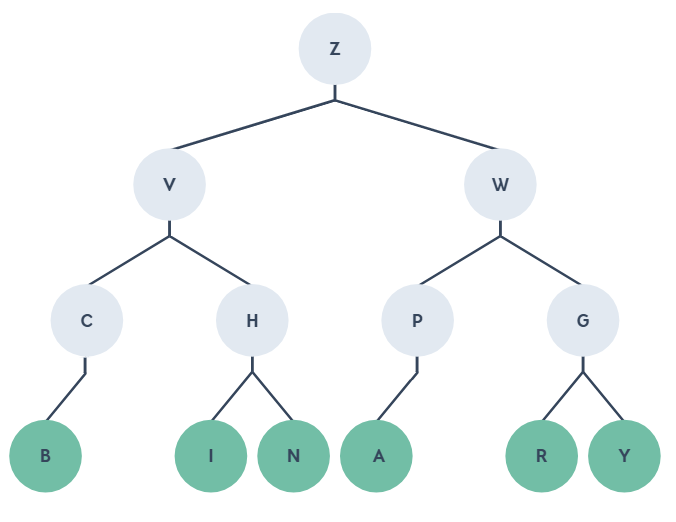
小美的男朋友是一位工程師，他用了二元樹的中序走訪寫了一封情書要給小美，但小美收到後表示她看不懂，請問你能幫助小美嗎？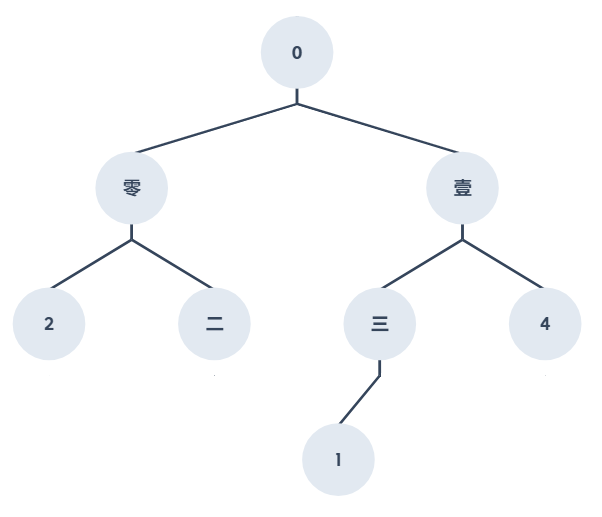

昨日解謎

謎題說明：需要了解二元樹如何以陣列表示，並根據陣列畫出二元樹，並找到該樹的樹葉節點(終端節點)，即可發現樹葉節點有：B、I、N、A、R、Y，即可組成 BINARY 這個單字，你答對了嗎？