今日kata

原始題目如下:(6kyu)
As the name may already reveal, it works basically like a Fibonacci, but summing the last 3 (instead of 2) numbers of the sequence to generate the next.
So, if we are to start our Tribonacci sequence with [1, 1, 1] as a starting input (AKA signature), we have this sequence:

[1, 1 ,1, 3, 5, 9, 17, 31, ...]

You need to create a fibonacci function that given a signature array/list, returns the first n elements - signature included of the so seeded sequence.
Signature will always contain 3 numbers; n will always be a non-negative number; if n == 0, then return an empty array.

翻譯:
Tribonacci數列的規則是:

• 第四項是第一項+第二項+第三項之和，同理第五項是第二項+第三項+第四項之和
• 第四項開始，每一項是前三項之和

根據給的陣列signature，求出完整的Tribonacci數列(前n項)

範例:

tribonacci([1,1,1],10) ----> [1,1,1,3,5,9,17,31,57,105]
tribonacci([0,0,1],10) ----> [0,0,1,1,2,4,7,13,24,44]

構想&解法

function tribonacci(signature, n) {
  if (n < 4) {
    return signature.slice(0, n)
  }
  while (n > 3) {
    let len = signature.length
    signature.push(signature[len - 1] + signature[len - 2] + signature[len - 3])
    n--
  }
  return signature
}

和Fibonacci數列(每一項是前兩項之和)很像，Tribonacci數列的規則是每一項為前三項之和。當所要回傳的數列元素數量小於4時，代表signature即為結果。
反之使用while loop，依序push增加signature的元素。

signature= [0,  0,  1]
//          n0  n1  n2
//                      n3----->每次loop所要計算的
// n3= n0 + n1 + n2 = n2 + n1 + n0
// len= signature.length 陣列長度
//    = signature[len - 1] + signature[len - 2] + signature[len - 3]

例如當n=10時，signature總共要增加7次元素(10-3=7)，陣列的前三項題目已經給，不用算~ 於是設定while的執行條件為n>3，每次push完新元素，n--。最後signature陣列即為所求。

其他解法觀摩

function tribonacci(signature,n){  
  for (var i = 0; i < n-3; i++) { // iterate n times
    signature.push(signature[i] + signature[i+1] + signature[i+2]); // add last 3 array items and push to trib
  }
  return signature.slice(0, n); //return trib - length of n
}

簡潔多了...不管n>3或n<=3，一律使用slice(0,n)，回傳signature陣列!
不用另外判斷n，也不用再宣告一個len變數!

整理用法

費氏數列

和Tribonacci很像的費氏數列，即第三項開始為前兩項之和。
費氏數列是常用來解釋Recursion(遞迴)的經典範例之一，另外還有階乘(n!)。

遞迴是把一個問題拆分成好幾個小的獨立問題。常見就是把規律 重複執行的部分抽出來處理，而函式的遞迴指的就是自己呼叫自己。

摘自The 2:00AM Javascript Blog About: Recursion. Yes, A.M.

有種全面啟動的味道(?)　很像一個無底洞，所以特別要小心注意終止條件是不是有給對...

另外也補上function的架構: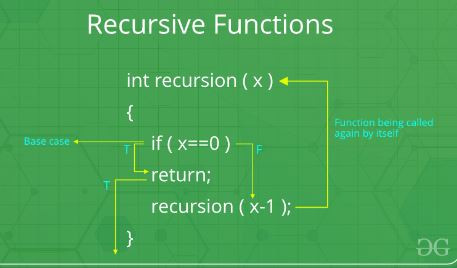

圖摘自geeksforgeeks:Recursive Functions
會有一個Base case用來判斷繼續拆解function或是跳出的條件!

所以如果像費式數列需要求最後的數字為何，用遞迴解法如下:

// F(n)=F(n-1)+F(n-2)
// F0=0, F1=1
function fibonacci(n){
    if(n<=1) return 1;
    return fibonacci(n-1)+fibonacci(n-2);
}

拆解求費氏數列index=5的元素

• 第一層fibonacci(5)
  • n>1，返回fibonacci(4)+fibonacci(3)
• 第二層fibonacci(4) + fibonacci(3)
  • fibonacci(4)=fibonacci(3)+fibonacci(2)
  • fibonacci(3)=fibonacci(2)+fibonacci(1)
• 第三層fibonacci(3)+fibonacci(2) & fibonacci(2)+fibonacci(1)
  • fibonacci(3)=fibonacci(2)+fibonacci(1)
  • fibonacci(2)=fibonacci(1)+fibonacci(0)
  • fibonacci(1)=1

以樹狀圖的拆解: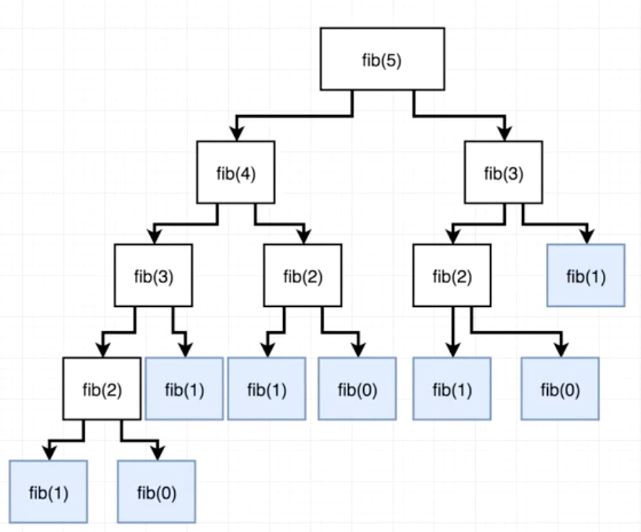

圖摘自(Diagram from Stephen Grider’s “The Coding Interview Bootcamp“ course on Udemy.com)

以上為今日分享的內容，若有錯誤或是建議，請再隨時和我聯繫。