上篇介紹了實驗設計，
這篇就希望簡單地介紹一下推論統計。

一般來說我們在生活上常聽到的統計都是「敘述統計」，
比如說平均值、標準差、PR值，
這些都屬於敘述統計的範疇，
他的核心重點是利用統計值，
去描述目標族群所形成的「分佈」的各種性質。

統計分佈的概念有點抽象，
定義上來說，他是指一個變數，他所有可能的值及對應的機率長怎樣。
比如說一個骰子，在每一面出現的機率都是公平的情況來說，
他可能的數值和對應的出現次數就長這樣：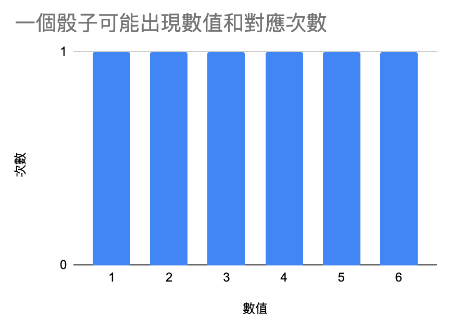

如果把對應的次數除以骰子的可能性的面數（即為6)，
就可以推出每面骰子的機率：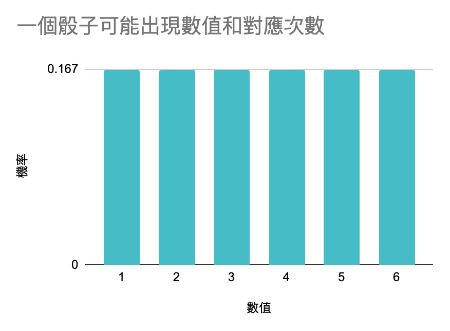

當今天同樣的骰子有兩個，我們要去算他們的和的時候，
他可能的和以及能產生該數值的面的組合的數量會長這樣：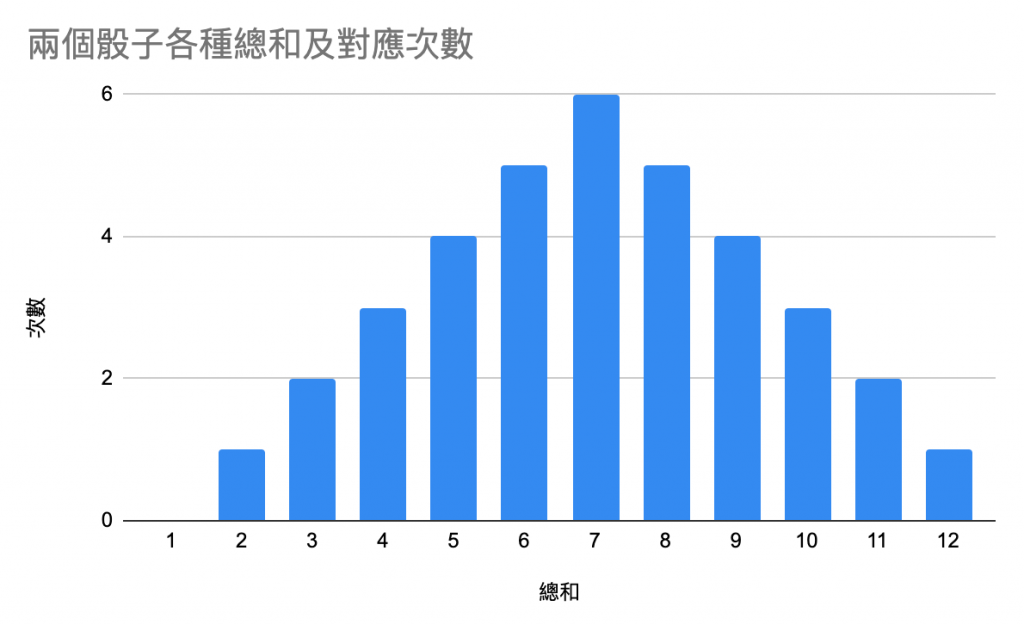

同樣地把各總和值的組合數除以總組合數，就可推出機率：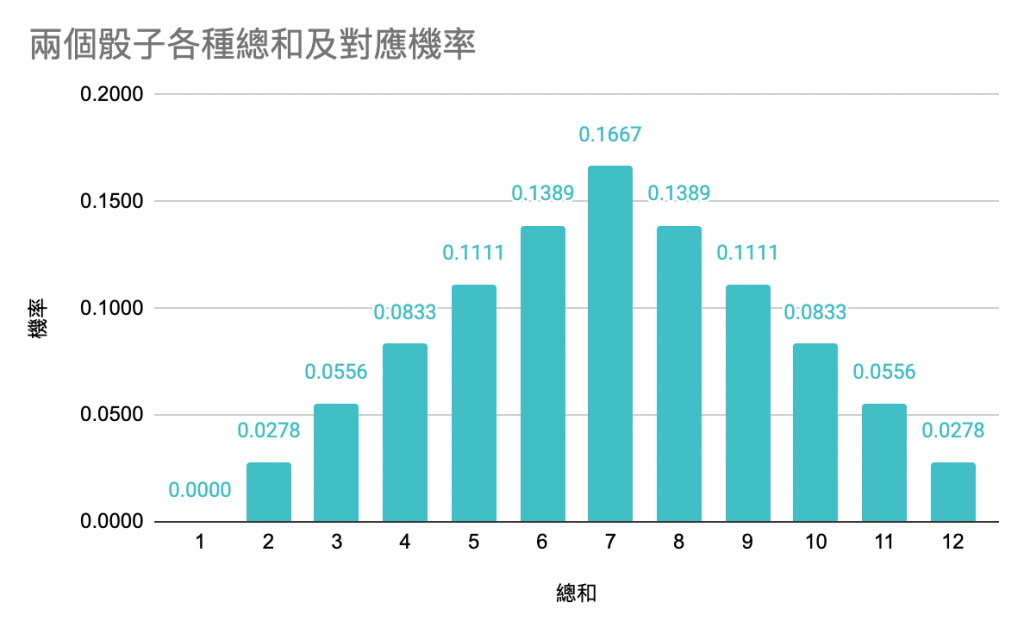

上面這個就是骰子的和（也就是這裡的變數）所形成的分佈。

統計上有很多從機率理論推導出來的分佈，
最常聽到的就是常態分佈（高斯分佈或Z分佈）。
但除了高斯分佈之外還有很多其他分佈，像是t分佈和F分佈。
他們各自用來描述不同的東西，
這個我們後面提到統計檢定會在略提一下。

推論統計則是基於各種統計分佈，更進一步去做推論分析。
他的基本精神就是去看一件事情的發生，
在一個統計分佈上是不是最極端的情況，
這稱之為統計檢定。

例如前面提到的AI建議文章的例子，
我們可以讓受試者根據有用程度打分數
（假設各項問題加在一起總分100分），
然後去看讀AI推薦文章的實驗組
和讀隨機文章的對照組，
這兩者的有用度分數差異，
藉此評測AI的推薦是不是真的有幫助。

那到底要怎麼樣才能稱之為「有差異」呢？

在推論統計上，常用的標準就是去看這個差異程度的機率值（P Value, P)，
是不是在一個相對應的統計分佈上，屬於極端的5%，
這稱之為差異「顯著」，這個0.05稱之為「顯著水準」，
常用「α（Alpha)值」來描述。

也會有人用「95%信賴水準」，來表達同樣的意思。
這個描述的意思就是說，一個變數的數值
那個統計分佈之中，
有95%的機率會落在一個範圍之中（該範圍也稱之為信賴區間），
如果出了這個範圍，就代表有什麼貓膩這個狀況很少見。

以上面的AI推薦文章的例子來說，如果算出來P=0.012，
而α值為0.05，則P=0.012 < 0.05。
就代表這兩組結果是有顯著差異的，我們就可以以此推論，
AI推薦的文章比隨機的文章好。

5%只是一個常用的標準，也有人會用更嚴格的1%
或是偶爾會有更鬆散的10%之類的標準。
畢竟標準是人訂的，你說出P值是0.051跟0.05真的有差這麼多嗎？
這個真的也很難說。

學術界也一直有在討論P值讓有些學術研究淪為對數字的追求，
為了要追求顯著，開始用各種各樣的方式修改實驗或多做各種處理，
失去了研究本身探究的精神。

這件事情相關的討論，
有興趣的人可以參考這篇的討論囉！

下篇開始我們就更正式一點地介紹統計檢定跟一些人機互動常用的統計檢定法吧！

註：本文第一版對於P值跟α值的描述有些不正確，現在已經修正。
強烈推薦有興趣細讀推論統計的人，參考以下這篇：
https://mropengate.blogspot.com/2015/03/hypothesis-testing-p-value.html