堆積也是資料結構的其中一種,也是一個完整的二元樹,而堆積的特色就是最大的數值會放在樹根,或是最小的數值會放在樹根,所以樹根會是最大值或最小值,接著我們就可以使用堆積排序法,將資料由大至小或由小至大排序完成
喝飲料的時候常常可以觀察到,有些東西會沉在杯底,例如珍珠,有些東西則會浮在飲料上面,像是冰塊或水果切片,而根據物品的體積或密度,可以推得它們在水杯中的固定的常態分佈和固定的順序,繼續丟入冰塊,冰塊只會浮在水面,不會沉下去
圖片來源:https://unsplash.com/photos/Q4Ha5yEzb9E
你有聽過重要緊急四象限法則嗎?通常在一天內,我們需要處理很多事情,除了吃喝拉撒睡,還要認真工作或認真念書,有時候忙起來真的會當機,不知道到底該處理哪一件事情才好,本來不急的事情因為規畫不當,變成非常緊急,或是非常緊急的事情或沒有趕緊處理而造成大麻煩的事件也層出不窮,可能就是時間管理上面需要做一些調整,而重要緊急四象限法則可以協助我們找出事情的優先順序,讓我們清楚接下來要優先處理哪些事情
圖片來源:https://www.pexels.com/zh-tw/photo/3760810/
資料結構的堆積會將資料按優先順序排列,讓我們可以清楚知道現在最急或最不緊急的事情有哪一些,讓我們一起來認識認識吧
堆積在之前的資料結構的部份並沒有介紹到,所以先來介紹一下什麼是堆積,有了基礎觀念之後再來認識堆積排序法,堆積是完整的二元樹,數值的排列分為兩種:最大堆積樹(Max-Heap)與最小堆積樹(Min-Heap),不論是哪一種,當堆疊中有數據被新增時,根據此數據的大小,會被調整到它應該出現的位置,這就是堆積的特性,就像上述水杯中的物品一樣,會根據某些條件,出現在它應該出現的位置
最大堆積樹(Max-Heap)
樹根為最大值,所有節點的值都會大於等於子節點的值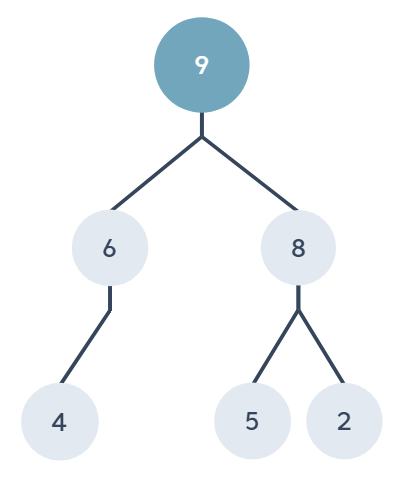
最小堆積樹(Min-Heap)
樹根為最小值,所有節點的值都會小於等於子節點的值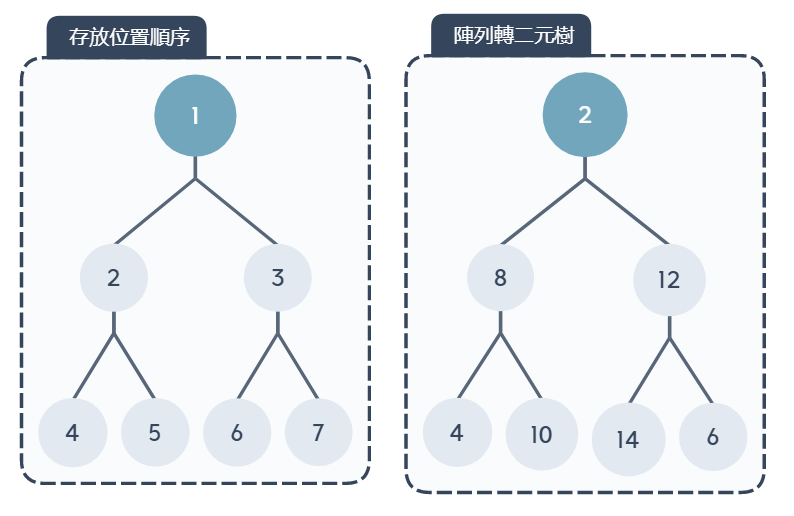
有一顆二元樹 2, 8, 12, 4, 10, 14, 6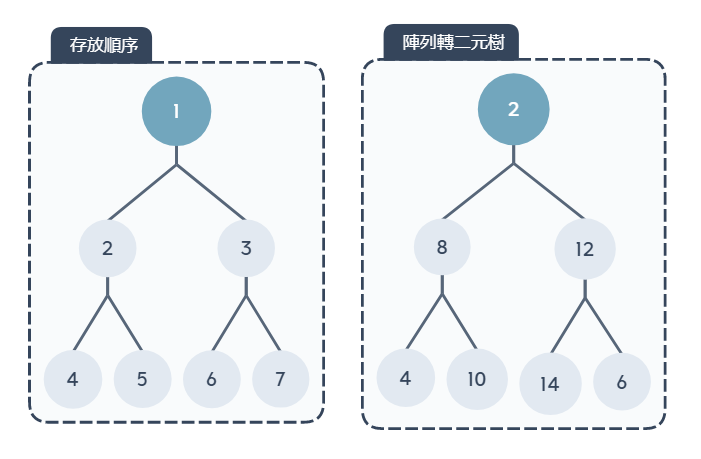
將二元樹轉成最大堆積樹,子點節與樹根節點比較大小,較大者要與樹根節點交換位置
例如位置2的子節點裡面存放的數值是 8,要與樹根節點的數值 2 相比,8 大於 2 ,所以位置要交換,接下來就逐一檢查每個位置的子節點與樹根節點的大小是否需要交換位置,詳細步驟如下圖
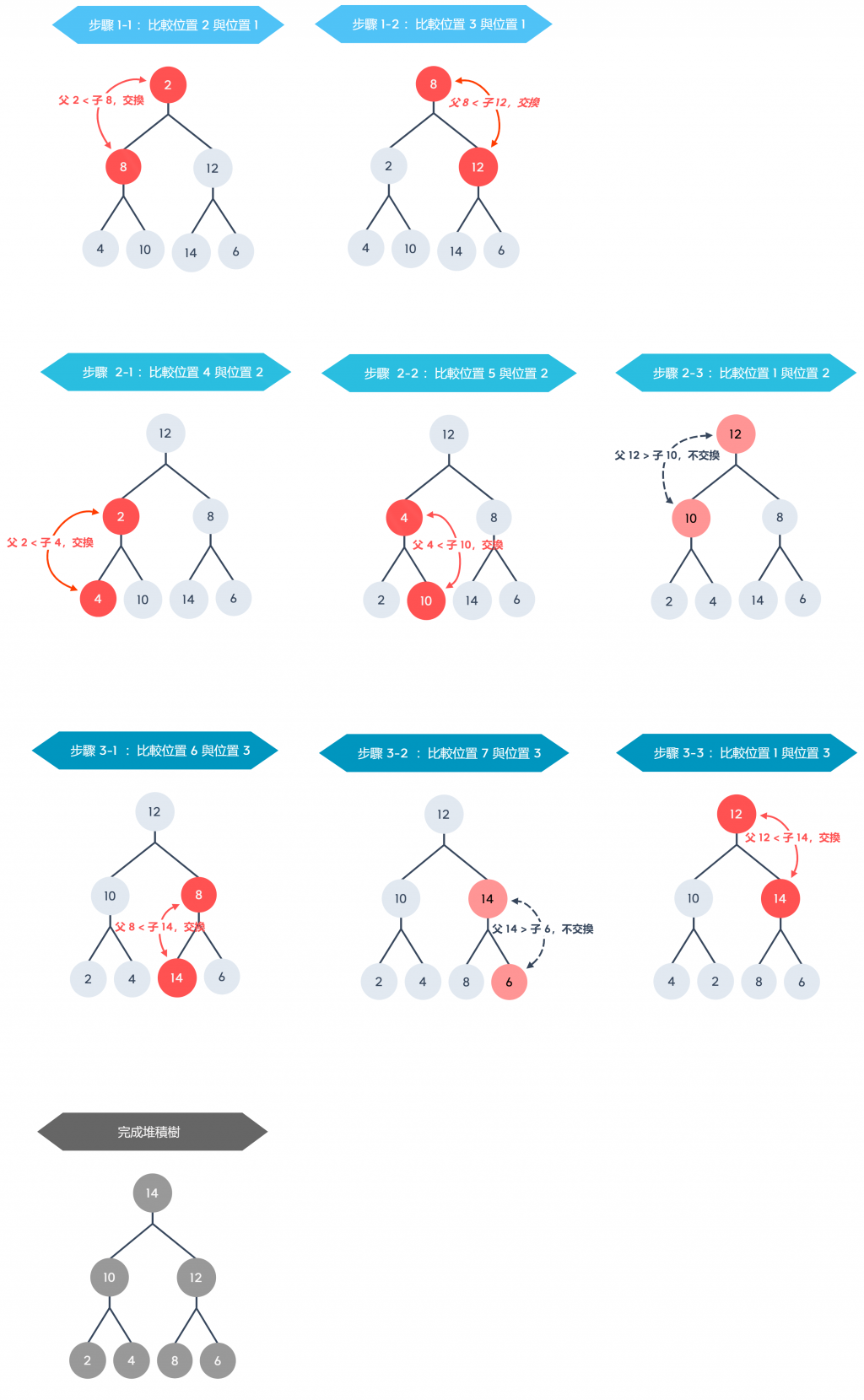
在準備好最大堆積樹之後,請執行以下步驟:
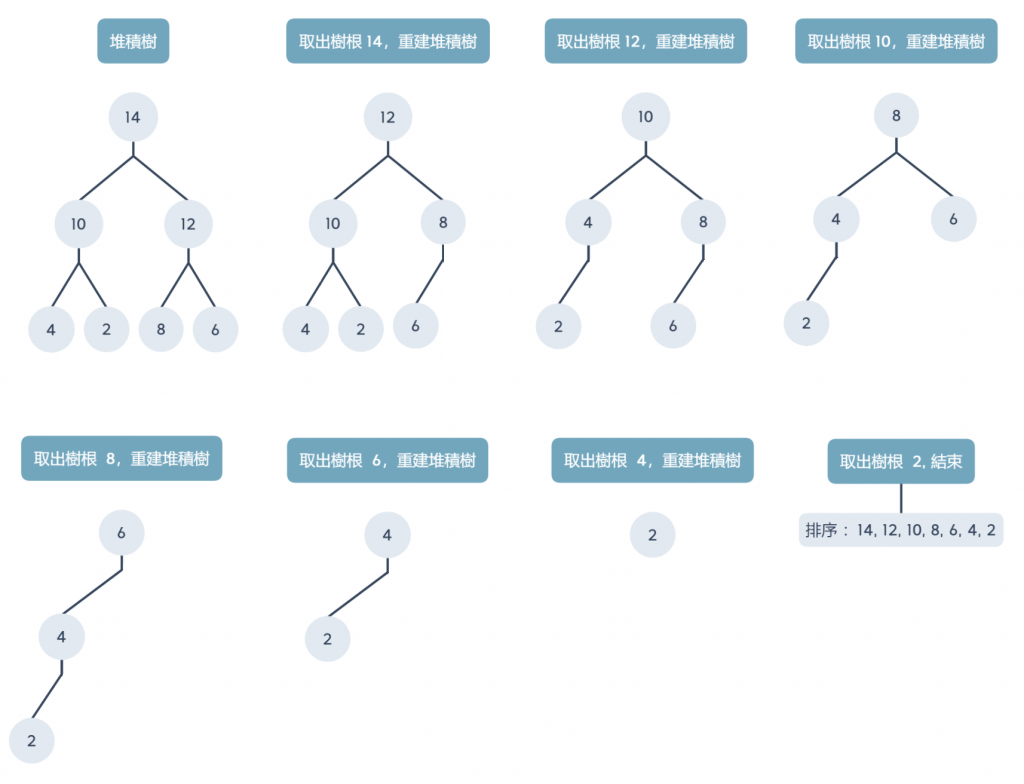
所有情況下時間複雜度皆為 O(n log n),數字有 n 個,就要取出 n 次,樹的高為 log n
堆積排序法速度雖然也很快,但這種樹狀結構在實務上是不是方便維護,也是一個需要考量的問題,高等排序法就介紹到這先告一段落囉!
聽說蒐集到四顆神秘的寶石可召喚神龍許願,首要任務是找到下列單字中的神祕訊息:
Hope
Energy
Agile
Power
每個單字裡面有一個最重要的字母,請問你知道這個單字是什麼嗎?
謎題說明:將 4, 2, 3, 4, 5, 3, 4, 5,以合併排序法由小至大排列排序,在過程中,有 2 個節點中,有存在 4 個數字,而 4 個數字剛好可以構成一個 4 拍的音節,所以可以觀察出 2 3 4 4 與 3 4 5 5,在套入到提示中的問號,就可以得到 5531 2344 3455 5353,歌曲就是火車快飛,你答對了嗎?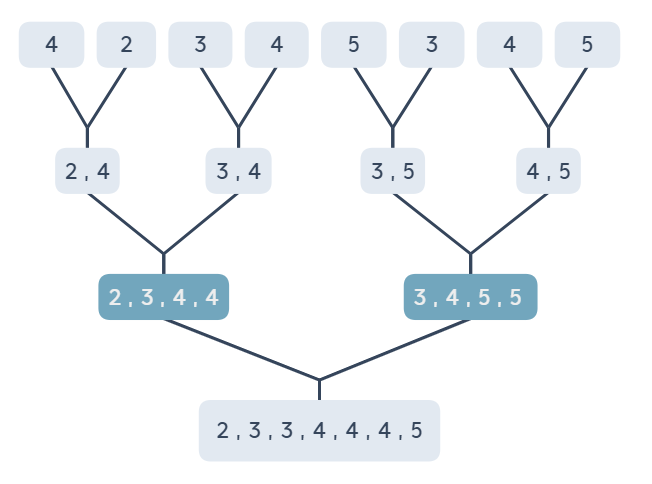

抱歉 我詳讀您的文章發現有些疑點
1.二元樹 轉成最大堆積樹的部分
步驟3:比較位置4與位置2之後 為何值2(位置2)與4(位置4)的值沒有互換?(最後應4在上,2在左下)
步驟5-1 比較位置6與位置3後,為何沒有比較位置7與位置3的步驟而直接跳到步驟5-2?
麻煩確認一下 感謝
抱歉抱歉有筆誤,謝謝您留言讓我有機會做修改~
想請您幫忙看看,修改的內容有沒有問題,謝謝~
小菜
不用道歉啦 因為您寫得好 我才特別研讀 才會抓到一些小錯誤
題外話還是感謝您特地專程寫這個題目 受益良多 感謝