在數學課本中，最早引導學生思考「抽象概念」的練習是「正數和負數」。接在負數後，會開始運用文字式的代數來取代數字，此時的目的是練習「抽象化」。

抽象化

• 定義：分析事物或表象，進而掌握特定要素、對象或性質。
• 目標：歸納出共通的性質
• 例如：
  • 將 1, 3, 6, 10, 15... 表達成 n(n+1)/2
  • 不可分割的質數即為「數的本質」
  • 生活中在「整理」將事物分類，給予命名的動作，即為抽象化的過程。例如將馬、海豚、鴿子、烏鴉分類成「哺乳類」與「鳥類」。
• 然而，若隨意分類並命名，達到「似是而非的抽象化」，反而會蒙蔽雙眼，讓我們無法看見事物的本質。
• 在日常生活中，將每天接觸的五花八門的複數事物中，進行整理與分類，並嘗試歸納本質，就是很好的抽象化練習。可以鍛鍊出「分析」的能力。

模型化

• 目標：把複雜的現實簡化成單純的模型。
• 舉了一個神奇的例子，某本暢銷書將「人生的運氣」化成微分方程式 d x 運氣 / d x 時間 = k x 運氣 - a x (運氣)^2 + sin(時間)，來代表「運氣會隨時間產生怎樣的變化」 ，從此公式中
  • k x 運氣 - 運氣愈好，愈容易形成良性循環
  • a x (運氣)^2 - 樹大招風後，也容易導至負面因素
  • sin(時間) - 上下波動的景氣循環
  • （我讀了啥？？？？）
• 根據某項假設，把對象簡化，此時會刪去許多影響因素，而訣竅就在思考何者該保留、何者該刪去。

圖論

• 由點和兩點之間的連線所構成，例如生活中的捷運路線圖
• 圖論的源起：柯尼斯堡七橋問題，「假設可以從任何一點出發，在七座橋都各走一遍的前提下，是否有辦法回到出發點」。
• 展示此命題為否的證明過程，得知必須有「偶數」的條件。
• 在進行證明時，無視土地形狀、面積、橋的方向與長度，只留下點和兩點之間的連線。用這個過程來表達「模型化」就是「把複雜現實單純化」。

應用討論

情境：有 6 個人 x 6 種會議，要用最有效率的方式來安排會議的時程

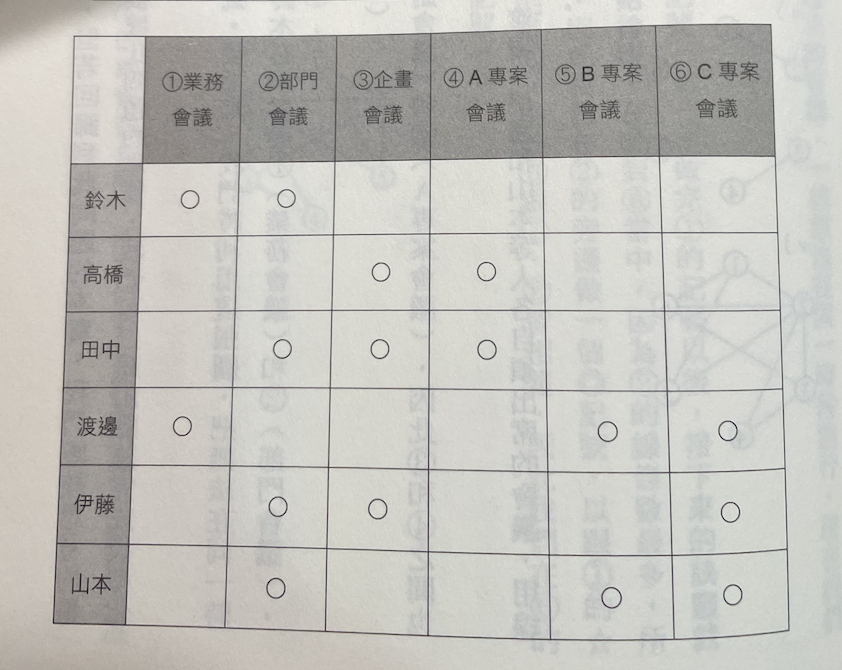
• 問題的本質：哪些會議不能在同一時段進行
• 分析流程
  1. 把 6 種會議變成點 (i)
  2. 將每個人需要參加的會議用線連起來 (ii, iii, iv) → 所有被連接的會議都無法在同一時段進行
  3. 從線條數較多 (受到限制較多) 的會議開始檢查，若遇到有線條相連的會議，就標記不同記號 (v, vi, vii)
     1. 3 雖然和 2 & 6 相連，但和 1 不相連，所以和 1 一樣打星號
     2. 4 和 6 沒有相連，打上一樣的記號
  4. 最後將記號相同的會議排在同一個時段。

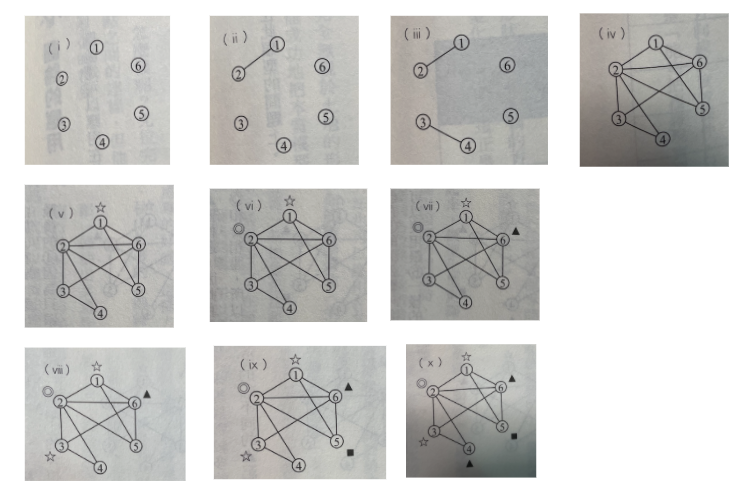
最後產生的會議群組：

• ☆ (1)業務會議 & （3）企劃會議
• ▲（4) A 專案會議 & （6）C 專案會議
• ◎（2）部門會議
• ■（5）B 專案會議

心得

今天⋯⋯當我翻到下一頁看到「圖論」這兩個字的時候，我覺得我的心靈沒有 ready 要加入新的關鍵字，剎那間有種想收工的衝動 XDD

不過因為跳過有點可恥，只好硬著頭皮看一下。然後作者又寫得實在太深入淺出，內心的獨白有點像是：「（經過一番努力後），我覺得自己好像理解了他舉的例子，但我這樣自以為看懂了，這樣真的可以嗎，話說回來，我到底看了啥小啊啊啊啊」

啊，這就是文組生的恐懼嗎？

總之，今天覺得好累啊。