昨天介紹完支持向量機(Support Vector Machines)和SMO算法,今天就要來實戰這個方法,當然因為之前有說要用二維圖去做示範,所以先用matplotlib建立兩個維度的散點圖,程式如下:

import matplotlib.pyplot as plt
import numpy as np
#label1資料 第3維為類別
label1_data=np.array([[75,-15,1],[81,12,1],[71,-9,1],[86,20,1],[40,-20,1],[81,6,1],[84,-2,1],[81,15,1],[78,4,1],[74,-1,1]])
x_label1=[label1_data[i][0] for i in range(len(label1_data))]
y_label1=[label1_data[i][1] for i in range(len(label1_data))]

#label2資料 第3維為類別
label2_data=np.array([[35,19,-1],[30,25,-1],[23,2,-1],[36,17,-1],[3,-8,-1],[31,2,-1],[21,-7,-1],[8,-27,-1],[16,-12,-1],[59,20,-1]])
x_label2=[label2_data[i][0] for i in range(len(label2_data))]
y_label2=[label2_data[i][1] for i in range(len(label2_data))]

plt.scatter(x_label1,y_label1)   
plt.scatter(x_label2,y_label2) 
plt.show() 

如圖: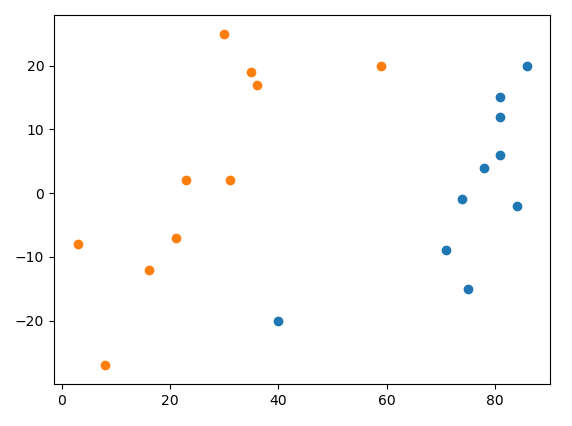

好,接下來,依照SVM公式: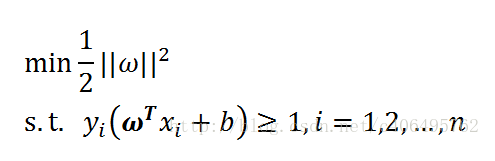



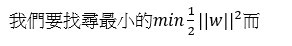
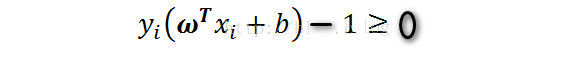
這邊我們在找最佳解問題,採用拉格朗日乘數法: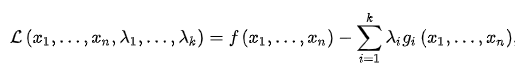


所以就會變成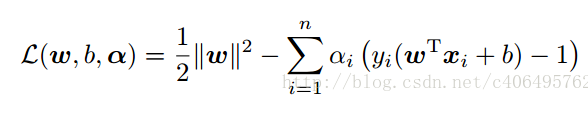

所以我們要求這個極值(對係數做偏導)

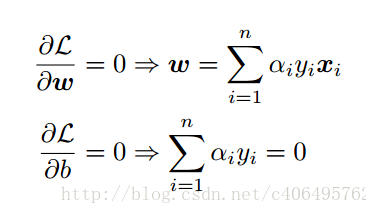
而把上述當成條件並帶回: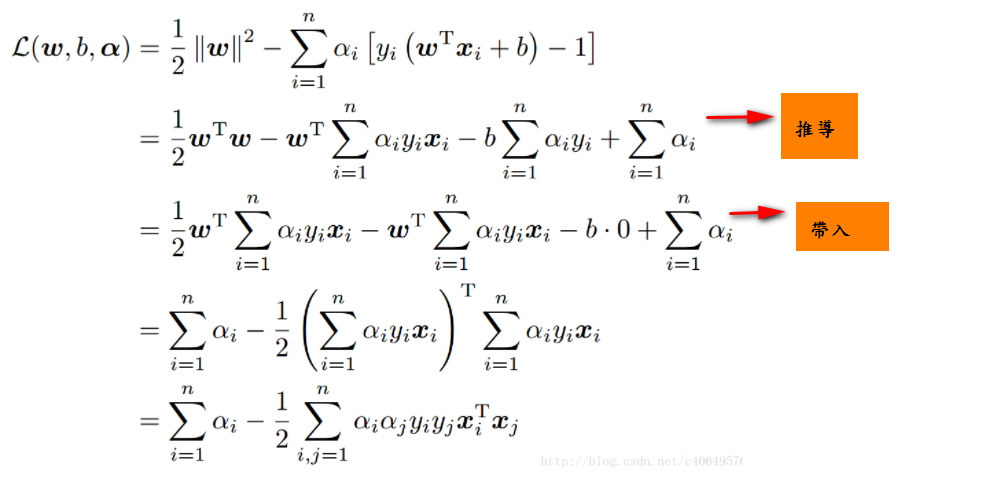

最後要再求: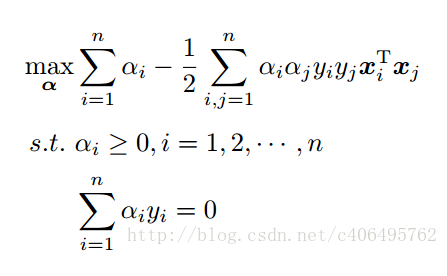

然後現在把SMO算法帶入(為了求a(就可以求到w)和b)
第一步:計算誤差:
因為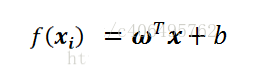

而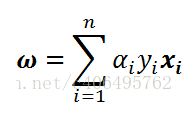

所以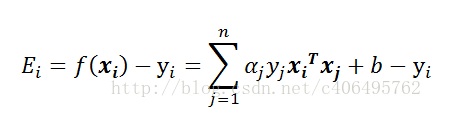

起始我們會設定a_j為0,而b也設定為0; y_i為真實類別
另外x_i為資料特徵,但x_i矩陣會長這樣

但是numpy格式資料

所以有轉置地方會剛好反過來,程式如下:

#合併資料
full_label_data=np.vstack((label1_data,label2_data))
#取出x特徵
full_label_data_x=np.mat(full_label_data[:,[0,1]])
#取出y特徵
y=np.array([full_label_data[i][2] for i in range(len(full_label_data))])
#初始a,b
a=np.zeros((1,20))
b=0

#第一步:計算誤差Ei
for i in range(len(full_label_data)):
	fXi = float(np.multiply(a,y)*(full_label_data_x*full_label_data_x[i,:].T)) + b
	print("第",i+1,"筆fXi:",fXi)
	Ei = fXi - float(y[i])
	print("第",i+1,"筆Ei:",Ei)

結果如下:

第 1 筆fXi: 0.0
第 1 筆Ei: -1.0
第 2 筆fXi: 0.0
第 2 筆Ei: -1.0
第 3 筆fXi: 0.0
第 3 筆Ei: -1.0
第 4 筆fXi: 0.0
第 4 筆Ei: -1.0
第 5 筆fXi: 0.0
第 5 筆Ei: -1.0
第 6 筆fXi: 0.0
第 6 筆Ei: -1.0
第 7 筆fXi: 0.0
第 7 筆Ei: -1.0
第 8 筆fXi: 0.0
第 8 筆Ei: -1.0
第 9 筆fXi: 0.0
第 9 筆Ei: -1.0
第 10 筆fXi: 0.0
第 10 筆Ei: -1.0
第 11 筆fXi: 0.0
第 11 筆Ei: 1.0
第 12 筆fXi: 0.0
第 12 筆Ei: 1.0
第 13 筆fXi: 0.0
第 13 筆Ei: 1.0
第 14 筆fXi: 0.0
第 14 筆Ei: 1.0
第 15 筆fXi: 0.0
第 15 筆Ei: 1.0
第 16 筆fXi: 0.0
第 16 筆Ei: 1.0
第 17 筆fXi: 0.0
第 17 筆Ei: 1.0
第 18 筆fXi: 0.0
第 18 筆Ei: 1.0
第 19 筆fXi: 0.0
第 19 筆Ei: 1.0
第 20 筆fXi: 0.0
第 20 筆Ei: 1.0 

好,今天支持SMO算法第一步算是完成了,明天就開始寫第二部分

男孩發現胸口聲音消失,取而代之是一種恐懼和憤怒感覺聰他胸口發出,男孩不清楚發生了,甚麼事,他只想趕快離開這間小木屋,離開這,於是他衝了出來,並朝著森林深處狂奔,只是他沒有發現到,他的口袋裡的紙條掉落在小木屋內,在男孩走後,紙條突然燒了起來,偶後,從灰燼裡出現了一隻狐狸,只不過他一動也不動,像是在等待誰的到來
		--|我所做的一切都是為了你|--  MS.CM