昨天介紹完SMO算法第一步,今天就要來寫這個方法第二步,
而第2步步驟:選取兩個點,並計算上下界H和L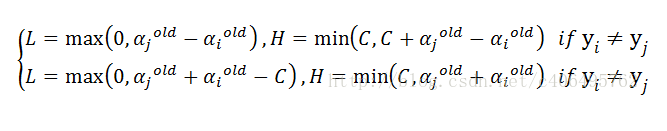

C是自定義容許值,之前有說: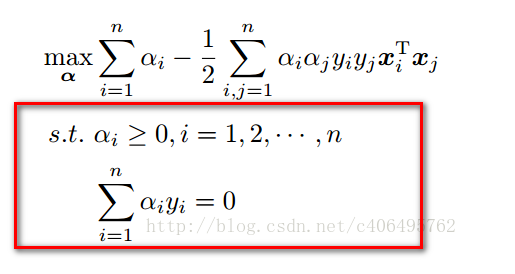

現在幫他加一個上限C,所以就會變成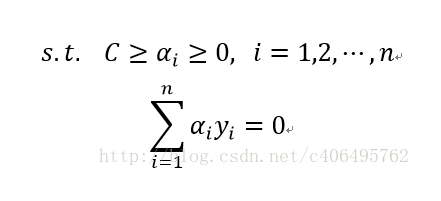

(免得ai 發散)
並且依照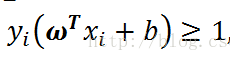

和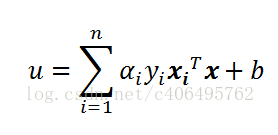

可以得知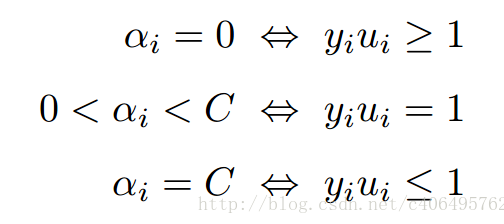

另外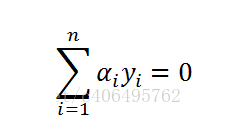

所以

也就是在每次跌代都要保持這等式,這時上下界為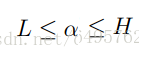

所以以二維為例,可能結果為: (y要是1或-1)-->類別不一樣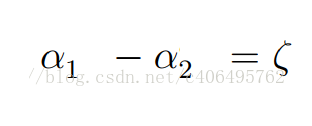

(令a1=c(最大值))
最大值H: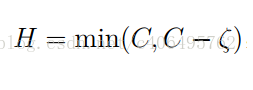

(令a1=0(最小值))
最小值L: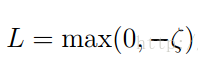

和類別一樣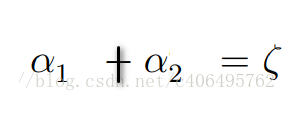

所以以此類推
(令a1=0(最大值))
最大值H: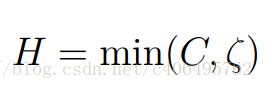

(令a1=c(最小值))
最小值L: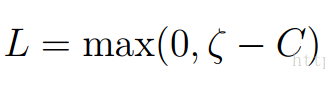

把上述分兩組,每一組各3個方程式解聯立
1.



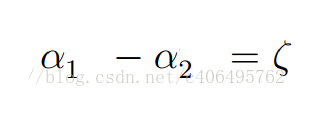
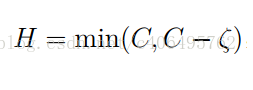
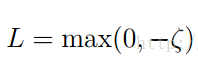
2.



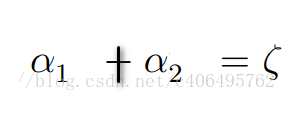
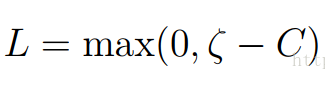
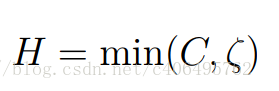
就可以得到一開始式子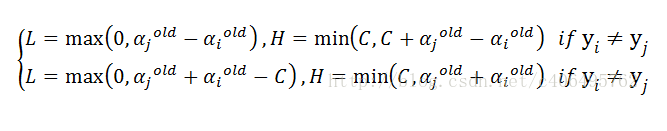

程式碼如下:
一開始先創建選擇函數:

import random
def select_J(i, m): #選擇i不等於j
    j = i                                 
    while (j == i):
        j = int(random.uniform(0, m))
    return j

之後來創建上下界,並設定c

#設定a上界C
C=0.6
#第二步:計算上下界(每個i都要做)
j=select_J(i,len(full_label_data))
#不同邊
if (y[i] != y[j]):
	L = max(0, a[0][j] - a[0][i])
	H = min(C, C + a[0][j] - a[0][i])
#同邊
else:
	L = max(0, a[0][j] + a[0][i] - C)
	H = min(C, a[0][j] + a[0][i])
print("第",i+1,"筆H:",H)
print("第",i+1,"筆L:",L)

這樣子就可以求到

第 1 筆H: 0.6
第 1 筆L: 0
第 2 筆H: 0.6
第 2 筆L: 0
第 3 筆H: 0.0
第 3 筆L: 0
第 4 筆H: 0.6
第 4 筆L: 0
第 5 筆H: 0.6
第 5 筆L: 0
第 6 筆H: 0.0
第 6 筆L: 0
第 7 筆H: 0.6
第 7 筆L: 0
第 8 筆H: 0.0
第 8 筆L: 0
第 9 筆H: 0.0
第 9 筆L: 0
第 10 筆H: 0.0
第 10 筆L: 0
第 11 筆H: 0.6
第 11 筆L: 0
第 12 筆H: 0.0
第 12 筆L: 0
第 13 筆H: 0.6
第 13 筆L: 0
第 14 筆H: 0.0
第 14 筆L: 0
第 15 筆H: 0.0
第 15 筆L: 0
第 16 筆H: 0.0
第 16 筆L: 0
第 17 筆H: 0.0
第 17 筆L: 0
第 18 筆H: 0.0
第 18 筆L: 0
第 19 筆H: 0.0
第 19 筆L: 0
第 20 筆H: 0.0

當然這邊是沒有更新a,所以L和H會是0(之後會更新),另外如果L等於H這樣就可以確定a

好,今天支持SMO算法第二步算是完成了,明天就開始寫第三部分

視角轉回男人身上,男人用輕快的步伐來到森林入口,他看到了入口處的告示牌,只不過上面文字似乎和男孩看到的不太一樣,上面寫著:請勿進入, 男人笑了笑,隨即用手放在告示牌,只見告示牌突然燒了起來,並發出淒慘的尖叫聲,然後隨即消失在空氣中, 男人隨即踏著輕快步伐,繼續往森林裡走
		--|我遵守了約定,只是更改了內容,甚麼都不剩|--  CS.MM