前言：介紹完了二元樹的建立和走訪方式，緊接著要來介紹其他基本應用，一樣用上一篇的程式碼進行修改

可以先把之前的程式碼改成T指針類型，後續的操作會比較方便，更改方式如圖：
注意!!! BiTree()原本T的地方改成root，避免命名重複導致程式錯誤(一開始命名的不好是我的疏忽˃ʍ˂)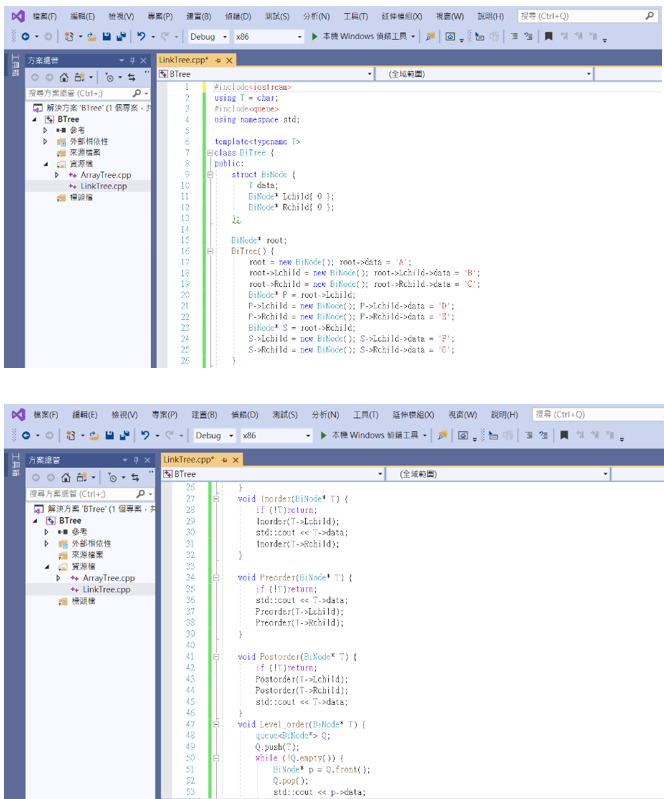


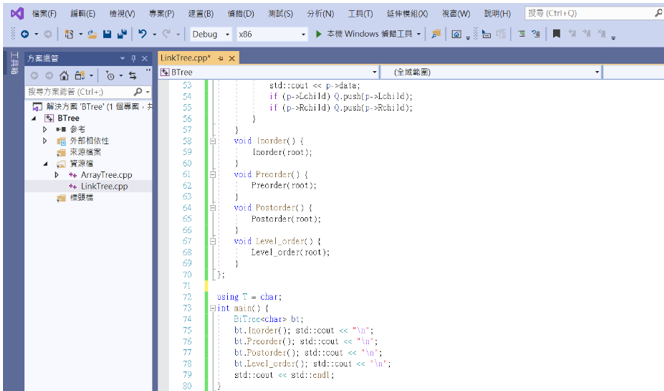
接著就可以開始實作囉

1.求二元樹的深度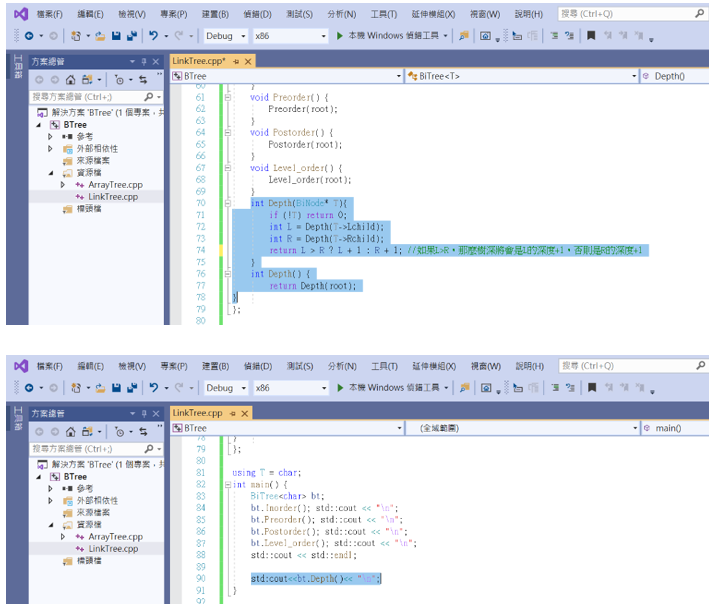

可以看到樹的深度如預期的一樣為3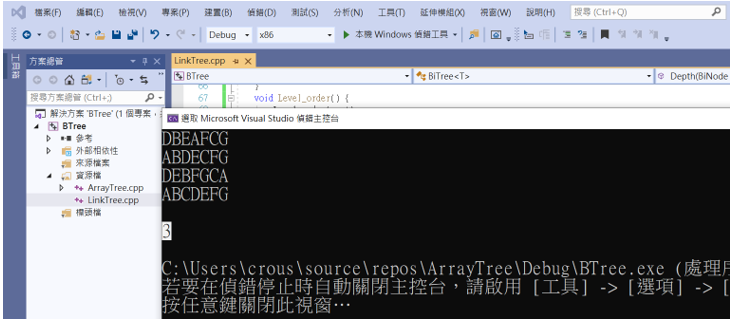

2.計算樹的葉節點數目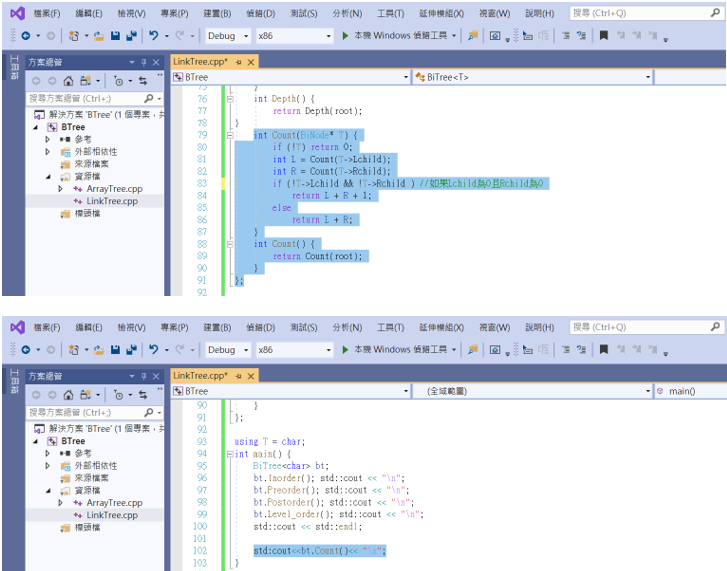

可以看到葉節點的各數為4(DEFG)。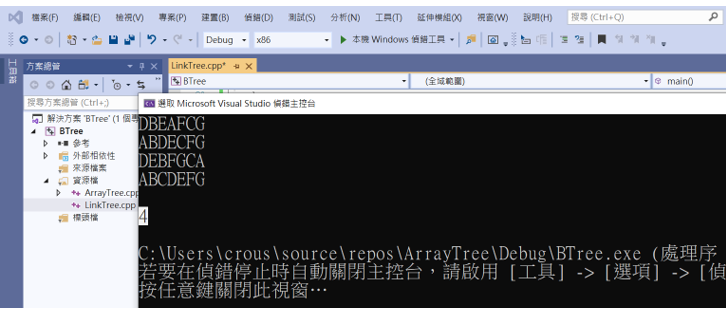

也可以把判斷式改成if (!T->Lchild && !T->Rchild || !T->Lchild && T->Rchild)則可以檢查多餘的節點，來判斷是否為嚴格二元樹。

3.利用空節點標記符號(#)來建立二元樹
相信很多人不懂這題的意思，其實是在走訪節點的下一個節點不存在時(沒有子節點)，輸出一個#。

先修改之前的前序走訪作為範例。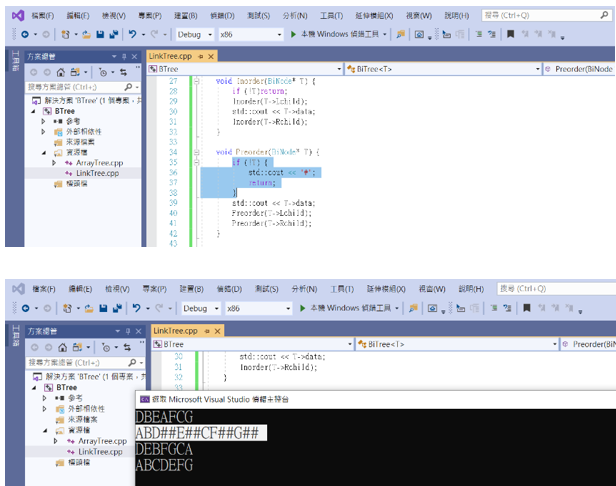

這樣做的意義在哪呢？
這樣做是方便還原二元樹的樣貌，如果沒有這些符號，二元樹會有多種可能，不只是人，連電腦也無法判斷出這個二元樹原本的樣貌，來實際畫畫看就知道了。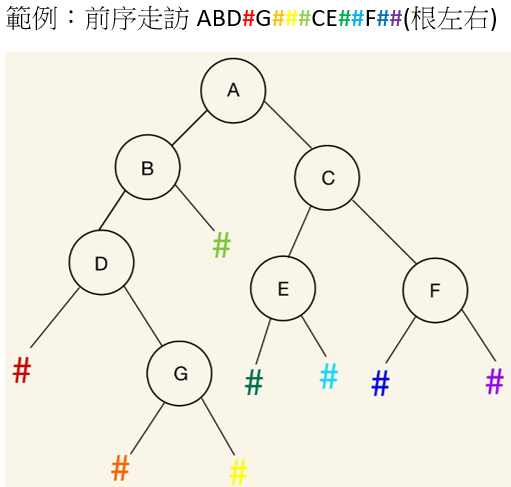

左節點優先權大於右節點，所以都是先從左邊開始畫

接著我們現在要做的就是輸入一串帶有空節點符號的前序序列，來讓電腦建立二元樹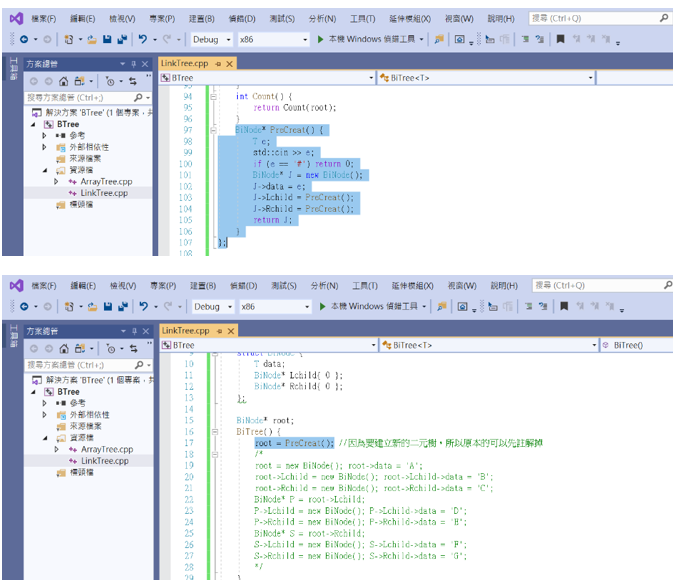

接著輸入前序串列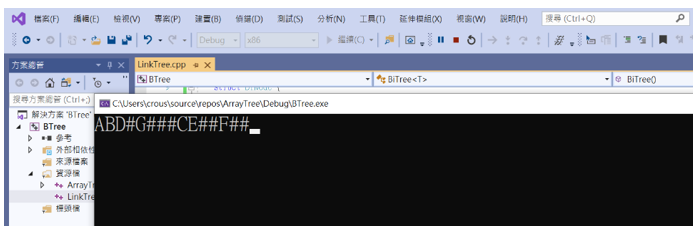

如果有跑出結果就代表建立成功，順便檢查和第三行是不是一樣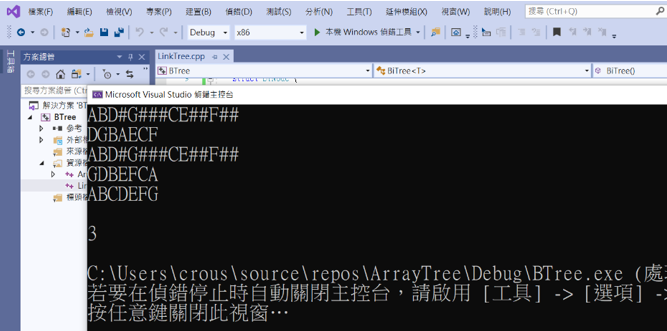

這種方法也可以用在另外三種走訪方式，有興趣的人可以自己操作看看

今日小結：今天講了一些常見但實用的小技巧，尤其是第三個利用空節點符號轉回二元樹的方法，算是相當重要的必備技能，其實樹還有非常多衍生跟應用，只不過也是會花太多篇幅，有機會再向大家介紹，樹的部分先告一段落，明天也將要進入新的環節。

#include<iostream>
using T = char;
#include<queue>
using namespace std;

template<typename T>
class BiTree {
public:
	struct BiNode {
		T data;
		BiNode* Lchild{ 0 };
		BiNode* Rchild{ 0 };
	};

	BiNode* root;
	BiTree() {
		root = PreCreat(); //因為要建立新的二元樹，所以原本的可以先註解掉
		/*
		root = new BiNode(); root->data = 'A';
		root->Lchild = new BiNode(); root->Lchild->data = 'B';
		root->Rchild = new BiNode(); root->Rchild->data = 'C';
		BiNode* P = root->Lchild;
		P->Lchild = new BiNode(); P->Lchild->data = 'D';
		P->Rchild = new BiNode(); P->Rchild->data = 'E';
		BiNode* S = root->Rchild;
		S->Lchild = new BiNode(); S->Lchild->data = 'F';
		S->Rchild = new BiNode(); S->Rchild->data = 'G';
		*/
	}
	void Inorder(BiNode* T) {
		if (!T)return;
		Inorder(T->Lchild);
		std::cout << T->data << " ";
		Inorder(T->Rchild);
	}

	void Preorder(BiNode* T) {
		if (!T) {
			std::cout << "#" << " ";
			return;
		} 
		std::cout << T->data;
		Preorder(T->Lchild);
		Preorder(T->Rchild);
	}

	void Postorder(BiNode* T) {
		if (!T)return;
		Postorder(T->Lchild);
		Postorder(T->Rchild);
		std::cout << T->data << " ";
	}
	void Level_order(BiNode* T) {
		queue<BiNode*> Q;
		Q.push(T);
		while (!Q.empty()) {
			BiNode* p = Q.front();
			Q.pop();
			std::cout << p->data << " ";
			if (p->Lchild) Q.push(p->Lchild);
			if (p->Rchild) Q.push(p->Rchild);
		}
	}
	void Inorder() {
		Inorder(root);
	}
	void Preorder() {
		Preorder(root);
	}
	void Postorder() {
		Postorder(root);
	}
	void Level_order() {
		Level_order(root);
	}
	int Depth(BiNode* T){
		if (!T) return 0;
		int L = Depth(T->Lchild);
		int R = Depth(T->Rchild);
		return L > R ? L + 1 : R + 1; //如果L>R，那麼樹深將會是L的深度+1，否則是R的深度+1
	}
	int Depth() {
		return Depth(root);
}
	int Count(BiNode* T) {
		if (!T) return 0;
		int L = Count(T->Lchild);
		int R = Count(T->Rchild);
		if (!T->Lchild && !T->Rchild) //如果Lchild不為0且Rchild不為0
			return L + R + 1;
		else
			return L + R;
	}
	int Count() {
		return Count(root);
	}
	BiNode* PreCreat() {
		T e;
		std::cin >> e;
		if (e == '#') return 0;
		BiNode* J = new BiNode();
		J->data = e;
		J->Lchild = PreCreat();
		J->Rchild = PreCreat();
		return J;
	}
};

using T = char;
int main() {
	BiTree<char> bt;
	bt.Inorder(); std::cout << "\n";
	bt.Preorder(); std::cout << "\n";
	bt.Postorder(); std::cout << "\n";
	bt.Level_order(); std::cout << "\n";
	std::cout << std::endl;

	std:cout<<bt.Count()<< "\n";
}