前言：在第11天的時候我們有討論到佇列，今天就是來把之前的坑給補上的，先前沒有提到的就是等等要介紹的「優先佇列」，因為優先佇列和堆積有些關係，所以放在這篇一起講。

優先佇列(Priority Queue)：

稍微幫大家複習一下，如果忘記的可以去看看之前的文章。

普通的佇列是一種先進先出的數據結構，元素在佇列尾端被加入，而刪除和查找都是從佇列前端執行。
而在優先佇列中，元素被賦予優先級，當訪問到元素時，具有最高優先級的元素會最先被刪除，就像是VIP在能有優先進場的資格一樣，而優先佇列通常都會利用「堆積」來完成。

程式實作：用VS2019內部的佇列方法簡單實作一下，之後會再完整的練習。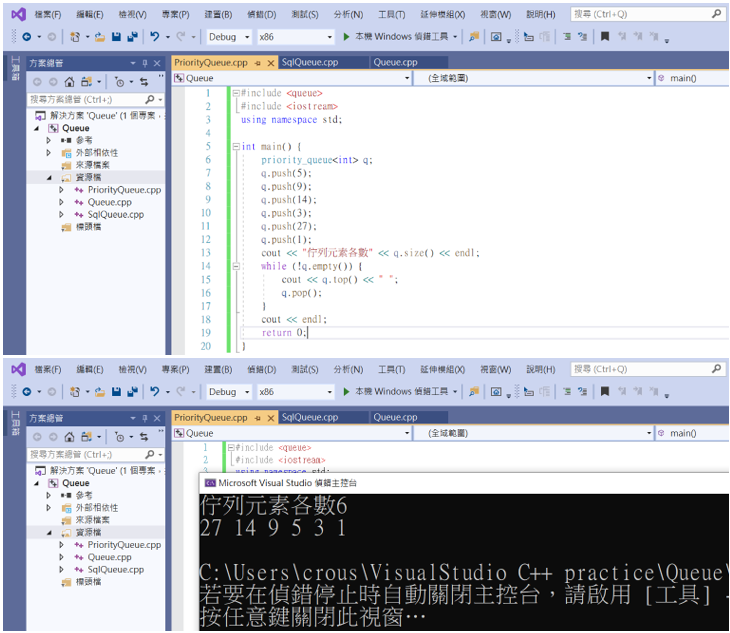

優先佇列的五種實現方式：

1. 無序數組
2. 有序數組
3. 鏈接串列(有序或無序都可)
4. 二元排序樹或平衡二元樹(非本次重點暫不討論)
5. 堆積(最有效率)

快速介紹完了優先堆積，接著就要進入今天的重頭戲。

堆積(Heap)：

堆積有很多種類，今天就只介紹最基本的最大堆積(Max-Heap)和最小堆積(Min-Heap)。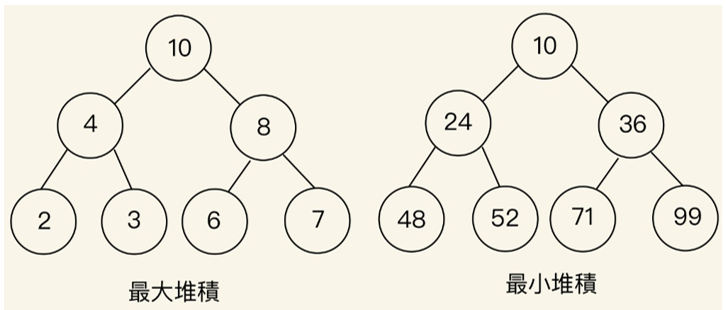

是不是覺得非常眼熟？堆積其實是完整二元樹的一種，只要滿足如上圖的條件( 最大或最小的元素在樹跟，其餘元素由小到大或由大到小排列 )，完整二元樹就可以稱作堆積。

最大堆積：樹跟為最大值，所有節點值均不小於它的子節點的值。
最小堆積：樹跟為最小值，所有節點值均不大於它的子節點的值。

堆積的特性也很適合使用在排序，稱為堆積排序法，等之後進入演算法的環節在充分介紹。

堆積操作概念：
•由上而下，從樹根開始與其子節點開始比較，若前者較大則不用交換，反之，則要交換；以符合父節點大於子節點的規則。
•由下而上，從樹葉開始與其父節點開始比較，若後者較大則不用交換，反之，則要交換；以符合父節點大於子節點規則。

這類方法子節點(父節點)先比，找出最大者再與父節點(子節點)交換，這樣就只要交換一次就行，所以如果有交換節點的情況發生，這類方法是最推薦的。

本日小結：優先佇列和堆積的概念說明就先到這裡結束，明天要來實際創建堆積，並嘗試時做向上和向下的調整，如果可以希望還能講解一下AMC程式競賽的題目。今天稍微輕鬆一點，明天還要繼續努力(*•̀ㅂ•́)و

#include <queue>
#include <iostream>
using namespace std;

int main() {
	priority_queue<int> q;
	q.push(5);
	q.push(9);
	q.push(14);
	q.push(3);
	q.push(27);
	q.push(1);
	cout << "佇列元素各數" << q.size() << endl;
	while (!q.empty()) {
		cout << q.top() << " ";
		q.pop();
	}
	cout << endl;
	return 0;
}