前言

什麼是貝茲曲線？它能創造一連串平滑的曲線，被應用在PS和AI中的鋼筆、以及常見的CSS Animation，換句話說，你學會了貝茲曲線，就大概懂一半網頁動畫了，它厲害的地方在於，用一個很簡單並直覺的方式來設定動畫，加上其可視化的特性，在上述例子中都能很輕鬆的運用。

像是在這個網站用滑鼠拉動控制桿後，就可以輕易地拿到參數，把它複製到CSS Animation的設定中，就能輕鬆產生動畫。

參考資料

起初是沒打算拿貝茲曲線來作文章的，CSS已經有框架可以用了，為什麼我們還要用JS從底層實作一遍呢？這個論點大致上沒錯，不過，昨晚睡前我不經意看到了這部影片：The Beauty of Bézier Curves

這部影片，是我目前為止看過講的最簡單易懂的貝茲曲線，包含很完整的綱要和學習步驟，當然，裡面還是包含了一些數學，但重要的是，它有談到如何透過簡化的公式實現美麗的貝茲曲線，並且，我們的眼光可以不侷限於CSS的框架，透過多條貝茲曲線的連接，可以輕鬆實現昨天所說的「尋路問題」，並打破原先的隨機性和不可預測性。

雖然是推薦大家看原版英文的影片（有CC字幕），享受質感，不過還是提供大家英文苦手的選擇：bilibibli的翻譯版本

三次方貝茲曲線 Cubic Bezier Curves

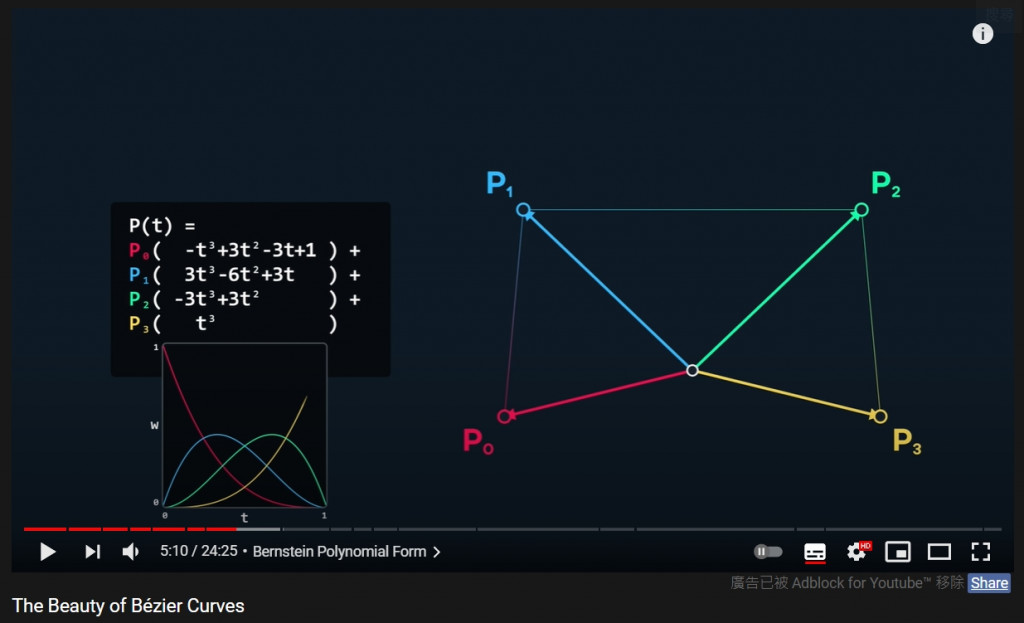
這邊我們設計一個向量物件，來描述貝茲曲線的四個基本點，名稱和教學中採用一致的(p0, p1, p2 ,p3)

function vector(x, y){
    this.x = x;
    this.y = y;
}
function bezierCurves(x0, y0, x1, y1, x2, y2, x3, y3){
    this.p0 = new vector(x0, y0);
    this.p1 = new vector(x1, y1);
    this.p2 = new vector(x2, y2);
    this.p3 = new vector(x3, y3);
    this.timestamp = Date.now();
    this.lifeTime = 2;
}

然後把路徑的公式描繪出來，為了能清楚呈現多項式中的次方項，採用Math.pow的寫法，而不是t x t x t，一樣是在原型上添加方法

bezierCurves.prototype.Path = function(){
    let P = function(a, b){
        return Math.pow(a, b);
    }
    return {'x': x0 * (-1 * P(t ,3) + 3 * P(t ,2) - 3 * P(t ,1) + 1 )
                +x1 * ( 3 * P(t ,3) - 6 * P(t ,2) + 3 * P(t ,1))
                +x2 * (-3 * P(t ,3) + 3 * P(t ,2))
                +x3 * ( 1 * P(t ,3)),
            'y': y0 * (-1 * P(t ,3) + 3 * P(t ,2) - 3 * P(t ,1) + 1 )
                +y1 * ( 3 * P(t ,3) - 6 * P(t ,2) + 3 * P(t ,1))
                +y2 * (-3 * P(t ,3) + 3 * P(t ,2))
                +y3 * ( 1 * P(t ,3))}
}

然後我們試著讓一條新的貝茲曲線接上舊的，一樣是設計animeList跑迴圈時所呼叫的NextFrame方法：

bezierCurves.prototype.NextFrame = function(){
    // 計算下一偵的位置(0~1)
    let dT = (Date.now() - this.timestamp) / 1000 / this.lifeTime;
    if(dT <= 1){
        let point = bezierCurves.prototype.Path(dT);
        context.save();
        context.translate(pointX, pointY);
        context.drawImage(mouseImg, -mouseImg.width/2, -mouseImg.height/2);
        context.restore();
    }
    else{
        // 製作一個閉環
        let newObject = new bezierCurves(this.p3.x, this.p3.y,
                                         this.p3.x * 2 - this.p2.x,
                                         this.p3.y * 2 - this.p2.y,
                                         this.p0.x * 2 - this.p1.x,
                                         this.p0.y * 2 - this.p1.y,
                                         this.p0.x, this.p0.y);
        let index = animeList.indexOf(this);
        delete animeList[index];
        animeList[index] = newObject;
    }
}

有點快睡著了，打code打到度估，今天就先這樣了不好意思><，這幾天有空再回來補demo吧!

其他：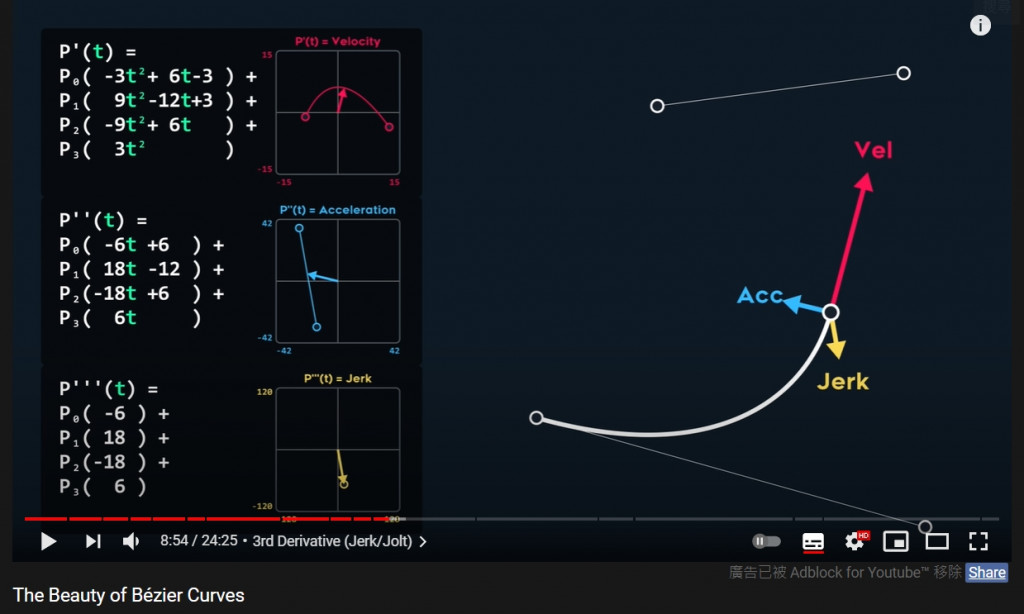

bezierCurves.prototype.Velocity = function(){
    let P = function(a, b){
        return Math.pow(a, b);
    }
    return {'x': x0 * (-3 * P(t ,2) +  6 * P(t ,1) - 3 )
                +x1 * ( 9 * P(t ,2) - 12 * P(t ,1) + 3 )
                +x2 * (-9 * P(t ,2) +  6 * P(t ,1))
                +x3 * ( 3 * P(t ,2)),
            'y': y0 * (-3 * P(t ,2) +  6 * P(t ,1) - 3 )
                +y1 * ( 9 * P(t ,2) - 12 * P(t ,1) + 3 )
                +y2 * (-9 * P(t ,2) +  6 * P(t ,1))
                +y3 * ( 3 * P(t ,2))}
}
bezierCurves.prototype.Acceleration = function(){
    let P = function(a, b){
        return Math.pow(a, b);
    }
    return {'x': x0 * ( -6 * P(t ,1) +  6 )
                +x1 * ( 18 * P(t ,1) - 12 )
                +x2 * (-18 * P(t ,1) +  6 )
                +x3 * (  6 * P(t ,1)),
            'y': y0 * ( -6 * P(t ,1) +  6 )
                +y1 * ( 18 * P(t ,1) - 12 )
                +y2 * (-18 * P(t ,1) +  6 )
                +y3 * (  6 * P(t ,1))}
}
bezierCurves.prototype.Jerk = function(){
    let P = function(a, b){
        return Math.pow(a, b);
    }
    return {'x': x0 * ( -6 )
                +x1 * ( 18 )
                +x2 * (-18 )
                +x3 * (  6 ),
            'y': y0 * ( -6 )
                +y1 * ( 18 )
                +y2 * (-18 )
                +y3 * (  6 )}
}