堆積排序法(Heap Sort)原理是利用「堆積」的資料結構為基礎來完成排序。

堆積的介紹可以參考此篇。

操作流程(最大堆積為例):

1. 將陣列轉換最大堆積(Max Heap)
2. 將Root與最後一個節點交換
3. 將最後一個節點移除
4. 將剩餘為排序完的節點重複1~3步驟，直到所有節點被移除，即完成排序。

下面利用30 20 15 1 10 5由小到大排序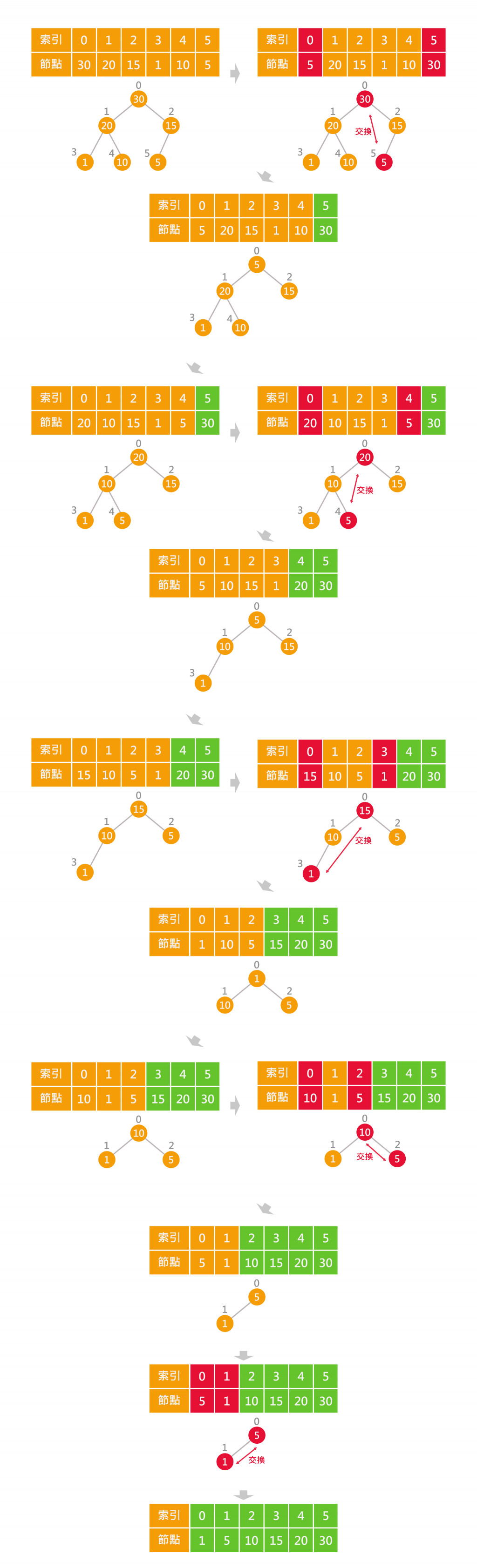

時間複雜度 = 建立堆積 + 移除堆積

建立堆積: Ο(n)
移除堆積: n-1次，(n-1) X Ο(log n) = Ο(n log n)

Ο(n) + Ο(n log n) = Ο(n log n)

平均時間複雜度為: O(n log n)

JavaScript

let data = [30,20,15,1,10,5];

function maxHeapify(arr, n, i){
  let largest = i;
  let l = 2 * i + 1;
  let r = 2 * i + 2;
  
  // 若左子樹大於根結點時
  if (l < n && arr[l] > arr[largest]) {
        largest = l; 
  }
  
  // 若右子樹大於根結點時
  if (r < n && arr[r] > arr[largest]) {
      largest = r; 
  }
  
  // 根節點不是最大值時
  if (largest != i) { 
    [arr[i],arr[largest]] = [arr[largest],arr[i]]
    // 子樹堆積化遞迴 
    maxHeapify(arr, n, largest); 
  } 
}

 function heapSort(arr) { 
    let n = arr.length
    // 建立最大堆積化
    for (let i = parseInt(n / 2 - 1); i >= 0; i--) {
        maxHeapify(arr, n, i); 
    }
  
    //逐一從最後節點拿出
     for (let i = n - 1; i >= 0; i--) { 
        // 根節點與最後節點交換位置
        [arr[0],arr[i]] = [arr[i],arr[0]]
        maxHeapify(arr, i, 0); 
     } 
 }
 
 heapSort(data);
 console.log(data);//[1, 5, 10, 15, 20, 30]

Python

#Heap Sort

def maxHeapify(arr, n, i):
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2
  
    if l < n and arr[i] < arr[l]:
        largest = l
  
    if r < n and arr[largest] < arr[r]:
        largest = r
  
    if largest != i:
        arr[i],arr[largest] = arr[largest],arr[i]
        maxHeapify(arr, n, largest)
  
def heapSort(arr):
    n = len(arr)

    for i in range(n // 2 - 1, -1, -1):
        maxHeapify(arr, n, i)
  
    for i in range(n-1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        maxHeapify(arr, i, 0)

data = [30,20,15,1,10,5]
heapSort(data)
print(data)
#1,5,10,15,20,30