上回提到電腦最基本的原理就是由許多開關組成的,今天我們就用這些開關來組合出一個「加法器」,來體會一下這個概念。
加法器顧名思義就是用來處理計算機的加法。首先讓我們回想一下我們是如何將兩個二進制數字 X、Y 相加的?我們會由個位數開始,把 X 和 Y 的個位數加起來,得到的結果如果有進位的話會保留給十位數,剩下沒有進位的部分就放在結果的個位數。進到十位數時,除了原本的 X 和 Y 的十位數相加之外,還要再加上剛剛個位數進位的部分,而最後也會像個位數相加時一樣,得到一個十位數的相加結果,和十位數的進位結果。這樣一直往更高位數運算,就能得到相加結果了。所以我們的方向是先做出一個可以處理一個位數相加的小元件,再將它們串連起來,就能得到多個位數相加的結果。
底下來簡單體驗一下:
首先做出一個「半加器」:輸入有 X 和 Y,各是 0 或 1,分別表示要相加的兩個只有一位的數;輸出有 S 表示該位數的和,C 表示進位,也分別是 0 或 1。將結果畫成真值表:
| X | Y | S | C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
根據真值表,我們會發現 S 的結果其實就是 X OR Y,C 的結果就是 X AND Y,這樣一來就能畫出半加器的電路圖: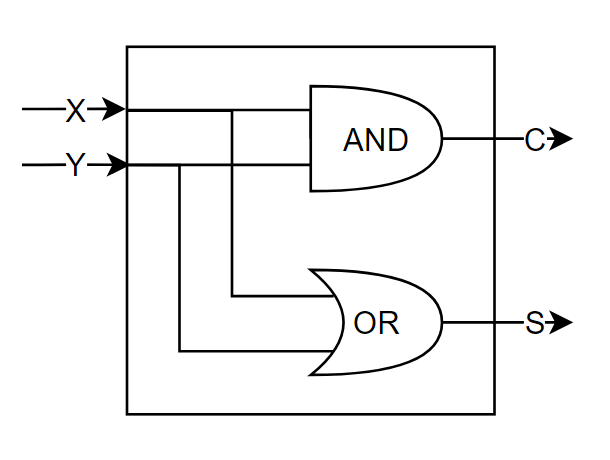
但根據第一段的描述,一個位數完整的相加,除了 X、Y 兩個輸入之外,還要考慮來自低位數的進位,所以我們要再設計一個全加器,新增輸入值 Cin,而要進位的輸出值改叫做 Cout。這樣可以畫出一個更大的真值表:
| X | Y | Cin | S | C |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
透過一些布林代數的簡化(這邊細節就不推導了),加上利用剛剛畫出的半加器,我們又可以再畫出一個全加器的電路圖(這裡省略)。
有了可以計算一個位數(bit)的全加器,最後再將多個全加器串連起來,就可以得到多個位數相加的結果,例如我們可以用 4 個全加器串聯出一個可以做 4 bit 數字相加的加法器。
以上是電腦會使用到的一個基礎電路的介紹,細節沒有說得很清楚,不過大家應該能體會到之前講說「電腦就是許多小開關所組成的」這句話的意思吧。實際上除了加法器以外,還有許多不同的元件,他們的電路都是用相似的方法設計而成,所以說布林代數和二進位可以說是現代電腦的理論基礎。
目前為止講的都是偏向理論,但是實際上到底怎麼把一堆開關塞到電腦裡面的呢?下回我們來談談複雜的電路圖是如何變成我們實際可以使用的電腦的。
