圖片來源

「矩陣」是最強大的空間扭曲招數。

它比其他「空間忍數」：位移、縮放、旋轉這三個加起來都強！因為他一次就可以作掉這三個，而且解決了這三個的致命缺點——順序！它堪稱像是火影忍者扭曲空間一樣強大！

現在，讓我們習得扭曲空間吧！

回顧上篇，介紹了3D場景中每一個物件的上下層樹狀結構關係。

亦即：child的空間是相對於parent的，parent的空間又是相對於它的parent。

這種結構，位移、縮放、旋轉（下面總稱「形變」）相當麻煩，那不要有樹狀結構不就好了？就把它展開來，大家都在世界空間裡面。

這是很好的方法，但如果你的形變一複雜，你仍要面對順序問題，形變的順序會影響結果。

順序為什麼有差？

我們先看看你隔壁的同事怎麼面對這個問題：

在Figma看這個問題：

他是一個設計師，有一天PM叫他修改設計稿，說要「兩按鈕距離變成30px，然後畫布等比例放大一倍」。

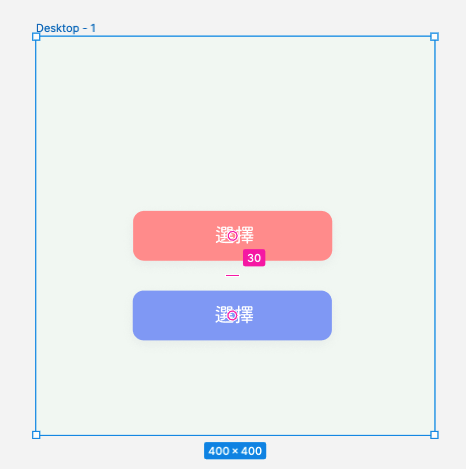
你同事就往下30px，然後等比例放大一倍。

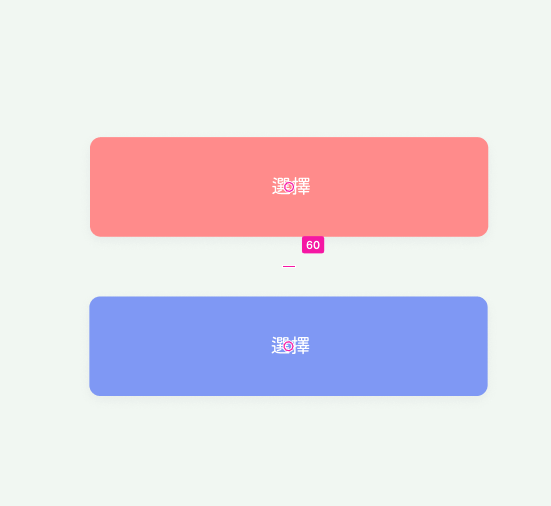
PM後來問他：「不是往下30px嗎？怎麼往下60px了？」

同事說：「你不是要變成60px，『然後』放大一倍嗎？」

如果PM今天前後顛倒，講「畫布等比例放大一倍，然後按鈕距離要變成60px」，那結果就會不一樣。

登楞，這才發現這個「然後」很重要。

好啦以上都是虛構我知道很瞎，只是想表達「順序有差」。你在3D場景中「先縮放再位移」，會跟「先位移再縮放」有差別。直接看Code。

在Three.js看這個問題

一樣我從上次的程式碼開始，這邊附上昨天的codePen

https://codepen.io/umas-sunavan/pen/YzLZvpM

我們把樹狀結構拿掉，變成一個只有一個方形的場景。

作法是：先把parent跟child刪掉，改成只剩下cube

// 刪掉parent跟child，換成cube
// const parent = new THREE.Mesh(geometry, material);
// const child = new THREE.Mesh(geometry, material);
const cube = new THREE.Mesh(geometry, material);

// 刪掉parent跟child
// scene.add(parent);
// scene.add(child);
scene.add(cube);

// 不旋轉了
// parent.position.x = 10
// child.position.x = 5

function animate() {
	// 不旋轉了
  // parent.rotation.y += 0.01;
	requestAnimationFrame( animate );
	renderer.render( scene, camera );
}

現在長這樣，很單純。

在Three.js看順序問題：先觀察

左圖是先位移再縮放，右圖是先縮放再位移，你會看出差別。

這是CodePen，可以點進去把18、19行互相置換

https://codepen.io/umas-sunavan/pen/JjvNYwY

由此可知，順序出現問題。

那該如何解決問題呢？

矩陣

如果沒有學過線性代數也不用慌張，我們重新溫習矩陣，我很簡單的介紹一下。

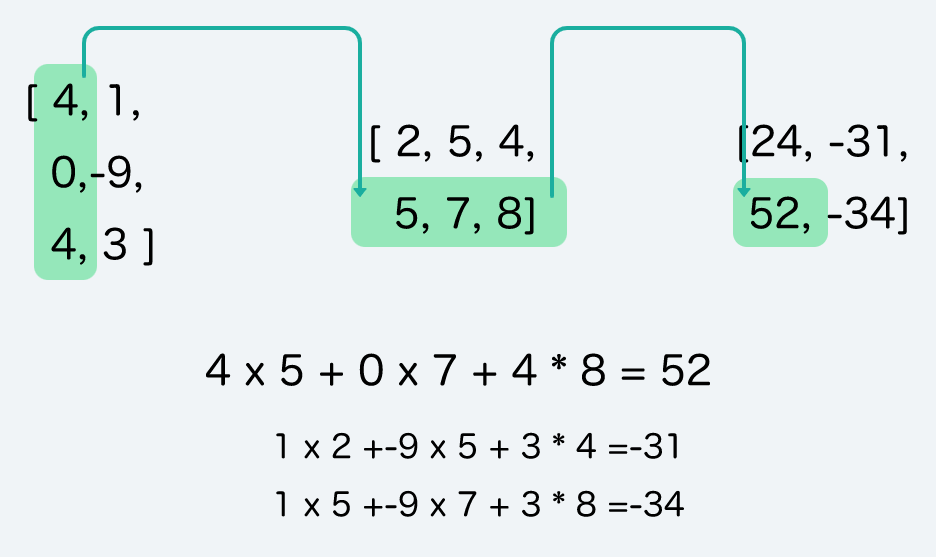
你還有印象的話，矩陣的乘法像這樣：

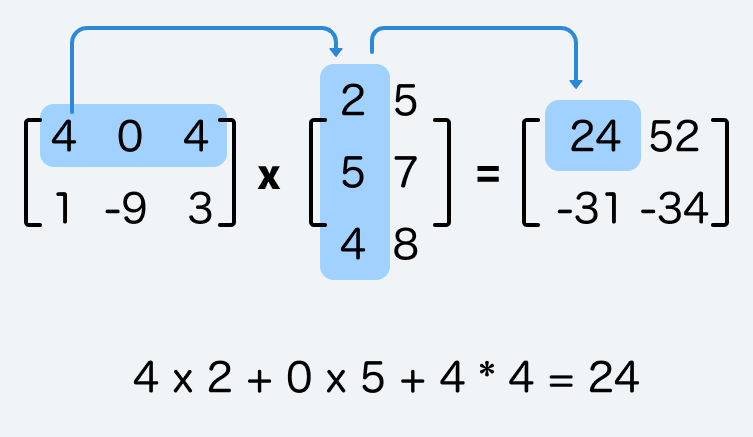
第一列的4 ，乘上了第一欄的2。那列乘上那欄，變成24

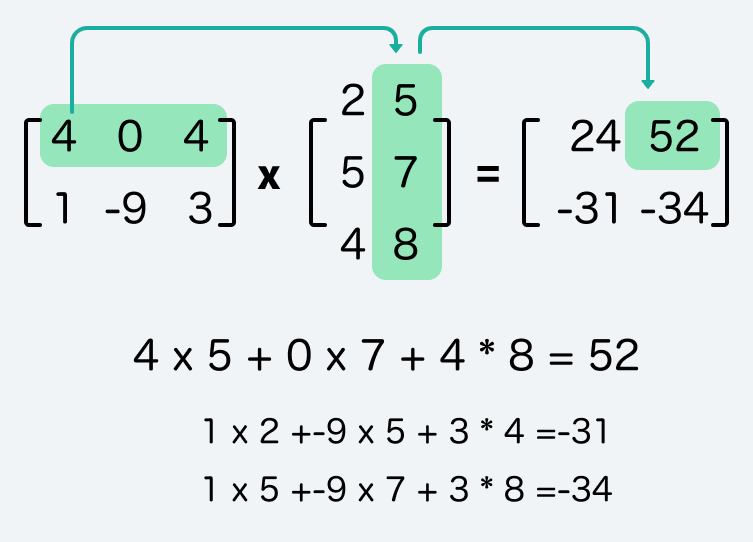
第一列的再接續乘上第二欄，得到52。

這樣應該可以喚起你高中的記憶。

矩陣：在程式語言的表示方式與數學不同

喚醒之後，我們這邊要做一點改變：在程式語言中，欄列是相反的。

為什麼？由於程式語言很難表達下面這組矩陣。

// matrix1 x matrix2 = answer
           |2 5|
|4  0 4| x |5 7| = | 24  52|
|1 -9 3|   |4 8|   |-31 -34|

畢竟寫成陣列不太方便計算。為了方便運算起見，從前的工程師就把欄改成列，列改成欄，變成用這個方式表達矩陣：

const matrix1 = [4, 1
				 0,-9
				 4, 3]

const matrix2 = [2, 5, 4
				 5, 7, 8]

const answer = [24, -31,
				52, -34]

你會發現，欄跟列顛倒了！

如果很好奇其中的原因，可以參考這邊：

https://webglfundamentals.org/webgl/lessons/webgl-matrix-vs-math.html

接下來我都改成用程式語言方式表達

矩陣：用來位移

從前從前，有一個天才，發現可以用上面那個計算方式，同時代表位移、縮放、旋轉！

他是這樣辦到的，下面以二維空間說明：

1. 有一個位置，假設(x,y)好了，要位移(tx, ty)。

   const position = [x,y]
   const translation = [tx, ty]
   

2. 為了能夠計算，這位天才幫(x,y)加上一個1，變成(x,y,1)

   const position = [x,y,1]
   

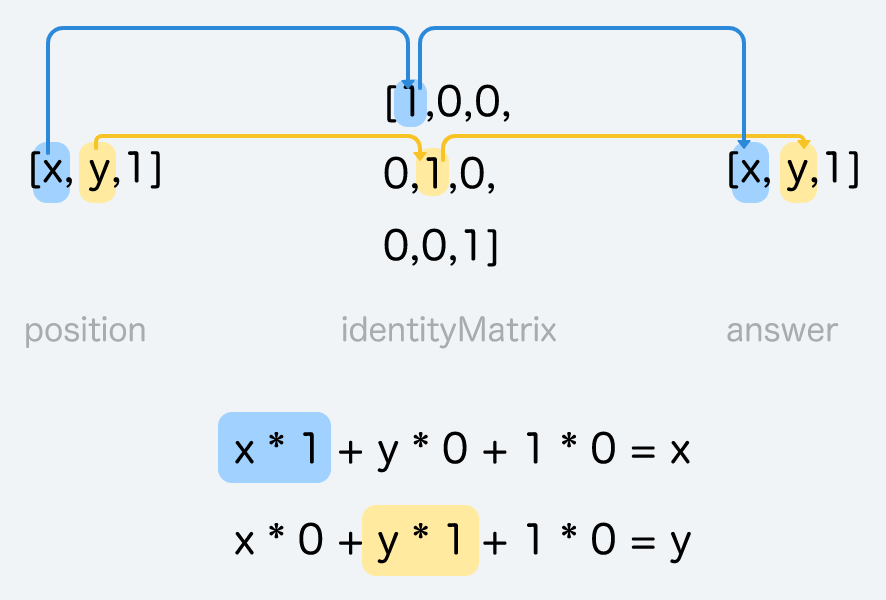
3. 天才準備了「單位矩陣」，用來乘以向量

   const identityMatrix = [1,0,0,
   						0,1,0,
   						0,0,1]
   

4. position與identityMatrix以相乘，結果會是自己！

   // 兩者計算：
   //           [x*1 + y*0 + 1*0,
   //			x*0 + y*1 + 1*0,
   //			x*0 + y*0 + 1*1]
   
   const answer = [x, y, 0]
   

   記得程式的欄列跟數學是相反的。數學用列乘以欄，程式用欄乘以列

   

5. 這個天才最大的發現是，若修改矩陣，就能位移！假設今天position 要位移 (tx,ty) 單位，至 (x+tx, y+ty)。

   const position = [x,y,1]
   
   // 假設今天要移動tx, ty
   const translation = [tx, ty]
   
   // 把tx跟ty放在特定的位置即可
   const translationMatrix = [1,0,tx,
   												0,1,ty,
   												0,0,1]
   
   // 兩者計算乘積：
   //           [x*1 + y*0 + 1*tx,
   //			  x*0 + y*1 + 1*ty,
   //			  x*0 + y*0 + 1*1
   //						]
   
   //最後位移了
   const answer = [x+tx, y+ty, 1]
   

   

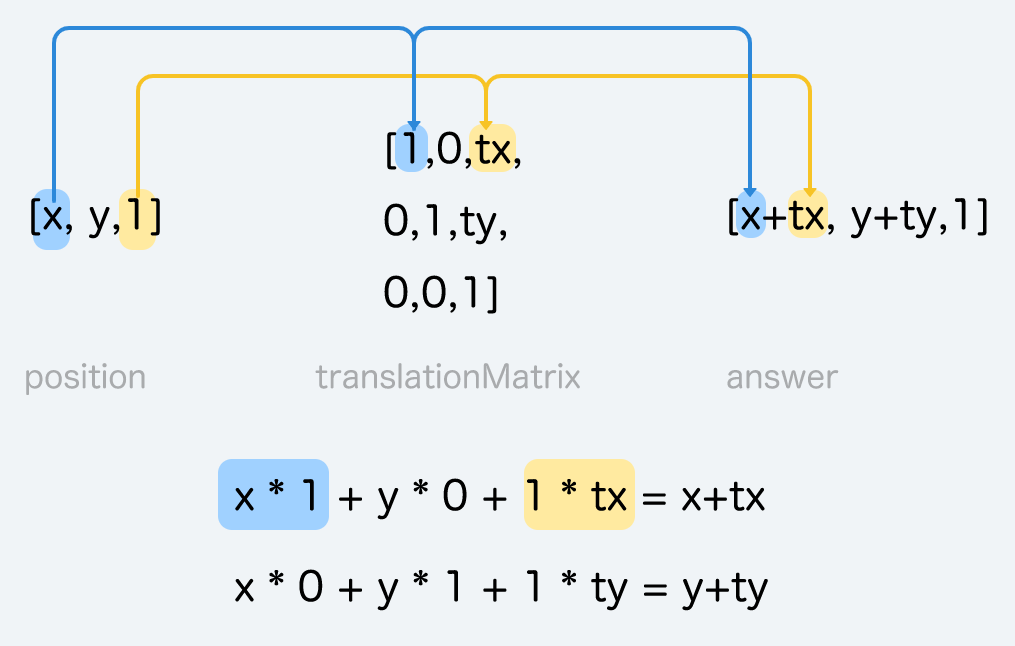
6. 這個天才利用矩陣位移了position。回顧他的作法：把tx放到陣列第七位，ty放到第八位。

矩陣：用來縮放

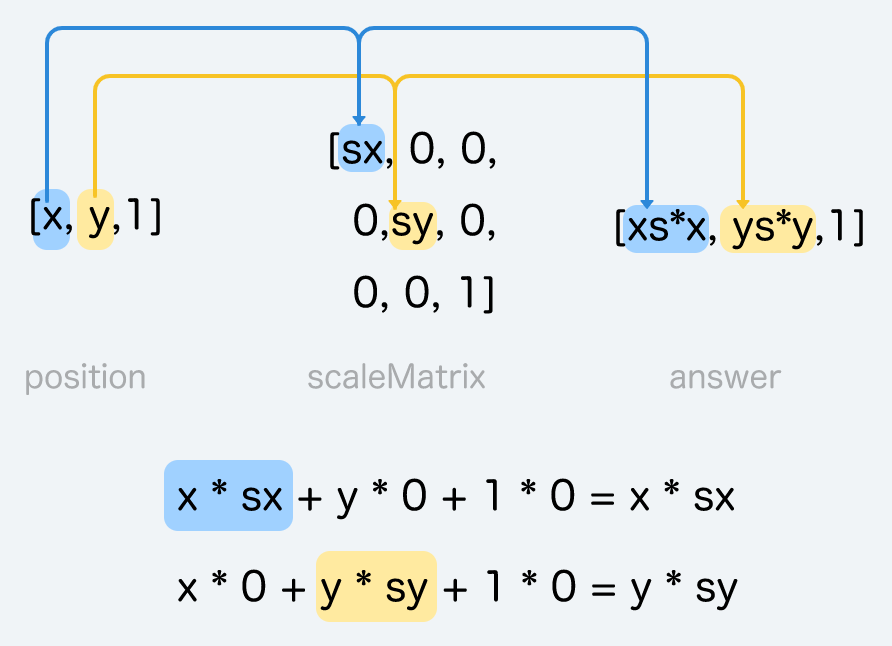
1. 接著，這個天才發現縮放的方法。假設今天position (x,y) 要縮放成 (xsx, ysy)：

   const position = [x,y,1]
   
   // 假設今天要縮放sx, sy
   const scale = [sx, sy]
   

2. 把sx, sy放到陣列第一位、第五位即可

   // 把sx, sy放在特定的位置即可
   const scaleMatrix = [sx,0,0,
   					0,sy,0,
   					0,0,1]
   

3. 接著計算

   // 兩者計算：
   //           [x*sx + y*0 + 1*0,
   //			  x*0 + y*sy + 1*0,
   //			  x*0 + y*0 + 1*1
   //						]
   
   //最後縮放了
   const answer = [xs*x, ys*y, 1]
   

   

矩陣：用來旋轉

1. 這個天才不善罷甘休，他找到了旋轉的方法。假設今天position (x,y) 要旋轉θ (假設移動90度，也就是1/4的PI)

   const position = [x,y,1]
   const θ = Math.PI / 4
   

2. 這個天才想到了旋轉的公式。

   const ax = x * cos(θ) + y * sin(θ)
   const ay = x * -sin(θ) + y * cos(θ)
   

3. 他端倪了一下，說了聲「那還不簡單」然後毅然決然的放在正確的位置

   const rotationMatrix = [cos(θ) ,sin(θ), 0,
   						-sin(θ),cos(θ), 0,
   					          0,     0, 1]
   

4. 經過計算，矩陣仍然完勝。

   // 兩者計算外積：
   //           [x*cos(θ) + y*sin(θ) + 1*0,
   //			 -x*sin(θ) + y*cos(θ) + 1*0,
   //			       x*0 +      y*0 + 1*1
   //						]
   
   const answer = [x*cos(θ)+y*sin(θ), x*-sin(θ)+y*cos(θ), 1]
   

   

• 因為篇幅關係沒有介紹旋轉的公式。我們先記住這個旋轉的公式就好了。之後再提到Shader時，旋轉的公式會再講解釋一遍。

在Three.js實作該方法

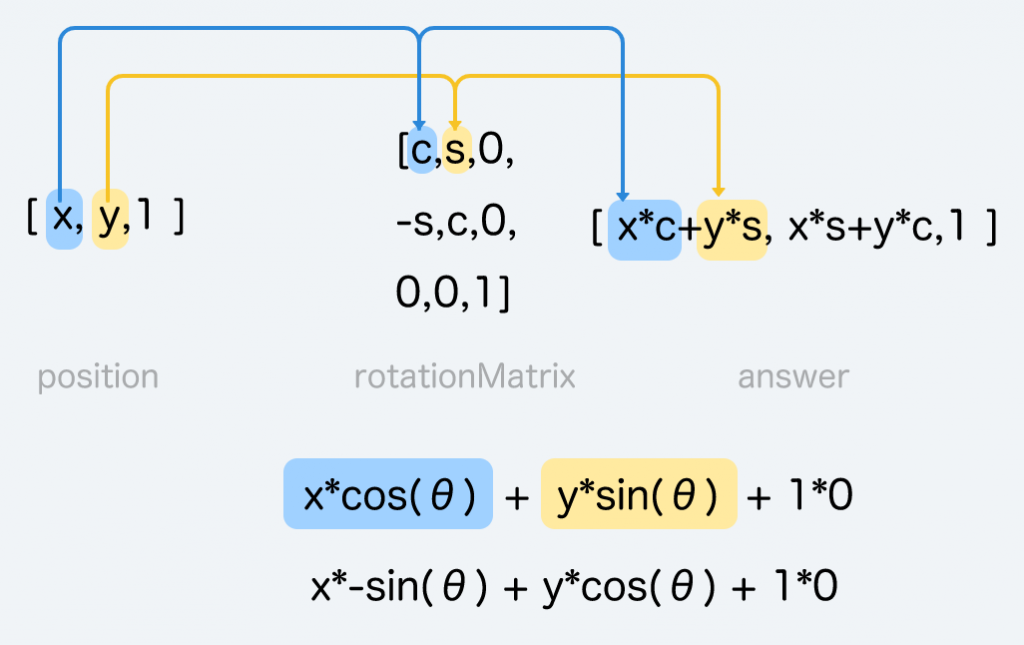
上面可以看出，位移、縮放、旋轉都可以用3x3的矩陣辦到。

這麼好用的東西，再也不用擔心形變的順序問題了。

我只要把參數放在矩陣的正確位置，無論多複雜，都可以用一個矩陣搞定！

Three.js身為強大的函式庫也不會放過這點，提供了一個物件，讓我們快速完成矩陣運算。

const matrix = new THREE.matrix4()

使用set()即可將我們的矩陣放上去，使用applyMatrix4() 能夠將此矩陣套用到cube上。

// 給定單位矩陣（不會有變化）
const matrixArray = [
	1, 0, 0, 0,
	0, 1, 0, 0,
	0, 0, 1, 0,
	0, 0, 0, 1
]
const matrix = new THREE.Matrix4().set(...matrixArray)
cube.applyMatrix4(matrix)

重新溫習一下位移：如果要將cube.position位移到(5,0,0)的話，要改成

const tx = 5
const ty = 0
const tz = 0

const matrixArray = [
	1, 0, 0, tx,
	0, 1, 0, ty,
	0, 0, 1, tz,
	0, 0, 0, 1
]
const matrix = new THREE.Matrix4().set(...matrixArray)
cube.applyMatrix4(matrix)

不僅可以放位移，還能再加上縮放

const sx = 2
const sy = 1
const sz = 1

const matrixArray = [
	sx, 0, 0, tx,
	0, sy, 0, ty,
	0, 0, sz, tz,
	0, 0, 0, 1
]
const matrix = new THREE.Matrix4().set(...matrixArray)
cube.applyMatrix4(matrix)

如此一來，無論是位移、縮放、旋轉，都可以在矩陣裡面完成。如果我們拿上一篇的程式碼來示範，那麼這是我們目前的成果。

CodePen

https://codepen.io/umas-sunavan/pen/JjvNYwY

＊請把31~46註解打開，把18、19行註解關掉

在Three.js實作：Matrix4的寫化寫法

每一次都要寫四排數字，也太麻煩了吧？

對，所以Matrix4提供幾個功能方便應用。

• makeRotationX, makeRotationY, makeRotationZ: 給定一個弧度，它將回傳全新的旋轉矩陣

  const rotateMatrix = new THREE.Matrix4().makeRotationY(Math.PI/4)
  cube.applyMatrix4(rotateMatrix)
  

• makeScale: 給定一個縮放倍率，它將回傳全新的縮放矩陣

  const scaleMatrix = new THREE.Matrix4().makeScale(2)
  cube.applyMatrix4(scaleMatrix)
  

• makeTranslation: 給定一個位移，它將回傳全新的位移矩陣

  const translationMatrix = new THREE.Matrix4().makeTranslation(5,0,0)
  cube.applyMatrix4(scaleMatrix)
  

注意，這些都是回傳全新的喔，所以新的會覆蓋舊的。

那要怎樣才能不互相覆蓋？再用乘的即可。

• multiply

  // 矩陣相乘
  const translationMatrix = new THREE.Matrix4().makeTranslation(5,0,0)
  const scaleMatrix = new THREE.Matrix4().makeScale(2,1,1)
  const combineMatrix = translationMatrix.multiply(scaleMatrix)
  cube.applyMatrix4(combineMatrix)
  

  

  即使我的旋轉跟位移調換，結果仍然一致：

  const translationMatrix = new THREE.Matrix4().makeTranslation(5,0,0)
  const rotateMatrix = new THREE.Matrix4().makeRotationZ(Math.PI/4)
  cube.applyMatrix4(translationMatrix.multiply(rotateMatrix))
  

  

在Three.js實作：錯誤情境

// 下面這樣順序仍然會有差異
const translationMatrix = new THREE.Matrix4().makeTranslation(5,0,0)
const rotateMatrix = new THREE.Matrix4().makeScale(2,1,1)
cube.applyMatrix4(translationMatrix)
cube.applyMatrix4(rotateMatrix)

// 這樣Translation就被Scale蓋掉了
const wrongMatrix2 = new THREE.Matrix4().makeTranslation(5,0,0).makeScale(2,1,1)
cube.applyMatrix4(wrongMatrix2)

在Three.js實作：附上CodePen

CodePen

可以註解掉我已經寫好的多種方法玩看看。

https://codepen.io/umas-sunavan/pen/JjvNYwY

當然，還有其他好用的函式：

Three.js矩陣的函式

進階旋轉函式

makeRotationAxis ：選定一個軸，以該軸旋轉（不限定純XYZ軸）

makeRotationFromEuler：以歐拉角旋轉（下篇介紹）

makeRotationFromQuaternion：以四元數旋轉

匯入匯出函式

extractRotation：給matrix4.extractRotation()一個Matrix參數，matrix4會把旋轉的部分解出來放到該參數裡面。

setFromMatrixPosition：給matrix4.setFromMatrixPosition()一個Matrix參數，matrix4會把位移的部分解出來放到該參數裡面。

setFromMatrixScale：給matrix4.setFromMatrixScale()一個Matrix參數，matrix4會把縮放的部分解出來放到該參數裡面。

compose 和 decompose：給它三個參數，它可以一口氣組成/解出位移、四元數與縮放

toArray：將matrix匯出成陣列

set：匯入陣列到matrix

進階操作函式

lookAt：給定eye跟target，會根據兩者的方向產生旋轉（up為上）

multiply：相乘matrix，可以用它將不同的matrix串在一起。

以上這些就是矩陣的介紹，希望能幫助大家問題。

想必你已經有疑問了，Quaternion 跟 Euler 到底是什麼？我不斷提及又不斷跳過。

明天我接下來將接著描述Quaternion 四元數跟 Euler 歐拉角，這將比矩陣更難理解，敬請期待。