圖片來源

艾斯卡諾在正中午最強，就如同three.js的光。你可能會覺得：

圖片來源

我可不是瞎掰喔，聽我解釋。

中午光線最強，就像艾斯卡諾中午最猛，而這是因為跟太陽的角度最小。一切都是角度！我們只要能夠釐清這一切，就能像艾斯卡諾一樣強！

黃猿那篇告訴我們，之所以能夠在3D創造光，是因為有內積。而內積之所以使我們的光線最強，正是因為面的法線角度，跟太陽光的角度最小。

而因為有了內積，我們才能在中午的時候最強大！一起來創造傲慢的太陽吧！

實作地球與太陽

有了上一篇的邏輯概念，我們得知：three.js封裝了幾個物件，使我們快速導入光。

我們以地球為例，示範該如何給地球照光。

實作地球與太陽：附上篇的codepen作開頭

我們一樣拿上一篇的程式碼。

https://codepen.io/umas-sunavan/pen/JjvJKJV

先把上次有關更新target的程式碼拿掉

 // 移除下面三行
- // 改用這個方法來控制鏡頭的方向
- control.target.set(10,0,0)
- control.update()

實作地球與太陽：新增太陽

作法跟地球一致，只是缺一張貼圖：

圖片來源

這裡有很不錯的星球材質可以使用，載入圖檔即可。

// 新增太陽
const sunGeometry = new THREE.SphereGeometry(5,50,50)
const sunTexture = new THREE.TextureLoader().load('2k_sun.jpeg')
const sunMaterial = new THREE.MeshBasicMaterial( { map: sunTexture, side: THREE.DoubleSide})
const sun = new THREE.Mesh(sunGeometry, sunMaterial);
scene.add(sun);

實作地球與太陽：把地球移到旁邊

移動position即可。

earth.position.set(20,0,0)

實作地球與太陽：新增DirectionalLight

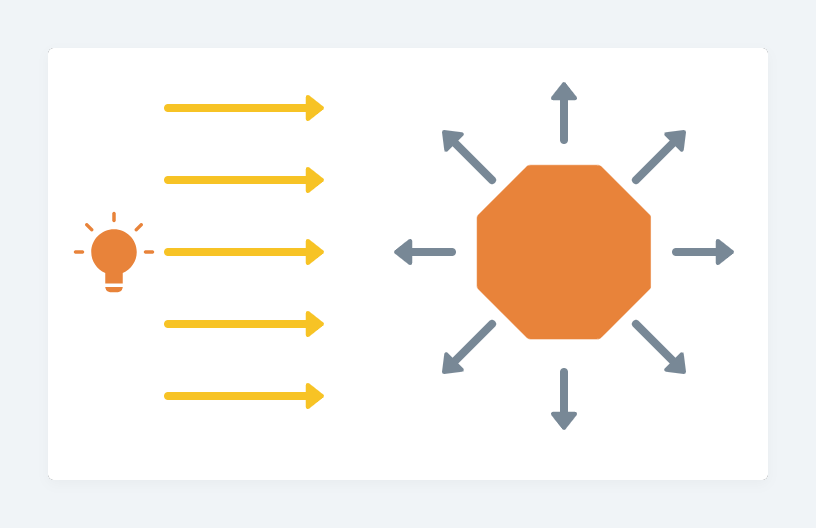
太陽系非常大，大到實際上照到地球的，就是平行光。我們先從平行光開始。

平行光就是DirectionalLight，先實例化它。

// 新增平行光
const directionalLight = new THREE.DirectionalLight(0xffffff, 1)
scene.add(directionalLight);
// 新增Helper
const lightHelper = new THREE.DirectionalLightHelper(directionalLight, 20, 0xffff00)
scene.add(lightHelper);
// 更新位置
directionalLight.target.position.set(20,0,0);
directionalLight.target.updateMatrixWorld();
// 更新Helper
lightHelper.update();

• Helper是什麼？
  • three.js 提供很多種Helper，顧名思義就是輔助你視覺化一些看不到的東西，例如鏡頭邊界、光的邊界。在這裡，DirectionalLightHelper幫我們視覺化平行光的方向跟位置
• 啊這裡怎麼也有target？
  • 這裡怎麼跟之前****Day6: three.js 圓弧的藝術家！弧線的教授！——軌道控制器****的OrbitControl一樣有target? 因為如同OrbitControl，DirectionalLight 也指向某一個目標，我們必須設定。
• updateMatrixWorld()是什麼？
  • target設定之後，它預設不會更新。我們必須手動更新，所以執行updateMatrixWorld()。

這樣就完成了，非常簡單。

CodePen

https://codepen.io/umas-sunavan/pen/yLjoqNg?editors=1010

實作地球與太陽：點光的太陽

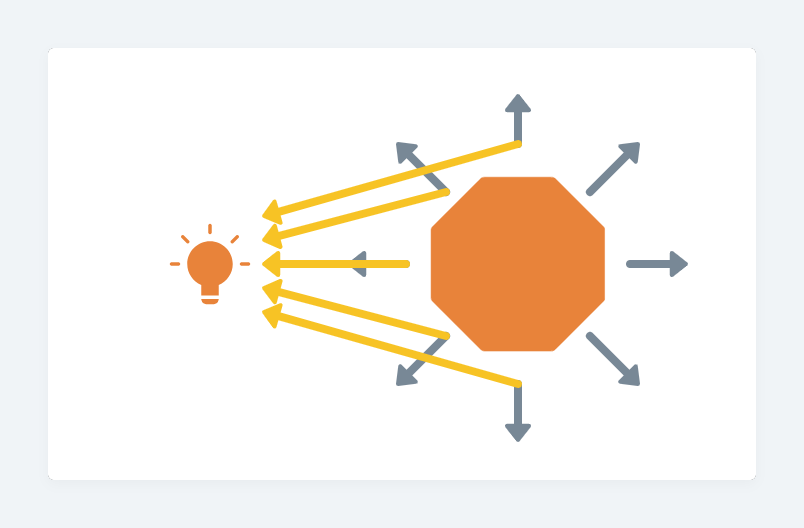
雖然說太陽照到地球時幾乎是平行光，但實際上，太陽是一個點光。我們來實作看看點光的太陽。

- 新增平行光
- const directionalLight = new THREE.DirectionalLight(0xffffff, 4)
- scene.add(directionalLight);
- // 新增Helper
- const lightHelper = new THREE.DirectionalLightHelper(directionalLight, 20, 0xffff00)
- scene.add(lightHelper);
- // 更新位置
- directionalLight.target.position.set(20,0,0);
- // 更新Helper
- lightHelper.update();
+ // 新增點光
+ const pointLight = new THREE.PointLight(0xffffff, 1)
+ scene.add(pointLight);
+ // 新增Helper
+ const lightHelper = new THREE.PointLightHelper(pointLight, 20, 0xffff00)
+ scene.add(lightHelper);
+ // 更新Helper
+ lightHelper.update();

比較不同的是，點光沒有方向，是四射的，所以沒有target。

可以看到，光在地球的上方跟下方變得比較暗，因為這兩端的面其法線與向光的線夾角過大，導致在內積的計算結果很小。

我已經把地球拉到太陽旁，幾乎世界末日的距離了，相信大家可以看出差別。

CodePen

https://codepen.io/umas-sunavan/pen/WNJEKZo

以上就是太陽光源的實作。

等一下，你都沒介紹RectAreaLight呢！

我介紹平行光、點光、聚光燈（本質是點光）、環境光、半球光，但就是沒有介紹矩形區域光。

矩形區域光很有趣，它可以模擬窗戶進入室內的光。

我沒有找到實際上的程式碼，但有找到有神人實作區域光的過程。

兩種光的合體

根據它的過程，區域光同時有點光，也有平行光的特性。

意思是，一個物體如果都在矩形區域光的投影範圍內，它是平行光。但如果它為位在區域範圍外，它就是點光。而這個邏輯又該怎麼實作呢？也同樣的是內積嗎？

先看看原文：

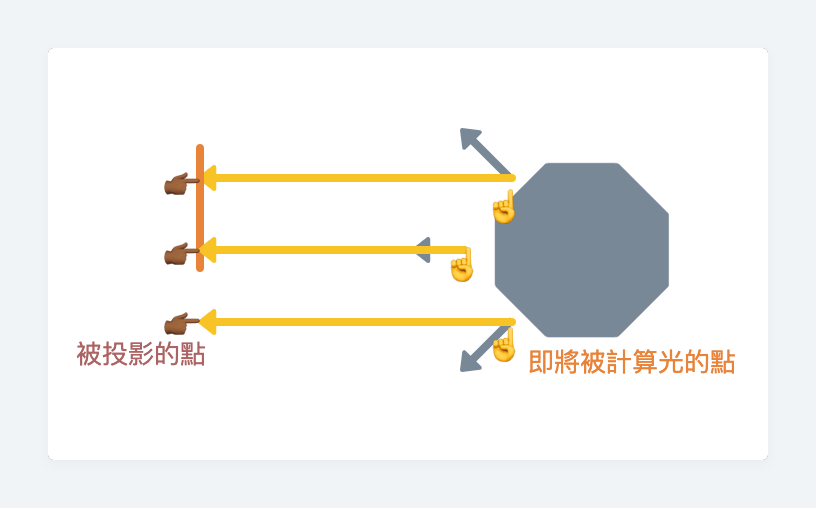
Step 1.- Project the soon-to-be-shaded point on the plane that contains the area light.
// 將「即將被計算光的點」投影到發光的平面上，以找到面上「被投影的點」

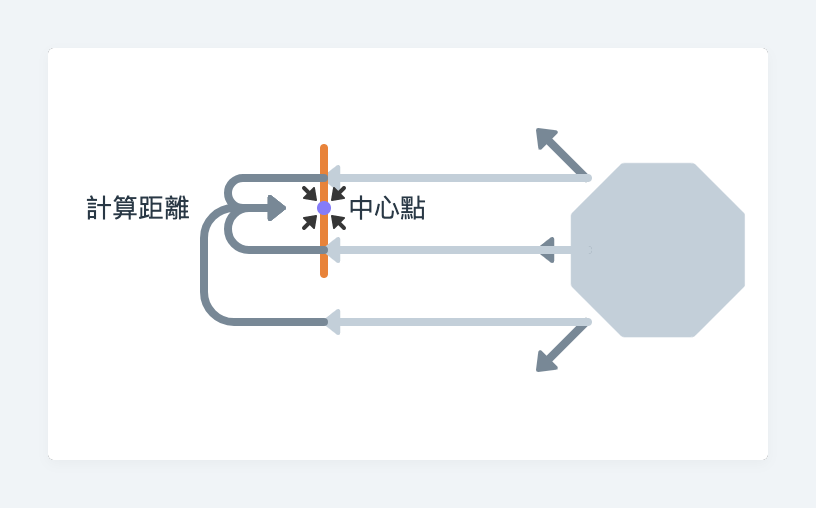
Step 2.- Calculate distance from the center of the rectangle to the projected point.
// 計算發光面的中心到面上被投影的點的距離

Step 3.- Obtain 2D coordinates of the projected point on the plane (how do you call this? the area´s object space?) using the distance calculated in (2) along with area height and width.
// 取得「被投影的點」位在發光面的平面座標

Step 4.- Clamp the projected point in 2D so that it lies inside the area.
// 如果投影過去不在面上，那就取到面上。

Step 5.- This is the area point that lies nearest to our point. Retrieve distance between both points, using the width and height of the area to take back the nearest point to eye-space. This is used to calculate attenuation as usual.
// 接著就可以找到「被投影（且取到面上）的點」，也可因此計算「即將被計算光的點」對它的距離。
// 用發光的面其寬高來把最近的點帶回鏡頭視線（這句我其實也看不太懂），而這也用來計算光的衰減。

Step 6.- In an area light each point is shaded from several directions at once, to simulate this multiply the usual dot product between normal and light direction by a factor and clamp it, so that you get a range of normals that get maximum illumination, then a smooth decay as they turn away from the light.
// 計算「被投影（且取到面上）的點」與面的normal（可理解為法線）的內積。剩下的句子我也不太能理解，但至少我們理解其光的計算方式。

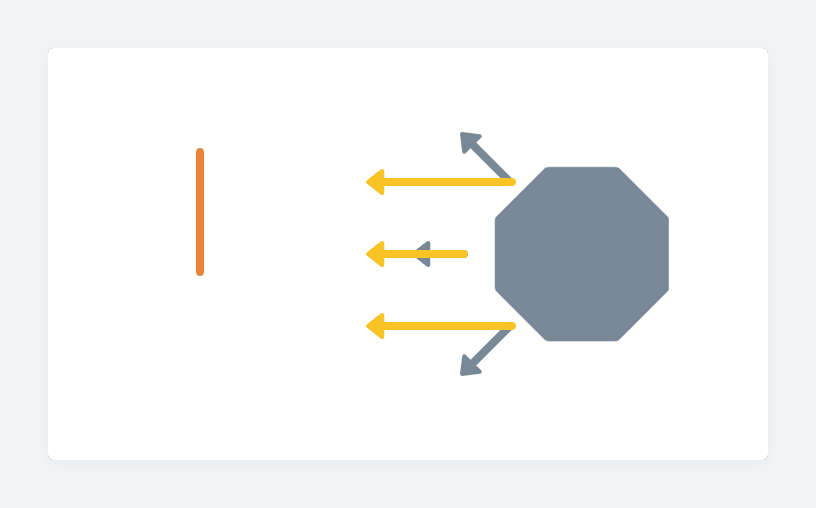
首先，有一個區域光投影在物體上

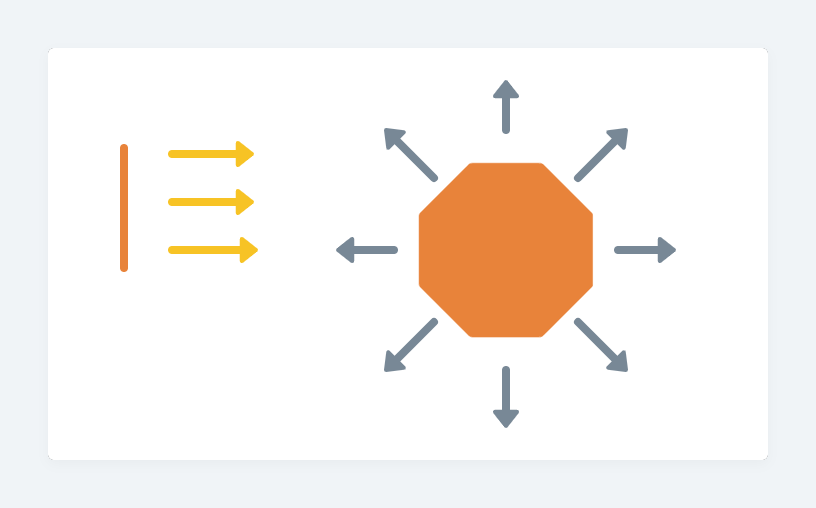
光投向面，就如同面投向光。我們以這三點為例好了

第一步：將「即將被計算光的點」投影到發光的平面上，以找到面上「被投影的點」

第二步：發光面的中心到被投影的點的距離

第三步：取得「被投影的點」位在發光面的平面座標

第四步：如果投影過去不在面上，那就取到面上。

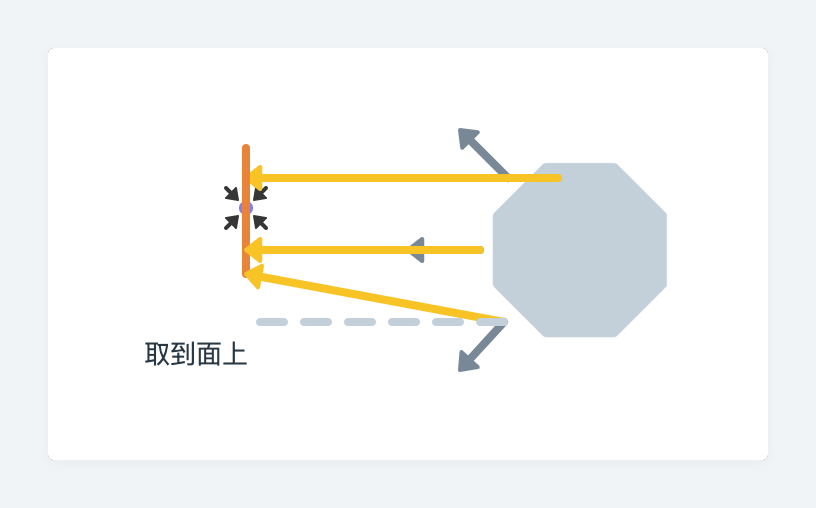
第五步：找到「被投影（且取到面上）的點」，也可因此計算「即將被計算光的點」對它的距離。

第六步：計算「被投影（且取到面上）的點」與面的normal（可理解為法線）的內積

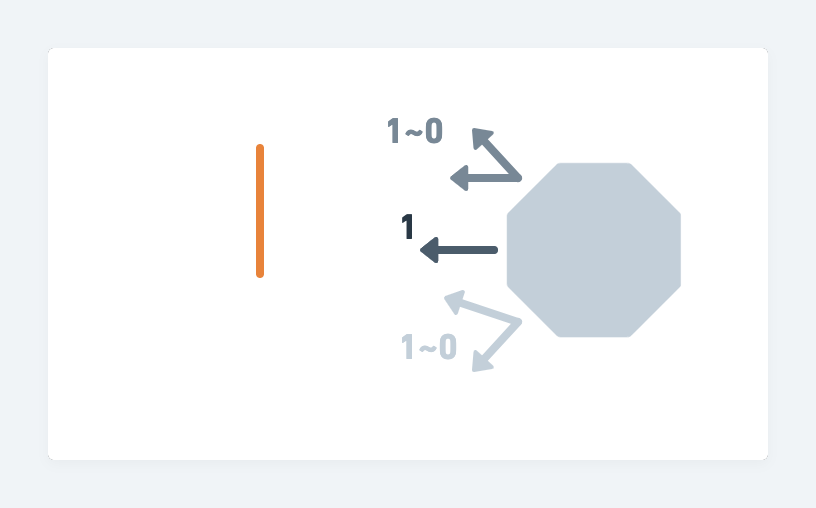
如此一來，光就完成了。

從此圖我們可以觀察到，在投影範圍內的物件，向光的單位向量是同方向的，等同於平行光。而不在投影範圍內的物件，其向光的單位向量是不一致的，等同於點光。

不在投影範圍內的面，它在三個點的亮度排名中第三名。這是因為它投影到面上面的點，被移動了，而這樣的移動導致它向光的角度有所改變，角度較大，也導致後續在向量的計算中，內積數值最小。

釐清光的原理對於視覺特效有什麼用？

1. 光是向量計算非常實用的運算過程，我們在後續WebGL Shader的製作當中，如果有這樣的概念，要製作自製的特效有非常大的幫助。這道理就如同：一個設計師若理解了圖層、錨點工具或是混合模式之後，不管是Photoshop、illustrator、figma都可以得心應手。
2. 即使我們脫離了three.js的知識領域，到了babylon、webGL或是其他領域時，也可以知道它底層的概念，並且快速上手。

附上所有常用光源的程式碼

程式碼裡面的物件是我自己建模的，可以自行取用。

CodePen

https://codepen.io/umas-sunavan/pen/xxjXggj?editors=1010

下一步

接下來，我將介紹貼圖，進入貼圖的領域。

參考資料：

頂點法向量

矩形區域光的解釋

WebGL 3D - Directional Lighting