R squared (R平方)

R平方(R squared)又稱為判定係數(coefficient of determination)
是一種衡量回歸模型表現的指標
R平方公式：
R^2 = 1 - SSres/SStot

這邊借用一下上課教材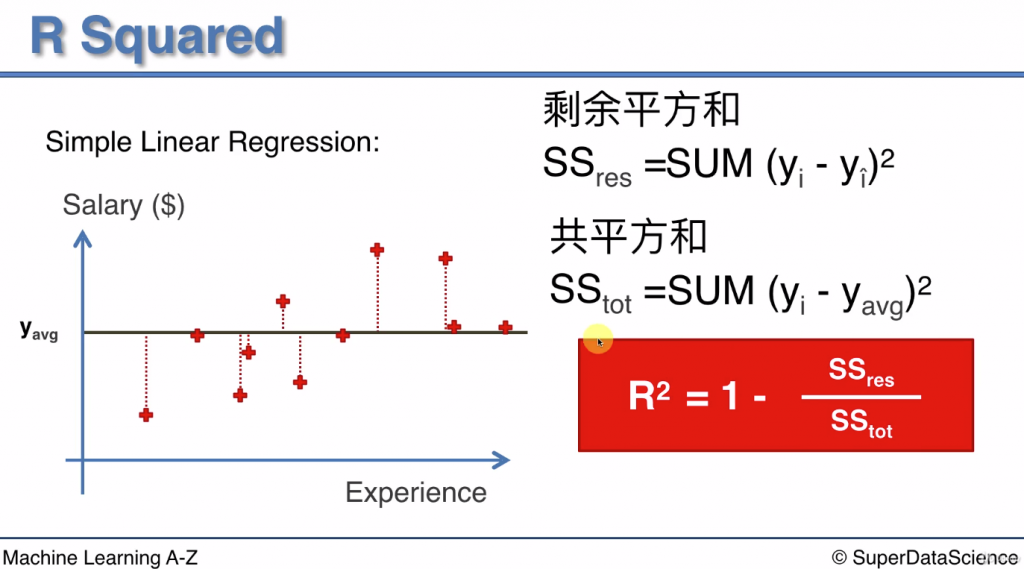

SSres

SSres = residual sum of squares 殘差平方和 or 剩餘平方和
之前就有提過剩餘平方和的概念
將所有預測值與實際值的差平方後相加即為剩餘平方和
當剩餘平方和越小, 代表預測值越接近實測值
因此當得到一個最小的剩餘平方和, 代表擬合出一條最佳模型了(對模型解釋度高)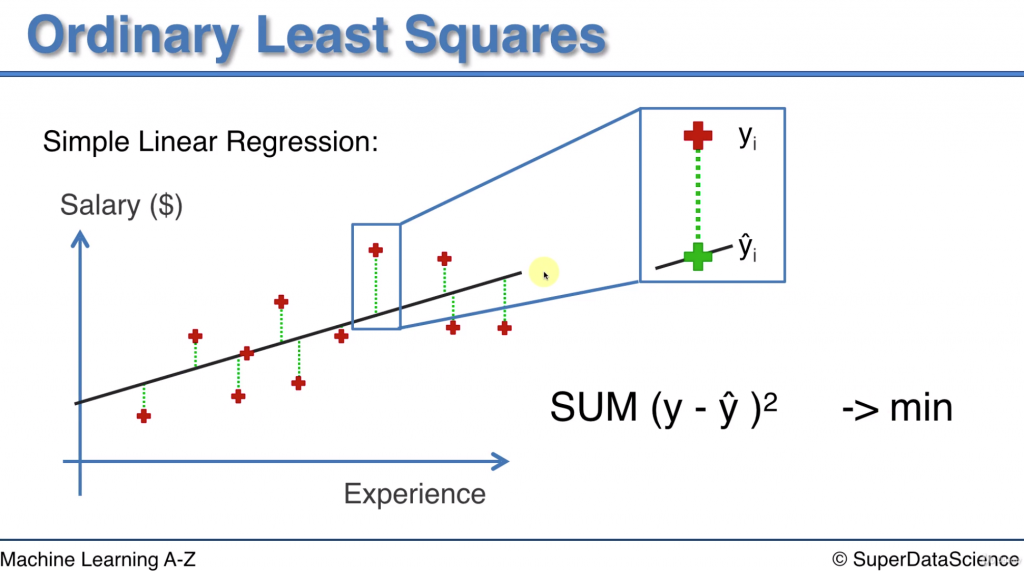

SSres 會大於SStot嗎？
有可能, 當SSres 算出來的模型很糟, 完全無法代表這些點的時候
就會比用平均值還要糟糕, 此時SSres/SStot > 1, ㄏ就會是負的
不過我們目前使用的線性回歸模型不會有這種問題
所以 SSres < SStot --> R平方介於[0,1]之間

SStot

SStot = total sum of squares 總平方和
我們將所有點的y值取平均, 畫出一條水平線當作模型
則所有實際值與平均值的差平方後相加即為總平方和

SStot 有機會為0嗎？
答案是不會, 因為不會有資料y全都一樣的情況出現(若資料y全都一樣, y(avg)也會等於y)
所以R平方不會有分母SStot為０的除法問題

R平方可能為1嗎？

有, 當SSres = 0 的時候 R平方會等於1
而SSres什麼時候會等於0?
代表預測值跟實際值完全一模一樣的時候, 使得差值為0

Reference

回歸分析(Regression analysis)的R平方(R squared)與調整後R平方(Adjusted R squared)
https://medium.com/qiubingcheng/%E5%9B%9E%E6%AD%B8%E5%88%86%E6%9E%90-regression-analysis-%E7%9A%84r%E5%B9%B3%E6%96%B9-r-squared-%E8%88%87%E8%AA%BF%E6%95%B4%E5%BE%8Cr%E5%B9%B3%E6%96%B9-adjusted-r-squared-f38ad733bc4e