The Gaussian RBF Kernel

今天要學習 高斯RBF kernel function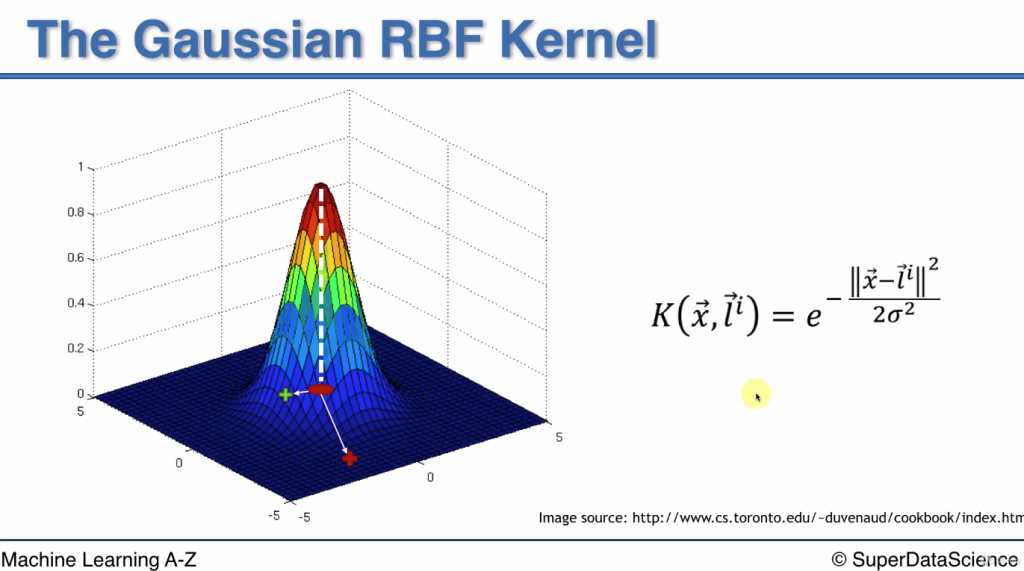

此函數在二維空間中的圖像就像一座山
(0,0) 在圖中是最高點1
離(0,0)越遠高度越小, 例如到(-5,-5), 高度變成0

假設l是中心點, x 是周圍取的一個點(圖中的紅色or綠色叉叉)
公式就相當於是e的負數(負數的分子是x與l的距離平方, 分母是常數zigma平方)
因此x距離越遠, 此負數越小, e的負數越趨近0
當x 等於l, 此負數=0, e的0次方就等於1
所以會看到圖型是一個山狀

因此我們可以利用這個公式的特性來解決左邊的問題：
L(landmark) 可以想像成中心的紅點
所有的綠點離中心點都小於一個常數
所有的紅點離中心點都大於一個常數
我們可以用一個圈圈把綠點跟紅點切開

圈圈內的點就相當於右邊山腳下的白色圈圈-> 也就是”分類邊界“

Zigma 的用處？

Zigma 可用來控制圈圈的半徑
當zigma 越大, x與l的距離也就越大
當zigma 越小, x與l的距離也就越小

zigma是由數據本身決定的
也就是綠色的點分布的離中心點多遠, zigma就多大

another problem

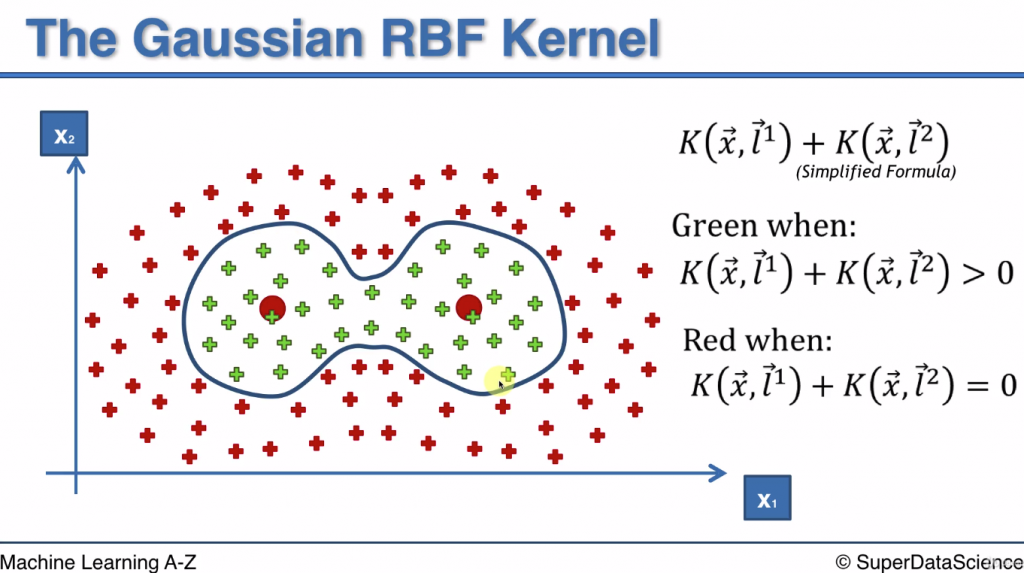
再看一個二維平面的問題, 一樣有兩種顏色的點
這組資料會有兩個中心點, 分別是l1, l2
而我們就繞著這兩中心點畫出分類邊界(8字型的線)
如圖右邊表示的, 這樣的邊界可以用兩個RBF 相加的函式來達成

明天會繼續看除了高斯RBF還有哪些kernel function 可以用