SVM(Support Vector Machine)

SVM又叫：支援向量機

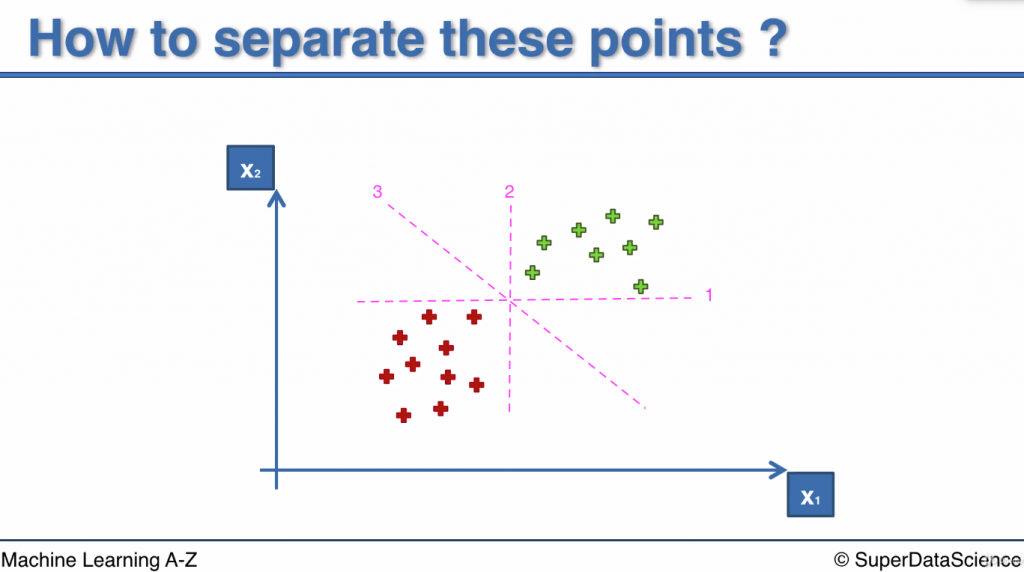
有一個二維平面(如上圖), 上面的點是訓練集裡的所有資料
紅色代表結果為0, 綠色代表結果為1
現在我們想找到一條分割線把紅色和綠色點分開
這樣的分割線可以是水平的, 垂直的, 或是對角的(如圖裡的線1,2,3)

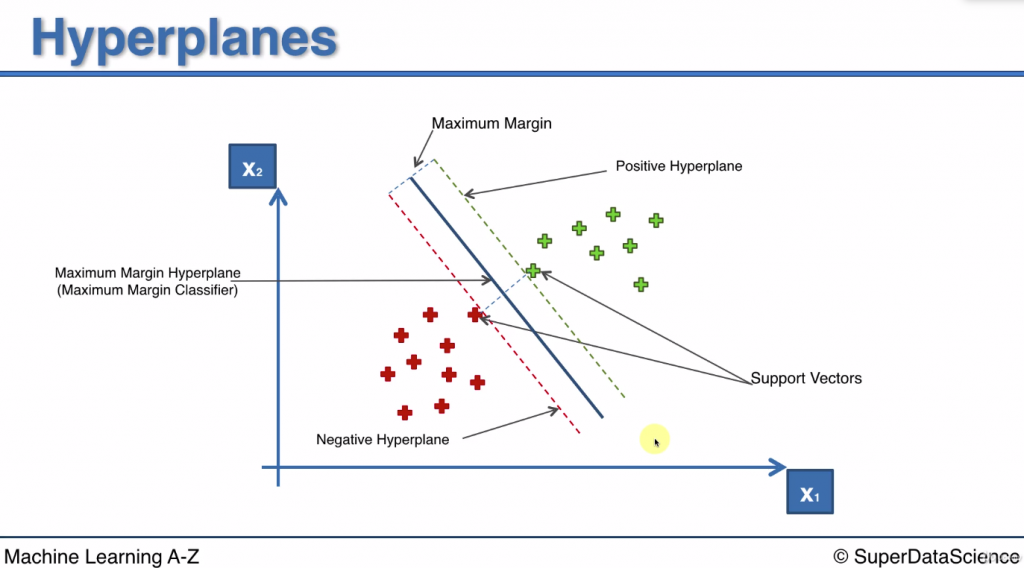
而使用 SVM 演算法會得到一條分割線
這條線和紅組/綠組中最近的點有最大間隔(Max Margin)

數學上來說
紅點距離直線=d(red)
藍點距離直線=d(green)
當畫出一條候選線, 可以得到 margin = min(d(red),d(green))
然而我們有很多候選線可以切開紅藍數據, 會得到很多個margin
其中有最大margin的那條線就是最佳分割線

關於距離最佳分割線最近的兩個點, 又稱為support vectors
因為：

1. 這兩個點支持這條分割線(其他的點就算移動位置, 這條分割線也不會改變, 只有這兩個點移動才會影響這條分割線)
2. 這兩個點本質上都是向量, 尤其在高維度的空間上, 更可以用向量來代表一個點

這條分割線又叫 Maximum Margin Hyperplane: 最大間隔超平面
(比數據空間小一維, ex: 二維空間下他就是一條直線, 三維空間下他就是一個平面)

和超平面平行的兩條線稱為Positive Hyperplane & Negative Hyperplane

What's so special about SVMs

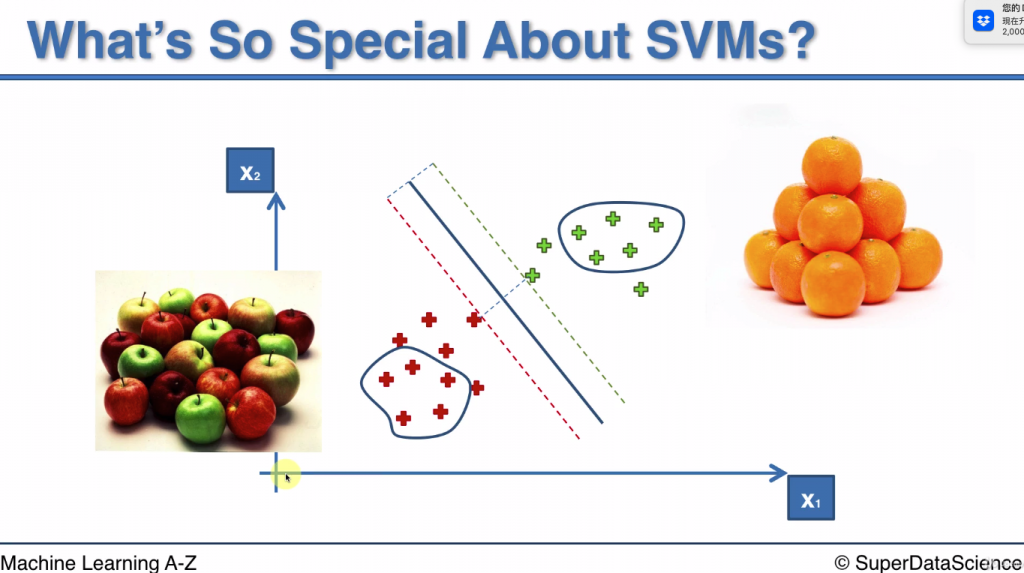
假設我們需要模型幫忙區別出蘋果和橘子, 且模型裡的x1 跟顏色特徵有關
當x1 越高, 代表顏色越接近橘色, 越容易被判定成橘子
當x1 越低, 代表顏色越接近紅色, 越容易被判定成蘋果

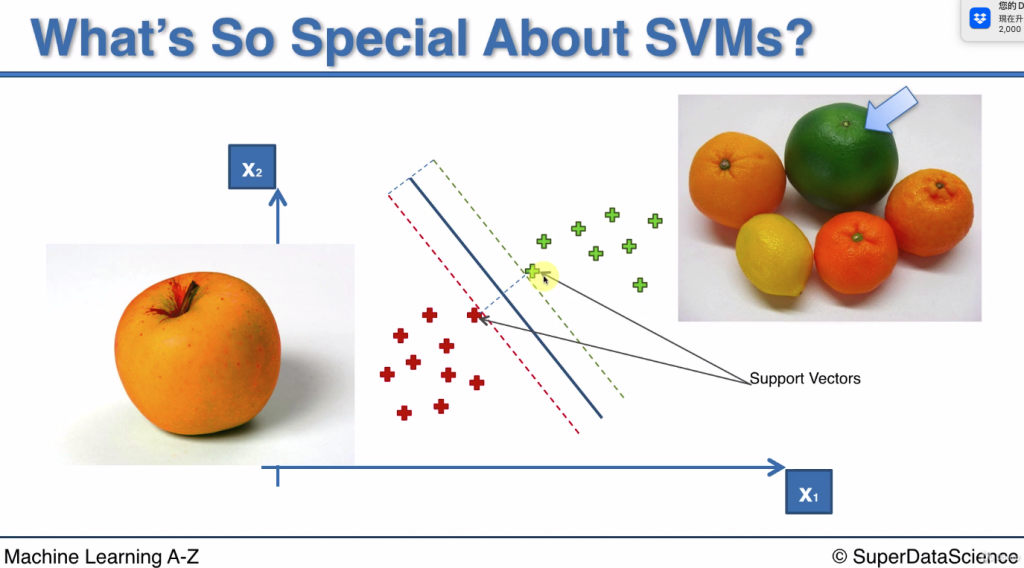
當今天出現一顆綠色的橘子, 那這顆橘子代表的就是綠色Ａ點, 因為特徵接近紅色點
當今天出現一顆帶有橘點的蘋果, 那這顆蘋果代表的就是紅色Ｂ點, 因為特徵接近綠色點
而這兩個點正是用來計算計算max margin的點
因此ＳＶＭ最特別的地方就是他是用極端的個體來計算的

Reference
本頁的圖片一樣擷取自Machine Learning A-Z 上課的教材