由於類神經網路在訓練時，會以線性的模式進行求解，但實際的問題經常為非線性的，為了減少線性程度，使得類神經網路的分析結果可更準確，激勵函數(Activation Function)便可於此使用，以增加類神經網路訓練時的非線性程度。常被使用的激勵函數包含了ReLU, SeLU, Softmax和Sigmoid函數，下面將逐一介紹。

(1) ReLU (Rectified Linear Unit)
ReLU為目前最常被使用的激勵函數，數學式型態可表示為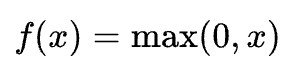

ReLU圖形如下圖所示：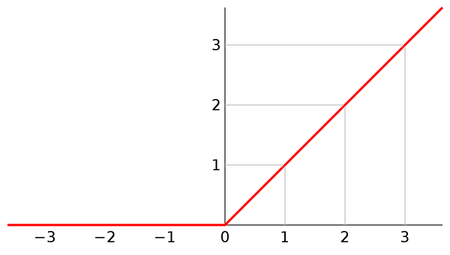

圖片來源：連結
由圖中可得知，若輸出值為正值，該輸出值經過ReLU函數轉換仍可正常輸出，若輸出值為負值，則經過ReLU函數轉換後，輸出值為0。
ReLU可增加類神經網路的稀疏性，可有效減緩過擬合(Overfitting)的狀況發生，也可解決梯度爆炸或梯度消失等問題。

(2) Sigmoid
Sigmoid數學式型態可表示為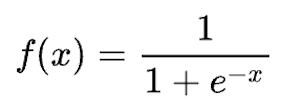

Sigmoid圖形如下圖所示：

圖片來源：連結
Sigmoid函數適用於二元分類(Binary Classification)，其非線性且梯度平穩的特性，使得其可做為良好的激勵函數，但當輸入值有離群值時，經過Sigmoid函數輸出並不能反映出該值是否為離群值，也具有梯度消失的潛在問題。

(3) tanh
tanh數學式型態可表示為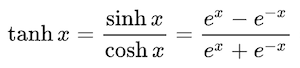

此函數圖形與Sigmoid函數某種程度上相似，但由於其範圍為[-1,1]，因此輸出的理論平均為0，收斂速度較Sigmoid快。與Sigmoid相同，tanh一樣有著梯度消失的潛在問題。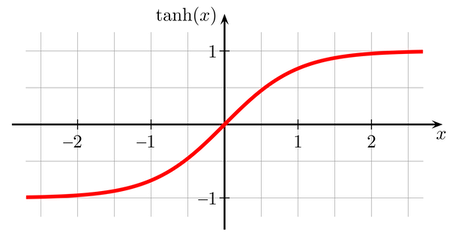

圖片來源：連結

(4) Softmax
Softmax數學式型態可表示為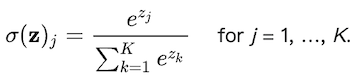

Softmax圖形如下圖所示：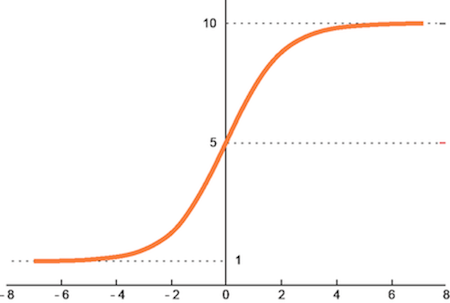

圖片來源：連結
Softmax函數可用於解決多元分類的問題，在計算各種類別發生的機率分布時，所有機率的總和會等於1。但若是有離群值時，經過Softmax轉換後數值會有更偏離的現象，因此在進行複雜影像辨識時，並不是一個好用的激勵函數。