在介紹完Backtracking後，我們接下來要介紹動態規劃的攻略。
在解動態規劃或是Backtracking的題目時，我們都會用到決策樹(decision tree)，因為它可以很清楚的呈現遞迴（選擇）的過程。

為什麼動態規劃

當一個問題可以被拆分成更小的子問題時，並且這些子問題的答案如果能幫忙解決問題的話，最直觀的解法是利用遞迴來解題。但是為了得到更好的時間複雜度這時候就可以嘗試使用動態規劃。動態規劃就是用來提升遞迴演算法的效能的。而這類型的動態規劃也被稱為Memoization。

來看一題吧

Leetcode 509. Fibonacci Number
很有名的遞迴問題，他的base case和遞迴關係如下：

F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.

我們將他的遞迴關係視覺化：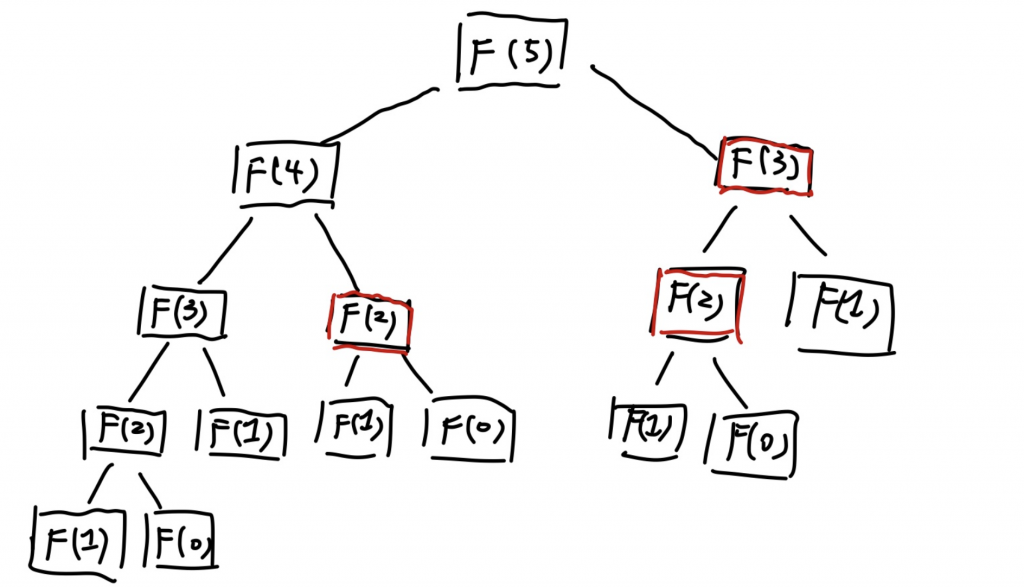

我們會發現有許多地方在遞迴時會重複計算（紅色框框），若是能將已經計算好的子問題「存起來」，當再次遇到相同的子問題時，我們即可以直接去access到這些答案，這就是memoization。

class Solution:
    def fib(self, n: int) -> int:
        cache = {}

        def dfs(i):
            if i <= 1:
                return i
            if i in cache:
                return cache[i]
            
            cache[i] = dfs(i - 1) + dfs(i - 2)
            return cache[i]
        
        return dfs(n)

上述的程式碼利用dictionary去儲存已經被計算的子問題，當遇到相同的子問題時直接將value return回去。

如果利用遞迴搭配hash table的叫做memoization，那麼不使用遞迴而是直接使用回圈來解題的就是True Dynamic Programming。
我們已經知道F(n)是由F(n - 1) 和F(n - 2) 得來的，那麼我們只要不停的去紀錄目前的子問題的前兩個子問題就能解決問題。

class Solution:
    def fib(self, n: int) -> int:
        dp = [0, 1]
        if n <= 1:
            return dp[n]
        
        for _ in range(2, n + 1):
            tmp = dp[1]
            dp[1] = dp[1] + dp[0]
            dp[0] = tmp
        
        return dp[1]

不同類型的決策樹

剛才我們所看到的範例，每一個節點都依賴他的左子樹和右子樹，但是並不是所有的問題都是這樣的。有時候我們需要比較左右子樹，根據題意決定使用哪邊的值來得到目前這個node的最佳解。

Example

Leetcode 322. Coin Change
給予一些不同幣值的硬幣，和一個目標的金額。要如何找出用「最少數量」的硬幣就能符合此金額？如果湊不出來就return -1。

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

分析：

1. 我們假設左子樹是選擇使用當前硬幣1次，並且讓目標金額扣除此幣值；右子樹代表不再使用這個幣值的硬幣了
2. 要使用當前幣值的硬幣，首先amount要大於等於這個幣值
3. 比較左子樹回傳回來的次數和右子樹回傳回來的次數誰比較少，比較少的次數會被繼續回傳回去。
4. Base case為目標金額降為零，代表我們確實找到一種方法可以湊成目標金額；以及當我們已經使用過所有可選擇的硬幣了，但是仍湊不出目標金額，這時候代表本題無解，我們回傳無限大來表示這條path無解。

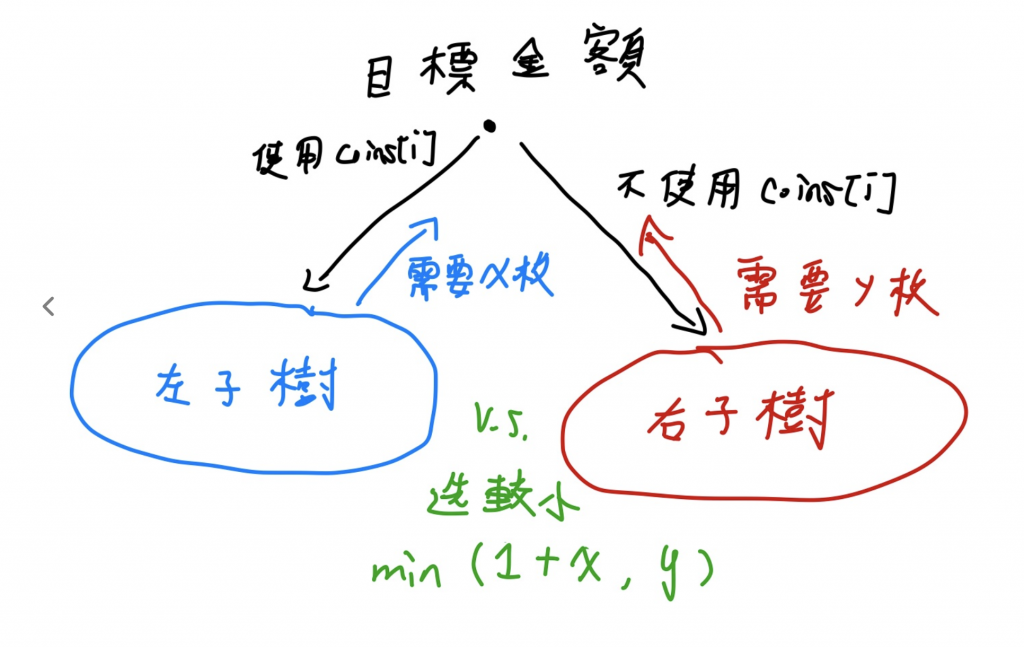
以下為Python程式碼實作

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        cache = {}

        def dfs(i, amount):
            if amount == 0:
                return 0
            if i == len(coins):
                return float('inf')
            if (i, amount) in cache:
                return cache[(i, amount)]

            # choose to use i-th coin
            choose = float('inf')
            if amount - coins[i] >= 0:
                choose = dfs(i, amount - coins[i]) + 1
            
            cache[(i, amount)] = dfs(i + 1, amount)
            cache[(i, amount)] = min(cache[(i, amount)], choose)
            return cache[(i, amount)]
        
        count = dfs(0, amount)
        return count if count != float('inf') else -1

後記：如果看到一個陌生的女生想要認識她，你需要在幾秒內去和她搭話，否則你會想太多錯失機會。如果你刷leetcode花了十分鐘卻不知如何下手，就應該直接去找答案來學習。By 我的強者朋友Jackson