今天要繼續攻略1D動態規劃，所謂的1D指的是我們可以用一維的陣列儲存子問題的解或表達子問題。
並且今天會著重使用True Dynamic Programming(Bottom up)的方式解題。
另外，關於何時使用動態規劃解題：當看到{subarray, substring}搭配{longest, shortest, maximum, minimum}時，可以優先考慮使用動態規劃。這部分我們在解題時會再提到。

好了，那我們就繼續解題吧：）

Leetcode 322. Coin Change

這題我們昨天用Memoization解過，今天要用Bottom up的方式來解。
題目敘述：給予一些不同幣值的硬幣，和一個目標的金額。要如何找出用「最少數量」的硬幣就能符合此金額？如果湊不出來就return -1。
Example:

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

以上述的範例，我們知道11可以由5, 5, 1湊出，我們假設dp[n]代表額度為n需要花費最少的數量的硬幣來湊出n。那麼dp[11]就是我們要求的解。那麼dp[11]可能是：

• dp[10], 搭配1元硬幣
• dp[6], 搭配5元硬幣
  比較出較少的方法數，極為答案。
  而dp[10]和dp[6]又可以由較小dp[n]得出，所以我們會從n = 1到n = 11，計算不同的dp[n]並且保存他們。

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf') for _ in range(amount + 1)]
        dp[0] = 0
        coins.sort()
        
        for a in range(1, amount + 1):
            for c in coins:
                if a - c >= 0:
                    dp[a] = min(dp[a - c] + 1, dp[a])
                else:
                    break
        
        return dp[-1] if dp[-1] != float('inf') else -1

注意：我們需要先把coins這個array以遞增的方式排序，因為當硬幣的幣值比當前的額度大時，就不用再繼續下去了。

Leetcode 213. House Robber II

題目敘述：有個小偷要去一個排列成環狀的房子裡偷錢，每棟房值裡面都有一些現金。但是小偷不能如果偷了某間房子裡的錢就不能偷與這間房子相鄰的房子裡的錢。請問小偷最多能偷到多少錢。
示意圖：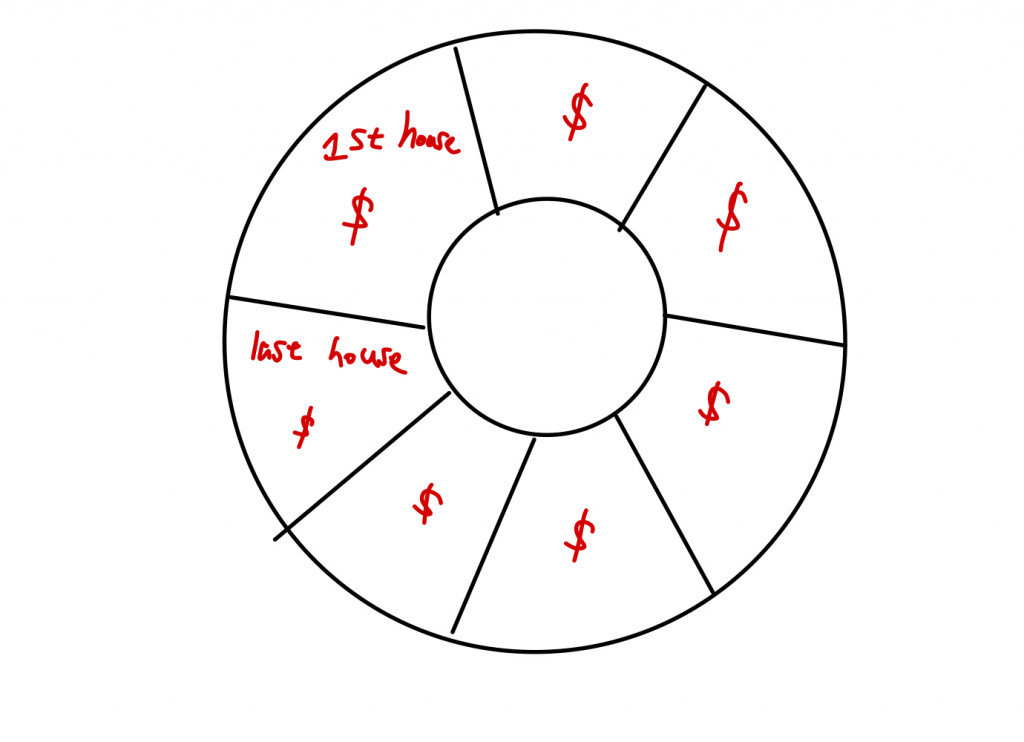

分析：如果我們可以把環狀變成一列那麼我們就有一個明確的頭和尾接下來只需要考慮子問題之間的關係，所以我們把圓環拆成兩種列，一條是包含了第一間房子的，另一條是包含了最後一間房子的。因為這兩間房子的選擇是互斥的（選了其中一間就不能選另一間）。這兩列就包含了所有的選擇方式。下圖是包含了第一間房子的列。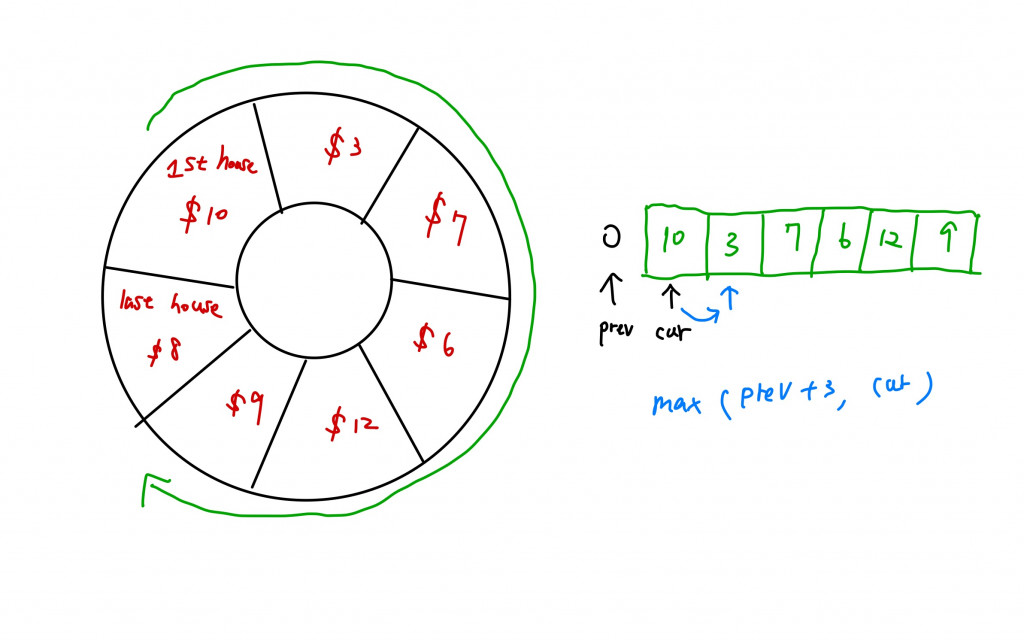

現在我們只需要解決子問題間的關係，在選擇是否要偷第i間房子時，我們要考慮的是不偷這間，那小偷目前偷到的總額就和偷到i - 1間房子的總額一樣；如果偷了這間房子裡的錢那小偷所偷到的總額就是這間房子裡的錢加上偷到第i - 2間房子所累積的錢。

以Python程式碼實作：

class Solution:
    def rob(self, nums: List[int]) -> int:
        if len(nums) == 1:
            return nums[0]
        forward = nums[:-1]
        backward = nums[1:]

        prev, cur = 0, forward[0]
        res = 0
        for i in range(1, len(forward)):
            tmp = cur
            cur = max(cur, prev + forward[i])
            prev = tmp
        
        res = cur
        prev, cur = 0, backward[0]
        for i in range(1, len(backward)):
            tmp = cur
            cur = max(cur, prev + backward[i])
            prev = tmp

        return max(res, cur)

注意：當房子只有一間時，我們不需要再分割第一間和最後一間房子，因為第一間就是最後一間，我們一定會選他。

Leetcode 53. Maximum Subarray

你看到題目的名字了嗎，有Maximum又有subarray，就可以把動態規劃當作預選的解題的手段。

題目敘述：有一整數input array，找出這個array中總和最大的subarray。subarray就是array某段連續的序列。
Example:

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: The subarray [4,-1,2,1] has the largest sum 6.

分析：如果前面累加的值和你現在正在拜訪的數值相加後比目前正在拜訪的數值還大那就應該繼續累加；相反的若是前面累加的數值和正在拜訪的數值相加後反而比正在拜訪的數值還小徑應該捨棄前面的累加，從新以目前拜訪的數值開始累加。另外每更新一次累加後就應該更新global maximum。

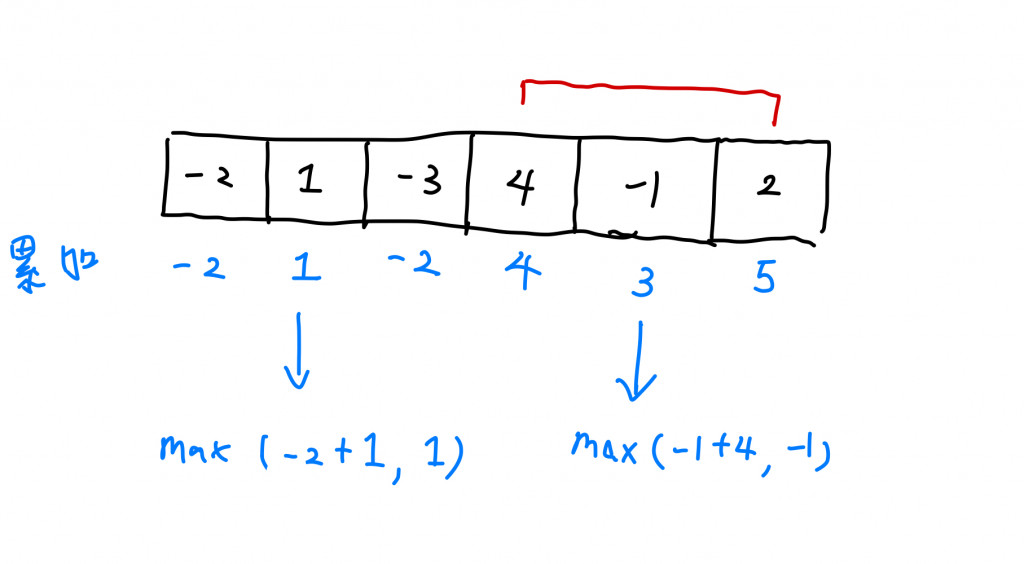
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        globMax = nums[0]
        curSum = 0

        for n in nums:
            curSum = max(curSum + n, n)
            globMax = max(globMax, curSum)
        
        return globMax

Leetcode 152. Maximum Product Subarray

和上一題不一樣的地方在於這次比較的方式是乘法。要注意的是我們這次必須去紀錄每一段subarray的最小值，因為若是目前拜訪度數字為負數，之前累積的最小值與之相乘可能會反轉成最大值；相反的最大值也可能會反轉成最小值。

Example:

Input: nums = [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.

以Python實作：

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        globMax = nums[0]
        curMax, curMin = 1, 1

        for n in nums:
            tmpMax = max(curMax * n, curMin * n, n)
            tmpMin = min(curMin * n, curMax * n, n)
            curMax, curMin = tmpMax, tmpMin
            globMax = max(globMax, curMax)
        
        return globMax

Leetcode 32. Longest Valid Parentheses

這是今天的最後一題，辛苦看這篇文章的朋友們了。這題的難度是Hard，但只要考慮到所有的情況加上如果是用Python解題的話，程式碼不到20行就可以解出來。

題目敘述：
有一個由字元'('和')'所組成的字串，找出最長的有效substring。這裡的有效指的是每個左括號會有一個右括號與之對應。

Example1:

Input: s = "(()"
Output: 2
Explanation: The longest valid parentheses substring is "()".

Example2:

Input: s = ")()())"
Output: 4
Explanation: The longest valid parentheses substring is "()()".

分析：

• 當我們遇到右括號時才會去尋找與之對應的左括號，所以在此之前我們需要將左括號都存起來，這時候就可以利用stack來儲存，因為stack先進後出的特性，右括號會先和離他最接近的左括號配對，這樣就算是一個合理的pair。
• 我們用dp[index]來代表在包含這個index之前最長的有效substring的長度。
• 我們將左括號存入到stack時，會存入tuple (左括號, index)
• 為什麼要存入index? 因為index左側即index - 1可能是「一段有效的substring的終點」
• 考慮右括號的前一個index，因為s[index - 1]也是一個右括號的話代表他們裡面也有「一段有效的sub-sub-string」

示意圖：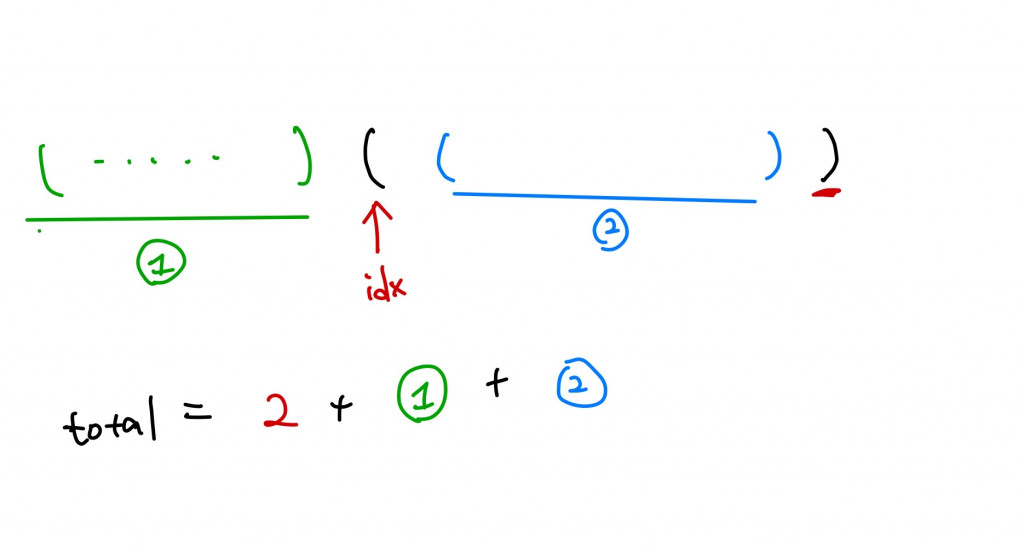

程式碼：

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        stack = []
        dp = [0 for _ in range(len(s))]
        globMax = 0

        for i in range(len(s)):
            if s[i] == "(":
                stack.append((s[i], i))
            elif stack:
                _, idx = stack.pop()
                if idx > 0:
                    dp[i] = dp[idx - 1] + dp[i - 1] + 2
                else:
                    dp[i] = dp[i - 1] + 2
                
                globMax = max(globMax, dp[i])
        
        return globMax

後記：如果你只收到心中第三志願的公司的offer，其他第一志願和第二志願還在面試，但是主管已經要你決定要不要來上班了，你會去嗎