昨天我們談到若要使用機器學習來解決一個問題，會需要經過三個步驟

1. 定義函數
   定義出模型的架構，如：
2. 將資料輸入進模型，並評估模型好壞
   透過評估模型的好壞，接下來就能夠知道怎樣調整會比較好。
3. 調整參數大小
   依據評估調整參數。

而在上一篇文章我們知道可以透過一些多項式來定義函數，或是改成使用矩陣、向量的形式，讓表達上會更加簡單且更具擴充性。後續也提及使用 Loss Function 去評估一個模型的好壞。今天就要來談談最後一個步驟，調整參數大小。

在參數更新之前

讓我們回到第二天的這張圖。假設我們的模型十分簡單，只是單純的 。當中只有兩個可以調整的參數 。
至於評估模型的方法，我們就先使用 MSE 吧！

雖然說我們有 Loss Function 可以去評估一個模型整體的好壞，但是顯然如果只有一個數字，我是不知道該如何對 去更新的。不過我們知道 Loss 越高意味著模型越糟，所以我們的目標總是希望Loss 越低越好。

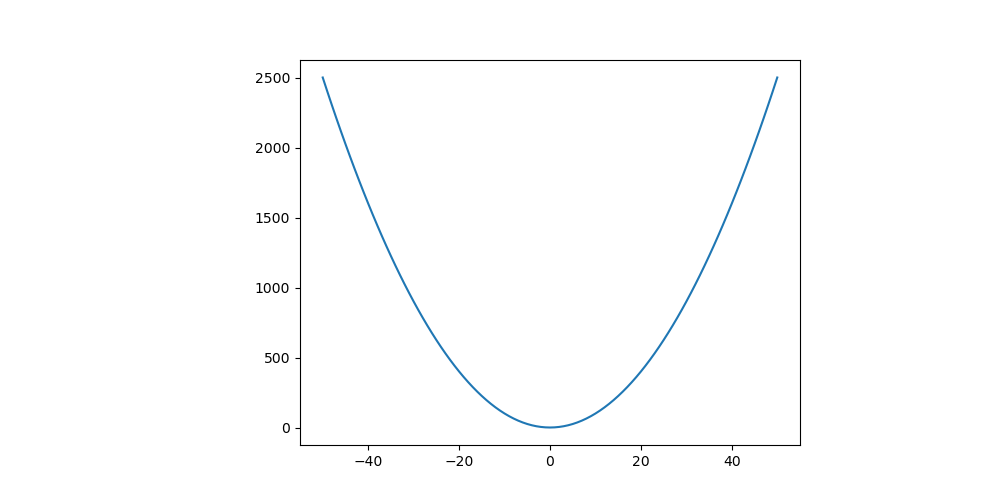
如果 Loss Function 是一個二維的曲線如下圖單純的 ，那麼我們會知道 Loss 最低的地方會是在 的地方。為什麼呢？因為它是整個函數的最小值。

如果 Loss Function 的維度再高一點如下圖，黑點表示某個時間點下模型的 Loss，而移動的過程就是試圖去找到 Loss 的最低點。

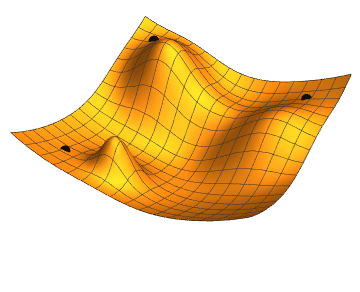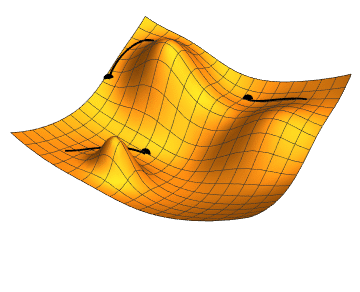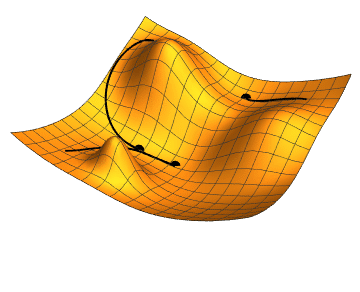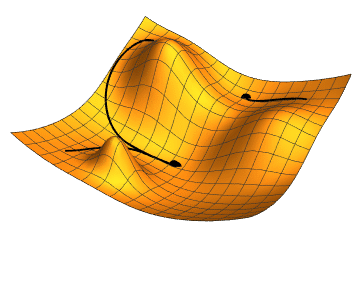
Source From Jacopo Bertolotti, CC0, via Wikimedia Commons

從上面兩個觀察可以發現到，這個"最低點"有個特色是周圍的點都比他還要高。所以如果要走到這個低點，肯定是從比較高的地方走過來的對吧！

Source From Ken Lund, CC BY-SA 2.0, via flicker

這個更新的過程就跟下山是一樣的。我們會從比較陡峭的地方，慢慢地往低的地方前進，直到我們走到了平地。

• 陡峭，意味著斜率大。
• 平地，意味著斜度為 0

更新參數的目標，是從斜率大的地方移動到斜率小的地方。

假如現在所在的點斜率是負數，如下圖。那麼我們應該要往正的方向移動。否則我們是在上山而非下山。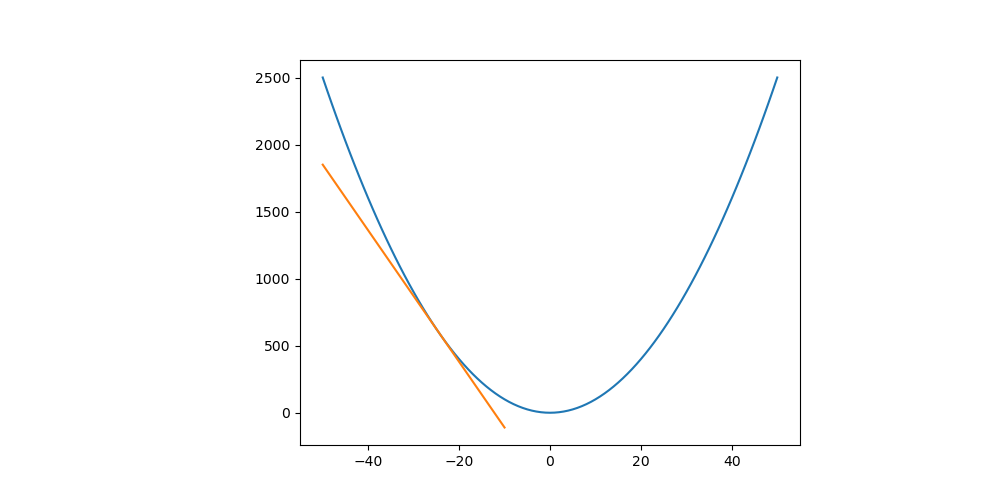

假如現在所在的點斜率是正數，如下圖。那麼我們應該要往負的方向移動。否則我們是在上山而非下山。

更新都是往斜率的負方向前進

梯度下降法

這種更新參數的想法被稱為 梯度下降法(Gradient Descent) 。
對於每一個參數，我們都想知道它對 Loss 造成怎樣的影響，而它應該要往正方向更新，還是要往負方向更新。因此這裡要做的會是偏微分而非微分，找到 分別造成的影響。

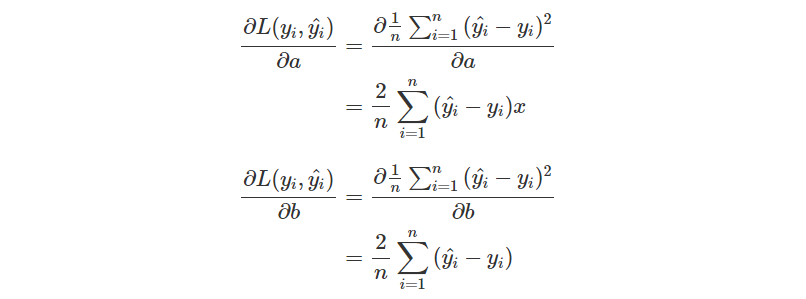
也因為這樣的 Loss Function 定義會導致前面留下一個倍率 2，所以很多時候會看到的 MSE 定義會多乘上 。

當我們能夠求出偏微分，那就可以往負方向去更新參數了。此外，我們還會定義一個 學習率(Learning Rate) 來調整"步伐"，也就是一次要跨多大步。因此更新就會變成。

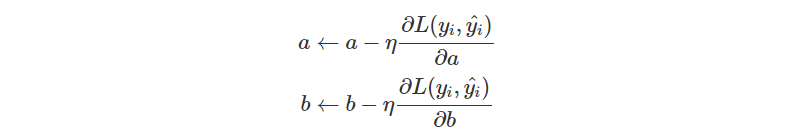
重複幾次這樣的操作，更新後再次評估模型，再次更新參數，直到你覺得這個模型足夠好，或是已經不能繼續更新時，那就可以停下來了！

總結來說，今天我們看到更新參數其實就是希望讓 Loss Function 斜率能下降到 0，而如果希望往斜率小的地方移動，應該要往斜率的負方向去更新。
不過因為我們有兩個參數，需要分別去看這兩個參數對 Loss Function 造成的影響，因此會需要做偏微分來找到答案。

在下一篇文章我們會實際上帶大家走過如何寫下第一個 Linear Regression with Gradient Descent 的程式！