• 課程網址
• 哪個視覺模型最好? notebook
• 神經網路是如何運作的? notebook

前面幾堂我們得到了model.pkl
那我們會想說我們練出來的模型，夠好嗎?
之前上課老師說為了快速，用了一個比較快的又小的模型

那有沒有比較大，比較慢，又厲害的模型呢?
比較大一定就厲害嗎?
這時，就可以看置頂的「哪個視覺模型」最好這個notebook
有一張圖可以顯示，x軸是時間，y 軸是執行效果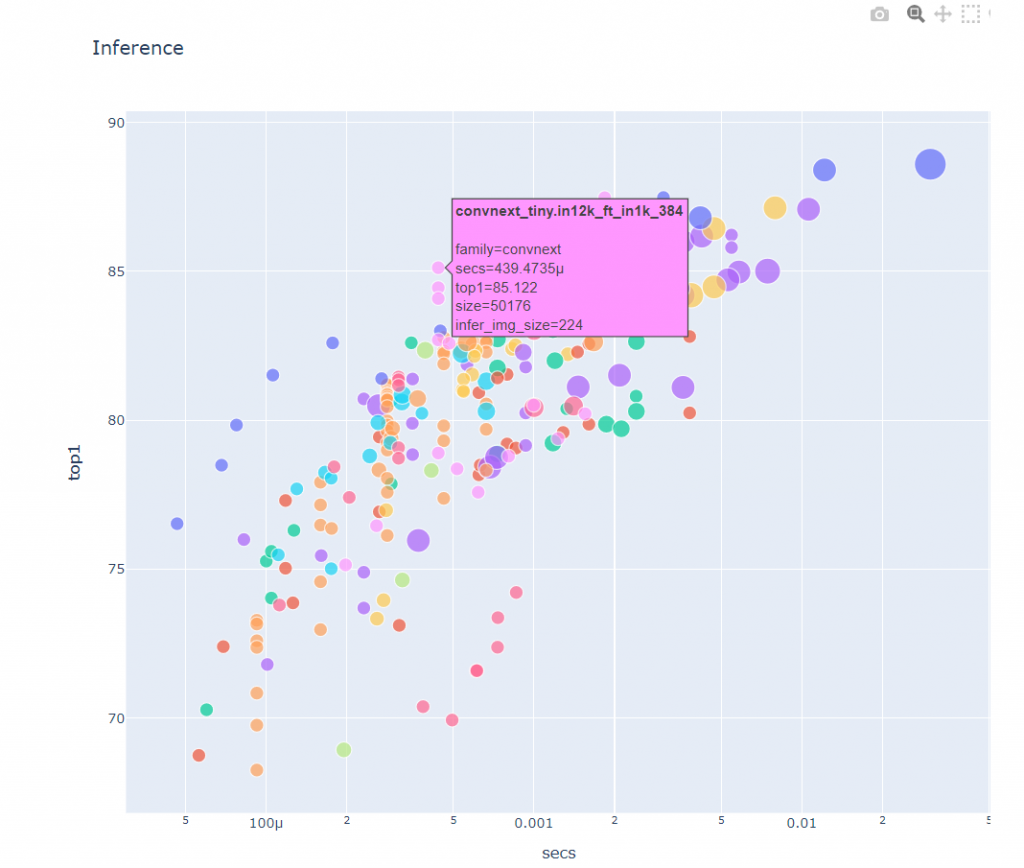

哇賽這麼多模型學都學不完
那我們就會想，這些模型是怎麼被做出來的?
這些模型都有論文
但我們直接看論文也太難
所以我們先從了解神經網路入手

神經網路也是一種機器學習，在了解神經網路前
我們先了解一下機器學習的概念

機器學習就是經過數據，所整理出來的一套邏輯
就像我觀察要離職的同事，在離職前「通常」會「一直請假」，因為他們要去面試
所以我把這種「一直請假」的行為，「歸類」在「離職」
這種推理過程，寫成程式就是一種機器學習

用視覺化的方法來呈現
假設我們有一個方程式，可以畫出一條線
這個線有什麼特別的呢?
就是你只要有一個x 值，你就能算出他的y值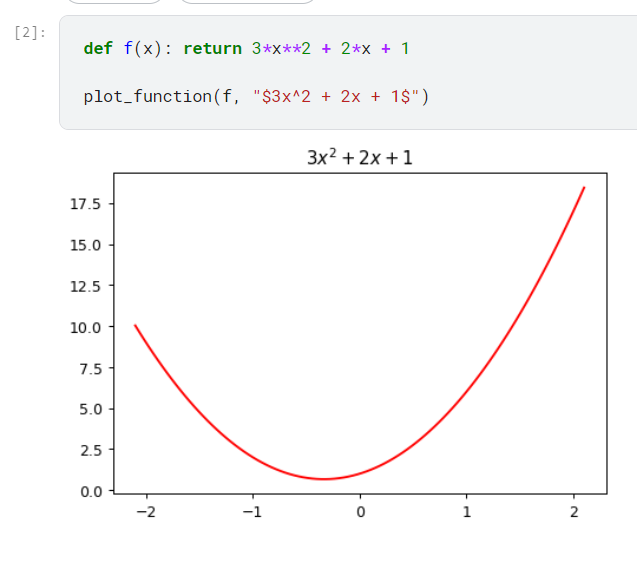

在這條線的週圍，我們隨機產生一些點，看看神經網路能不能幫我們找出一條最接近的線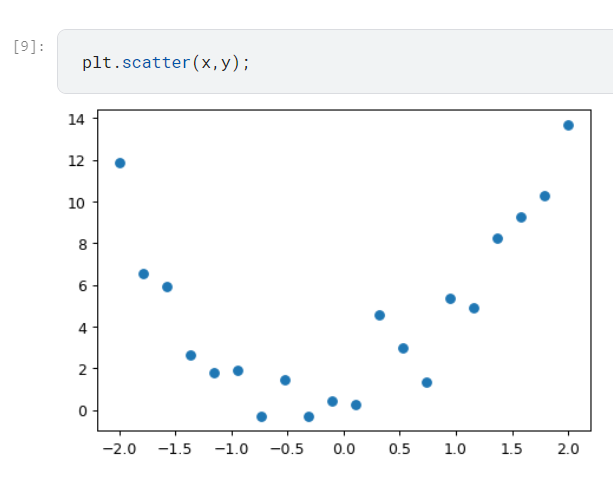

好，那我們把神經網路擬人化，我們假裝自己是神經網路
假設神經網路已經知道是2次多項式，他可以做的事情就是把線扭來扭去
移來移去，看看能不能讓所有的點最接近原來的線
這邊加了一個裝飾器，讓我們可以自由調整下面的abc三個參數
記得要「run」這個notebook 才能拖動哦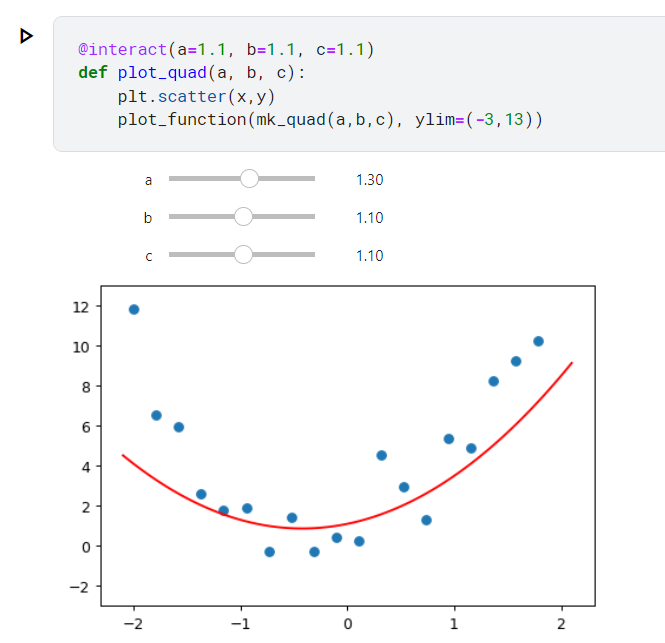

那什麼叫做「最接近」呢?
所以我們需要定義一個方法來計算。

我們可以定義在我們的線，距離真正的y值差距多少，取平均值來定義這個模型的好壞
我們有10個點，就取10個點的誤差，這個取絕對值平均的方法叫做
mae ，這個公式就是我們面對這個問題的loss function
所以我們把mae 加入互動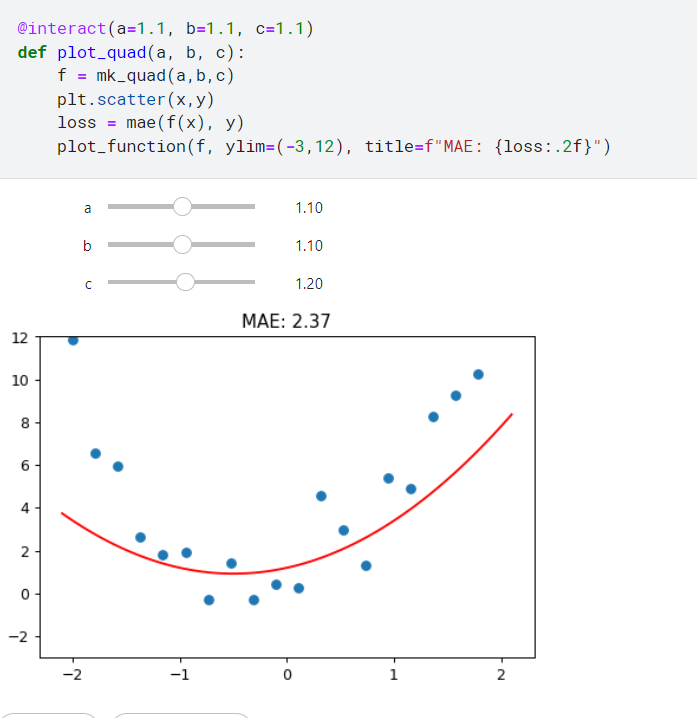

題外話
在現實世界我們要解決一個問題，可以自己定義一個方式來評估，不同的loss function會有不用的效果
但有時候也有可能根本就定錯loss function
但如果是打比賽的話，就會有固定的loss funtion ，大家以此為標準來競賽

現在我們要想的是，我們手動在那邊拖來拖去，這樣怎麼讓程式自已運作?
我們在圖上拖1下的最小單位是0.1
可不可以更小一點呢?0.001, 0.0001 ?
這個一次「動」的大小，就是我們所謂的學習率(learning rate)
我們因為有「視覺」的關係，所以可以知道一口氣要拖到哪裡比較「剛好」
我們的策略是先拖到「差不多」的位置
再來→調大→調小
電腦做這件事的時候，他只有loss function
所以他是個瞎子
所以learning rate 的調整策略，也是優化中很重要的一環
調太大容易怎麼調都調不好
調太小就會跑太久

那我們總不可能每次都在那邊拖來拖去吧
而且參數一多，也不是拖來拖去就可以解決的

還好寫程式可以幫我們解決這個問題
那剛才提到的策略 ，我們總要知道朝著哪個方向「前進」才是對的吧
所以這時候就要用到微積分了
經過偏微分我們可以很好的理解這個問題
你以為接下來要出現數學式了嗎?

這堂課清楚的說只用到高中數學，所以超過這個限制就是自打嘴巴!

剛才有講到，咦我們怎麼知道下一次要調大還是調小，我們的「方向」有對嗎?
我怎麼知道下一次對比前一次的結果，是離目標近還是遠?
我現在是在往哪個方向走?
好了我們不講數學，只講一個方向性，這邊用「梯度」來代表

如果某個參數的梯度是正的，就是說在當前參數值的設定中，如果我們稍微增加該參數，損失函數的值也會增加。這表示我們當前的參數值可能過大，導致損失函數的值不斷增加。

如果某個參數的梯度是負的，意味著在當前參數值下，如果我們稍微增加該參數，損失函數的值會減少。這表示我們當前的參數值可能過小，導致損失函數的值不斷減少。

梯度的方向指示了最陡峭上升或下降的方向。根據梯度的方向，我們可以采取相應的步驟來更新參數，以便逐漸降低損失函數的值。通常，梯度下降算法會將參數朝著梯度的反方向進行微小的調整，以最小化損失函數。這是因為我們的目標是使損失函數的值尽可能小。所以，正的梯度值表示當前參數值過大，需要減小參數；負的梯度值表示當前參數值過小，需要增加參數，以便使損失函數更小。

說那麼多還不如實際寫個程式操作一下

def quad_mae(params):
    f = mk_quad(*params)
    return mae(f(x), y)

上面這段程式接受参数 a、b 和 c 的输入，並基於這些參數計算 mae() 的值。然後，我們可以找到 mae() 對於每個參數的梯度，然後按照梯度的相反方向微調參數，以逐漸降低 mae() 的值。這就是優化函數的基本思想。
中間過程，在notebook中都有，就不再提

for i in range(10):
    loss = quad_mae(abc)
    loss.backward()
    with torch.no_grad(): abc -= abc.grad*0.01
    print(f'step={i}; loss={loss:.2f}')

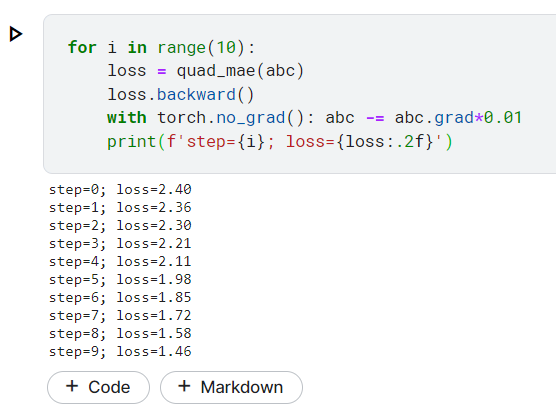
這邊可以看到執行結果，我們只執行10次，可以看到在過程中loss 慢慢變小!

這邊只是一般機器學習的內容，顯然神經網路能做的事不是只有這麼一點，他能根據數據學到更多東西，
那有關神經網路怎麼「學到」東西，我們明天再說