Adjacency Matrix

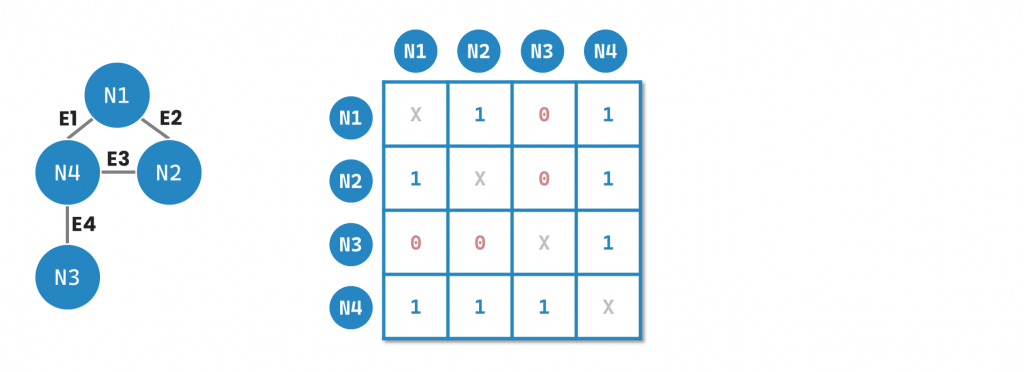
最基本儲存圖的資料結構叫做 Adjacency Matrix 是一個 的二維陣列，假如節點跟節點之間有邊連接就填入 1（或是權重的值）；其餘就填入 0。它的優點在於簡單、好懂、新增或是刪除邊很方便。缺點就是占據非常大的空間 ，尤其是整個圖中的邊不多，二維陣列裡面就會有很多 0。

所需空間：
時間複雜度（確認節點之間有沒有連結）：
適用場景：稠密圖、有向以及無向圖

Sparse Matrix

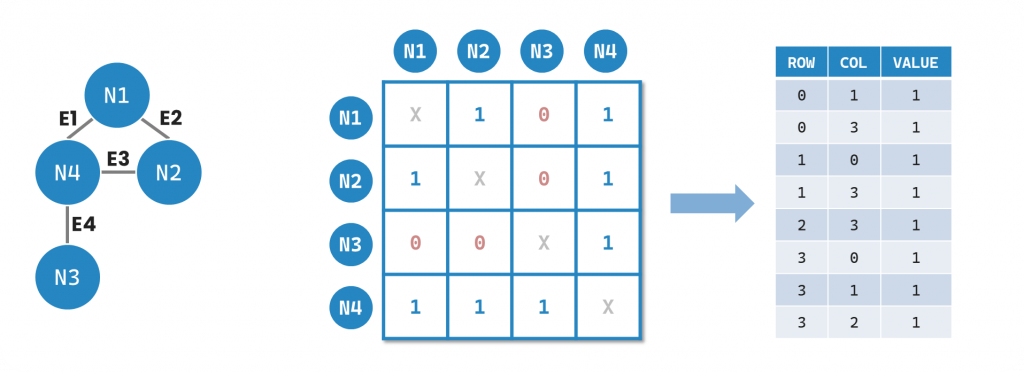
有鑑於 Adjacency Matrix 不適合太過稀疏的圖，因此引申出一種新的資料結構稱為 Sparse Matrix，這種資料結構只會保存有邊的資料。

所需空間：
時間複雜度（確認節點之間有沒有連結）：（可用二分法）
適用場景：稀疏圖、有向以及無向圖

Adjacency List

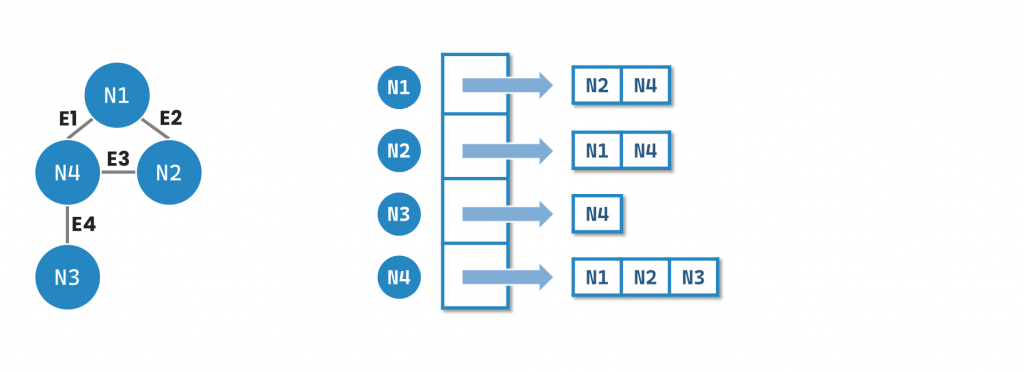
Adjacency List 是一種以每個節點作為鍵（key），並與其相連的節點列表作為值（value）的資料結構。每個節點的鍵（key）對應到一個 list，其中包含與該節點相連的其他節點。

所需空間：
時間複雜度（確認節點之間有沒有連結）：
適用場景： 稀疏圖、有向以及無向圖

Incidence matrix

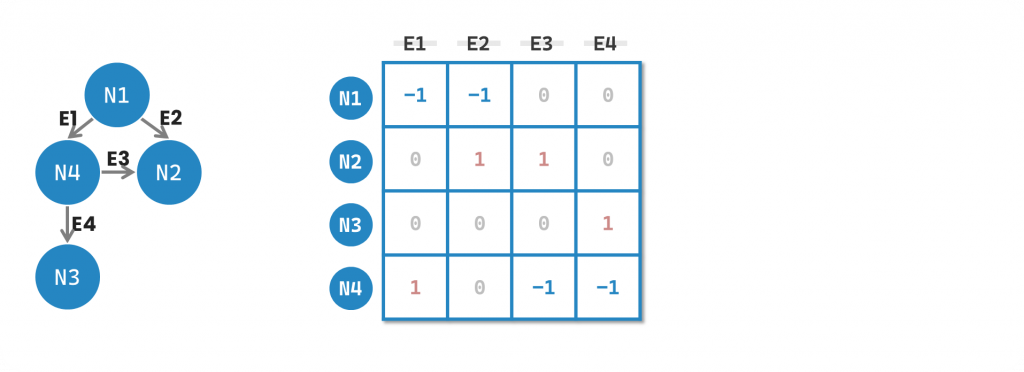
橫向為節點以及縱向為邊的資料結構。裡面的值為 -1, 0, 1，代表該邊是由該節點往外指向其他節點、沒有邊或是指向該節點。

所需空間：
時間複雜度（確認節點之間有沒有連結）：
適用場景： 稀疏圖、有向圖

參考資料

• Graph Data Structure And Algorithms
• Adjacency matrix meaning and definition in DSA
• Graph Representation: Edge list, Adjacency Matrix, and Adjacency lists
• Data Structures Tutorials - Sparse Matrix with an example
• Comparison between Adjacency List and Adjacency Matrix representation of Graph
• What is Incidence Matrix?
• Incidence matrix instead of adjacency matrix