了解到可以使用哪些資料結構儲存圖之後，接下來的第一步就是了解這個圖的性質。也就是資料分析的第一步，了解你的資料集。
下面提供了幾個常見的 network properties，讓各位在拿到資料集之後，可以先用這些 properties 來了解這個圖的基本資訊。
例如，可以計算圖中的節點數量、邊數量、平均度數等。我的邏輯是先從小到大，從 node 開始，再到 edge，最後到整個 graph 的結構。
| Property | Description |
|---|---|
| Node In-Degree | 指向該節點的連接數量 |
| Node Out-Degree | 節點指向其他節點的連接數量，較高的 Out-Degree 代表該節點在圖中有較多的影響力 |
| Node Degree Distribution | 在圖裡面所有節點 Degree 的分佈狀態，顯示出網絡中節點度數的分布模式，例如是否符合 Binomial distribution 等... |
| Average Node Degree | 所有節點的平均 Degree，反映出整個圖裡面所有節點的連接程度 |
| Maximum Node Degree | 所有節點中最大的 Degree |
| Minimum Node Degree | 所有節點中最小的 Degree |
Diameter 是指圖中『最長的最短路徑』，也就是圖中兩個節點之間最遠的距離。
藉由計算途中所有節點之間的最短路徑，並取平均值，來了解整個圖的平均路徑長度。
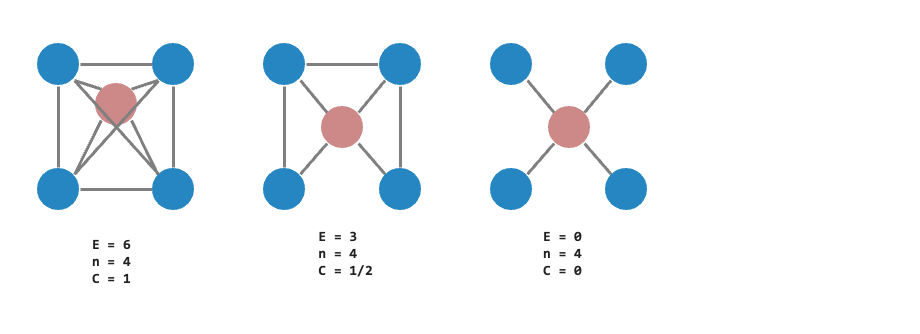
主要是計算單一個節點與其鄰居節點之間的連接緊密程度。
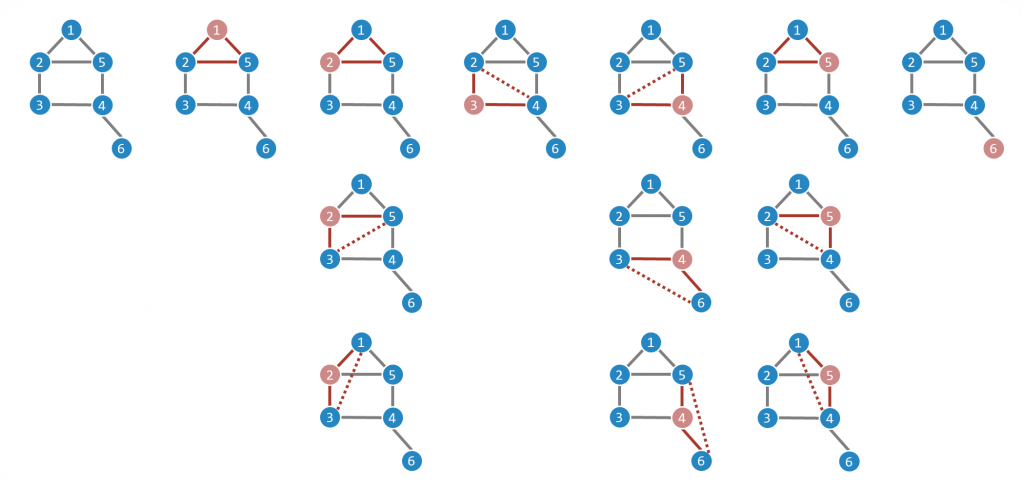
主要是用來衡量整個網絡中聚集程度的指標。它衡量了網絡中形成三角形的程度，也可以理解成在所有三元組（由三個節點組成，它們之間有兩條連接，triplets）中形成封閉三角形的機會。
描述網絡中是否存在孤立的部分，簡單來說就是圖中的所有節點是否都可以連通
描述網絡中形成三角形結構的程度
描述網絡中節點度的異質性，即度分佈的不平均程度
描述網絡中常見的小型拓撲結構或模式，例如三角形、四方形等
iThome鐵人賽
看影片追技術